The True Atom

{Keith Dixon-Roche © 17/04/18}

This webpage provides the evidence that a Newtonian atomic model can mathematically predict any property of any and all atoms simply from its atomic number, and thereby renders Quantum Theory unnecessary.

Sources: Planck's Atom; Newton's Atom; Laws of Motion; Physical Constants
Related Books: Philosophiæ Naturalis Principia Mathematica Rev. IV; The Atom; The Mathematical Laws of Natural Science
Related Calculators: Atomic Elements; Orbital Motion; Atoms; Physics
CalQlata comment: This is the only study we (at CalQlata) know on this subject that manifestly works.

Introduction

The purpose of this study is to answer the following question:
1) Can the Newtonian atomic model be used to predict its properties simply from its atomic number?

Conclusion

The answer to the above question is yes, albeit input from Coulomb, Rydberg and Planck was required to complete it.
Calculators based upon this atomic model are now available (see Sources above) that predict the density of matter (viscous and gaseous), EME spectrum (at any temperature), gas transition temperature and specific heat capacity of all 92 natural atoms simply from their atomic numbers. When considered together with its ability to predict the noble gas atoms, and alternative calculation methods for PVRT and Drag, along with the verification calculation example (below), this (Newtonian) model must be declared correct and that the Quantum model, which cannot, must be declared redundant.

The Model

The atom is simple, elegant and a brilliant piece of engineering. Whilst all the information needed to understand it was available at the end of the 19ᵗʰ century, a total appreciation of its qualities has continued to elude us.

An atom is a collection of proton-electron pairs, each with one or two neutrons attached and their electrons orbiting in equally-spaced circular shells.
Each electron shell contains two electrons - orbiting opposite each other - except the outer shell which may contain one or two electrons, dependent upon atomic number. During electrical transfer, the outermost electrons (with the lowest potential energy) are always removed. If an inner electron is knocked from its shell, all the outer electrons will relocate inwards to fill the resultant valence. There are no shell valences; all potential forces must balance.
Every proton, neutron and electron in every atom is identical to every other proton, neutron and electron in the universe, and obeys Newton's laws of orbital motion, Coulomb's force law and spin theory.
Full-stop. That's it. Nothing more.
Simple isn't it!
But the fact is, it works. This model can mathematically predict all the properties of every atom at any temperature. So, it must be correct.

Atomic Structure

An atom is a collection of identical electrons, identical protons and identical neutrons. They are arranged as unique proton-electron pairs each of which possesses one or two neutrons that are held by the magnetic field force generated by the proton-electron pair.
Each electron is orbiting its proton partner; not the atomic nucleus. The collection of proton-neutron partnerships are inside a collection of electron shells only because they have been forced there by fusion inside a cold body (at the temperature of outer space) with sufficient internal gravitational force, such as galactic force-centres, the Great Attractor and the ultimate body.
The higher a proton-electron pair's temperature, the greater the build up of electrical charge (e') in its proton - provided by its orbiting electron partner - drawing the orbiting electron closer to its proton partner; reducing its orbital radius and strengthening the atom.
However, the electrical charge generated in the proton will also rise with increasing temperature. When this repulsive force exceeds the magnetic field force the atoms will exist as a gas.

Electron Shells

Each electron shell contains two electrons - except the outermost shell which can hold one or two electrons dependent upon atomic number - both of which are identical.
All the electrons are held in their shells by a balancing act between mutual electrical repulsion, and attraction to their proton partners in exactly the same way as Newton described the balance between centrifugal force and gravitational force in an orbiting satellite and its force-centre.

Shell radii are calculated thus:
Note: suffix '₁' refers to the electrons in the innermost shell (shell-1) & suffix 'ᴺ' refers to all the other electrons according to their shell number (shell-N)
R₁ = XR.Ṯ₁
Where;
Ṯ₁ is the measured temperature of the atom
Rᴺ = R₁.N
Ṯᴺ = XR/Rᴺ
vᴺ = √[Ṯᴺ/X]
KE = ½.mₑ.v²
PE = -2.KE

The electro-magnetic energy (EME) absorbed by the orbiting electrons, or lost to their surroundings, alters their kinetic energy according to their shell-number.
Orbiting electrons continuously collect electro-magnetic energy (heat) converting it into kinetic energy (increasing their velocity). In doing so, proton-electron pairs generate (and radiate) electro-magnetic energy, simultaneously reducing kinetic energy in the electrons.
Electron performance in any shell can be calculated using the formulas provided in the proton-electron pair web-page.

Atomic Nucleus

The nucleus of an atom comprises the proton partners of the proton-electron pairs that populate it, along with their attached neutron(s) that may be one or two per proton-electron pair.
The structural arrangement of the nucleic protons and neutrons will define the atomic lattice structure in both gaseous and viscous conditions.

The proton-neutron populations define their neutronic ratio (ψ), which may theoretically range between 1.0 and 2.0
Note: each proton electron pair within an atom is either a deuterium atom (1.0) or a tritium atom (2.0).
In practice, however, as soon as an atom's neutronic ratio exceeds 1.6, the atom will spontaneously split into smaller atoms, with smaller atomic numbers.
Atoms close to this neutronic ratio (ψ) will spontaneously and continuously eject two neutrons splitting both into their component parts; an electron and a proton.
If after splitting into its component parts the proton cannot escape its nucleus, the proton-electron pair will instantly release its stored energy in the form of electro-magnetic energy (heat) and the atom's atomic number will increase by one.
If on the other hand the proton does escape its nucleus, the component parts will be released as an alpha particle and a beta particle, at a velocity commensurate with the energy released.

The proton force-centres, and their neutron partners, do not sit together as a single entity inside an atom, their common positive charges prevent this from occurring. Having been forced inside a common shell structure due to fusion, they arrange themselves inside the innermost electron shell(s) balancing their common repulsion with their attraction with the orbiting electrons.
The settlement of these protons (and neutrons) at their lowest energy level is what creates each unique nucleic structures, which they replicate in the relative atomic (lattice) structures in matter.

Atomic Strength

As orbiting electron velocities increase with rising temperature, their orbital radii decrease owing to the increased electrical charge collected and retained by their proton partners, which increases the potential energy in the proton-electron pairs, thereby increasing the strength of the atoms in which they reside.
I.e. the strength of an atomic assembly rises with increasing temperature.
The relationship between proton electrical charge and temperature may be calculated as follows:
e' = mₚ.RC/c . √[Ṯ/X]
However, this same increase in proton electrical charge drives adjacent atoms apart (Fig 2), see The State of Matter.

Isotopes

Isotopes are atoms with the same atomic number (Z) but with varying atomic mass due to unequal proton-neutron pairing.

For example; an atom of iron, with 26 protons and 26 neutrons is an isotope of 52. However, in nature, most iron atoms have more than 26 neutrons, each of which is given its own isotope, e.g. 57, 59, etc.

Over time, neutron-neutron interaction will cause neutrons to separate into their component parts (a proton and an electron). Some of these separations will result in an atom retaining its proton-electron pair and increasing its atomic number, releasing heat, and others will escape the nucleus as alpha and beta particles. The rate at which this occurs is referred to as the half-life of the atom. The half-life of any atom is a constant, it never changes.

Apart from oxygen all atoms naturally have more neutrons than protons.

Ions

Ions are atoms with the same atomic number (Z) but possess an electrical charge due to unequal proton-electron pairing.

Positive ions (atoms that have lost electrons) possess a positive electrical charge. Negative ions (atoms with additional electrons) possess a negative electrical charge. Negative ions are far less common than positive ions.

Only a few atoms exist naturally as negative ions and they are all non-metalsN except for two, which are semi-metalsS:

One additional electron (Group VIIA):
Fluorine (9N), Chlorine (17N), Bromine (35N), Iodine (53N)

Two additional electrons (Group VIA):
Oxygen (8N), Sulphur (16N), Selenium (34N), Tellurium (52S)

Four additional electrons (Group IVA):
Carbon (6N), Silicon (14S)

Any atom can become a positive ion simply by losing one or more of its electrons from impact with free electrons or a strong external positive electrical charge.

Negatively charged ions are a little more difficult to understand. Additional electrons need to be trapped by the positive charge in protons that do not exist in the nucleus, which shouldn't be possible. However, the nucleic structures of the above non-metal atoms probably have at least one exposed proton that is not protected by a neutron, giving its additional electrical charge (e') the ability to trap passing free electrons

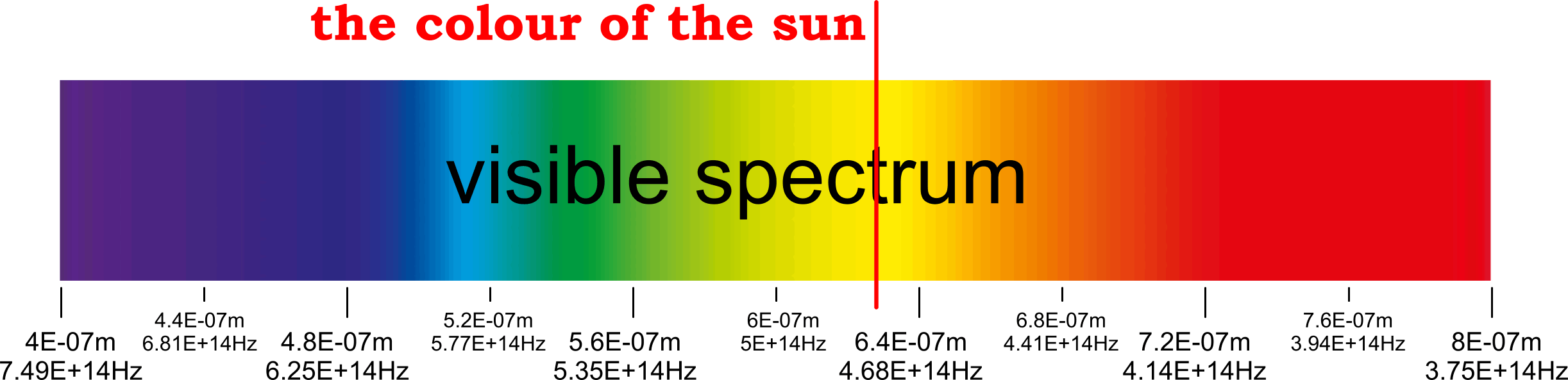
Our Sun's Colour

The surface temperature of our sun is said to be about 5778K, which would be impossible if the sun's surface comprised lone protons that cannot collect or emit electro-magnetic energy (i.e. heat or colour). And according to the atomic model:
KE = 3.7493802154296E-19 J
electron velocity = 912757.252 m/s
at an orbital radius of 3.03992067E-10 m
ƒ = v / 2πR = 4.77873747733E+14 Hz
λ = c/ƒ = 6.2734657516211E-07 m

Electron Shells

The following calculations define the performance of the orbiting electrons in an iron atom at 300K (Ṯ₁ = 300K)

Nº	Ṯ	R	v	g	KE	PE	F	h	K
1 2 3 4 5 6 7 8 9 10 11 12 13	300 150 100 75 60 50 42.86 37.5 33.33 30 27.27 25 23.08	5.86E-09 1.17E-08 1.76E-08 2.34E-08 2.93E-08 3.51E-08 4.10E-08 4.68E-08 5.27E-08 5.86E-08 6.44E-08 7.03E-08 7.61E-08	208000 147100 120100 104000 93010 84910 78610 73530 69330 65770 62710 60040 57680	7.39E+18 1.85E+18 8.21E+17 4.62E+17 2.96E+17 2.05E+17 1.51E+17 1.15E+17 9.12E+16 7.39E+16 6.11E+16 5.13E+16 4.37E+16	1.97E-20 9.85E-21 6.57E-21 4.93E-21 3.94E-21 3.28E-21 2.82E-21 2.46E-21 2.19E-21 1.97E-21 1.79E-21 1.64E-21 1.52E-21	-3.94E-20 -1.97E-20 -1.31E-20 -9.85E-21 -7.88E-21 -6.57E-21 -5.63E-21 -4.93E-21 -4.38E-21 -3.94E-21 -3.58E-21 -3.28E-21 -3.03E-21	-6.73E-12 -1.68E-12 -7.48E-13 -4.21E-13 -2.69E-13 -1.87E-13 -1.37E-13 -1.05E-13 -8.31E-14 -6.73E-14 -5.56E-14 -4.67E-14 -3.98E-14	0.001218 0.001722 0.002109 0.002435 0.002723 0.002983 0.003222 0.003444 0.003653 0.003851 0.004039 0.004218 0.004391	0.1558788 0.1558788 0.1558788 0.1558788 0.1558788 0.1558788 0.1558788 0.1558788 0.1558788 0.1558788 0.1558788 0.1558788 0.1558788
Electron Performance in an Iron Atom @ 300K

The following calculation results define the performance of an orbiting electron that has achieved light speed

Ṯ	R	v	g	KE	PE	F	h	K
6.233E+08	2.818E-15	299792459	3.189E+31	4.094E-14	-8.1870E-14	-29.0544	8.4480E-07	0.1558788
The Birth of a Neutron

Whilst the above description and formulas are sufficient to analyse any atom at any temperature, the following reference publications provide considerably greater detail to that provided above.

Verification

In conclusion (see below), the Newton/Coulomb atomic model must be correct.

The Boiler

By way of verification, we can apply this atomic model to a practical example, say; the performance of a domestic boiler.
One well known manufacturer claims the following for one of its models, rated at 30.5kW input energy:
Option 1: at 12.1 litres per minute it generates a temperature rise of 35°C
and;
Option 2: at 14.1 litres per minute it generates a temperature rise of 30°C

Using the above atomic model together with the proton-electron pair:
A water (H₂O) molecule has a mass of 3.01201E-26 kg and contains 8 proton-electron pairs, therefore;
at 283K (≈10°C); ΣKE = 3.87201945657701E-20 Joules (per molecule)
at 313K (≈40°C); ΣKE = 4.28248088306927E-20 Joules (per molecule)
at 318K (≈45°C); ΣKE = 4.35089112081798E-20 Joules (per molecule)
Half the kinetic energy in the orbiting electrons is emitting EME and half is holding on to the [2] hydrogen atoms.

Option 1: 283K to 318K
water mass = 12.1kg/min or 4.01725214286213E+26 molecules/min, giving the following EME (heat) energy emission:
½.ΣKE₁ = 15554878.459138 Joules at 283K (10°C)
½.ΣKE₂ = 17478626.678466 Joules at 318K (45°C)
E = ½.(ΣKE₂-ΣKE₁) = 1923748.2193 Joules
power = E/60 = 32062.47032 Watts (32.062kW)

Option 2: 283K to 313K
water mass = 14.1kg/min or 4.68126076151703E+26 molecules/min, giving the following EME (heat) energy emission:
½.ΣKE₁ = 18125932.7499044 Joules at 283K (10°C)
½.ΣKE₂ = 20047409.719859 Joules at 313K (40°C);
E = ½.(ΣKE₂-ΣKE₁) = 1921476.969955 Joules
power = E/60 = 32024.61617 Watts (32.025kW)

The above calculations represent a theoretically perfect condition in which every molecule passing through the boiler achieves the correct temperature rise, which is impossible. It is expected, therefore, that some of the water passing through the boiler must be at a slightly lower than expected temperature. Whilst the power required to raise the temperature of every molecule of water is predicted as 32kW, the actual power (allowing for some slightly cooler molecules) of 30.5kW is considered reasonable. Moreover, the predicted (calculated) efficiency (92.3%) relates very well to the manufacturer's claim (90%).

Carbon Dating

All atoms continuously decay in their aim to reach a neutronic ratio of 1.

The rate of decay of all atoms is constant (its half-life) dependent upon neutronic ratio, but they always decay as neutron pairs because neutrons are always created in pairs. The two innermost proton-electron pairs are always at the same temperature and will therefore unite simultaneously.
This is why radioactive decay is described as the emission of helium atoms; two alpha particles and two beta particles and/or the emission of heat.

If both protons escape - emitting two alpha particles and two beta particles - the atomic number will remain unchanged, but the neutronic ratio will reduce thus; (RAM-2)/Z - 1 making the atom more stable. It will remain as such for longer.
If one proton escapes the nucleus emitting one alpha particle and one beta particle, the other neutron will revert to a proton-electron pair (releasing its stored energy as heat) and the atomic number will increase by 1.
If neither proton escapes the nucleus, the atom will increase its number by 2 releasing their stored energy as heat.

The carbon-12 atom is stable because it has a neutronic ratio of 1. It does not decay further.

Carbon-14 has a neutronic ratio of 1.333, which means it is unstable; it will decay - at a constant rate - relatively quickly; thousands of years, as opposed to millions (or billions) of years. This is why carbon can be dated with relative surety.
Carbon-14 decays by losing two neutrons simultaneously, one of which will be lost to the atom as an alpha and a beta particle. And the other is retained as a proton-electron pair, releasing its stored energy as heat. This process will result in the decay of carbon-14 to nitrogen, with a neutronic ratio of 1, making it stable.

This means that other atoms, even metals, should also be dateable using the same reasoning (technique).

Simple Logic

Whilst the validity of the Newton Coulomb atomic model has already been demonstrated using; a domestic boiler, PVRT, the state of matter, electricity, etc., that this is the correct atomic model is beyond doubt comes simply from the incontrovertible prediction of an indisputable pre-twentieth century constant (kB) using the potential energy in a proton-electron pair.
The kinetic energy of an electron in a proton-electron pair varies with the EME it absorbs from its surroundings thus:
KE = ½.mₑ.v²
v² = Ṯ/X
and the potential energy in circular orbits is always twice the satellite's kinetic energy:
PE = 2.KE = 2 . ½.mₑ.v² = mₑ.v²
but also:
PEₙ = mₑ.c²
kB = PEₙ / Y.Ṯₙ = PE/Y
at any specified temperature (Ṯ), the potential energy in the proton-electron pair is:
PE = Y.kB.Ṯ
PE/Ṯ = kB.Y
in which kB.Y is a constant, and therefore; PE/Ṯ is the same constant.
The above relationships are exact; there are no tolerances or approximations.

Because we can predict the SHC of elemental matter using the KE (as described above) of only two electrons per orbital shell (State of |Matter; Fig 6) ...
And because PE can only be attributed to an electron in a circular orbit, and PEₙ = mₑ.c² ...
And because 'PEₙ = mₑ.c²' represents the limiting orbital radius of the electron (Rₙ), below which the attraction force exceeds electron's centrifugal force, causing the proton-electron pair to unite ...
We must conclude that Newton and Coulomb were correct; the atom must comprise a nucleus of protons surrounded by their electron partners in circular orbits, two per shell. And this makes perfect sense, because of their same electrical charge polarity, orbiting electrons will naturally position themselves such that they are shielded by the positively charged nucleus.

Additional Verification References

The Electric Atom, PVRT, The States of Matter & The Battery

Further Reading

You will find further reading on this subject in reference publications^{(69, 70, 71 & 73)}