The Electrical Atom
{Keith Dixon-Roche © 07/08/23}Introduction
This work was initiated due to the discovery that the Newton-Coulomb atom predicts the relationship between electrical resistance and temperature.
The purpose of this study is to answer the following questions:
1) Can the Newton-Coulomb atomic model be used to predict the electrical resistivity of elemental matter using mathematics?
2) Can the Newton-Coulomb atomic model be used to predict the properties of an electrical conductor using mathematics?
Note: The essential constants and mathematical symbols are provided at the bottom of this page.
Conclusion
The answer to both the above questions is yes!
Not only is it now possible to describe the mechanical (or magnetic) characteristics of elemental matter using the mathematics of the Newton-Coulomb atom, but it is also possible to describe its electrical properties mathematically using the same model ...
... providing yet more evidence that the Newton-Coulomb version is the correct atomic model.
However, the temperature effect of structural changes to elemental matter, which alters temperature coefficients from linear to non-linear, may make mathematical predictions (using any atomic model) a little more challenging.
Electrical vs Magnetic
Due to the coupling ratio, the electrical (not the magnetic) charges unite all proton-electron pairs.
The electrical particle charges - positive (protons) and negative (electrons) - repel and attract to maintain balance within atoms. Contrary to popular belief, proton-neutron partners do not sit together in atomic nuclei, but are forced apart and oriented (within the atom's innermost shell) in a structural pattern that ensures all proton charges are neutralised (protected) by their neutrons (Fig 1). This pattern is called a lattice structure, and is replicated in atomic collections as elemental matter in both gaseous and viscous conditions; it is responsible for Dalton's law.
The magnetic field generated by each proton-electron pair holds adjacent atoms together as viscous matter, and the electrical charges held by the proton partners push them apart. The magnetic field is therefore responsible for the density of elemental matter and the respective inter-atomic forces (Fₑ & Fₘ) define their viscous-gas condition; transition occurs when the repulsive electrical charge and attractive magnetic field forces are equal; Ṯg: Fₑ = Fₘ.
The density of an atom is that of all the proton-electron pairs - and their neutron partners - within its outermost shell.
The measured gas transition temperature - that of the proton-electron pairs in shell-1 - of elemental matter is that above which, the magnetic field forces are no longer able to resist the inter-atomic [proton] electrical repulsion forces.
Operational electrical current (electron flow-rate) through elemental matter (conductor) occurs when the electrons in its atom's outermost shells are pulled from their orbits.
Temperature
The temperature (Ṯ) of the proton-electron pair in a given shell number (N) is calculated thus: ṮN = Ṯ₁/N
where Ṯ₁ is the measured temperature of elemental matter.
For example; the temperature of the outermost proton-electron pairs (Ṯ₃₇) of a tungsten atom at a measured temperature (Ṯ₁) of 300K;
Ṯ₃₇ = 300/37 = 8.108108108 {K}.
As a proton-electron pair's temperature rises, the electron's orbital radius reduces, increasing its potential energy; making it much harder to pull the electron from its orbit. I.e. electrical resistance and atomic strength both increase with rising temperature.
Voltage (V)
Voltage is measured in Joules per Coulomb, which means the potential energy in an atomic proton-electron pair.
The potential energy in a proton-electron pair is defined by its temperature (Ṯ), and calculated thus: PE = Ṯ.kB' {J}.
The electrical charge in an electron is the elementary charge unit (e) {C}.
Therefore, the Voltage in a proton-electron pair is calculated thus: V = PE/e {J/C}.
For example; the potential energy in the outermost proton-electron pairs of a tungsten atom at a temperature of 300K is;
PE₃₇ = 8.108108108 x 1.31347656477524E-22 = -1.064980998E-21 {J}
and the voltage in this proton-electron pair is;
V₃₇ = -1.064980998E-21 ÷ 1.60217648753E-19 = -6.64708917082E-03 {J/C}
The voltage you need to apply to an atom in order to generate electron flow is that required to pull the outermost electrons from their shells. So, the minimum voltage you need to apply in order to generate a current in tungsten at 300K is 0.0066471 Joules per electron.
Current (I)
DC Current is measured in Coulombs per second, which means the electron flow rate in an atomic proton-electron pair.
The electron flow rate within a proton-electron pair is the speed at which the electron orbits its proton partner, which can be calculated thus;
orbital frequency: ƒ = (Ṯ/Ṯₙ)¹˙⁵/tₙ {/s}
electron flow rate: I = e.ƒ {C/s}
For example; the electron flow-rate in the outermost proton-electron pair of a tungsten atom at a temperature of 300K is;
orbital frequency; ƒ₃₇ = (8.108108108 ÷ 623316124.717178)¹˙⁵ ÷ 5.90596121302193E-23 = 2.5120377566E+10 {/s}
and the current in this proton-electron pair is;
I₃₇ = 1.60217648753E-19 x 2.5120377566E+10 = 4.02472782941E-09 {C/s}
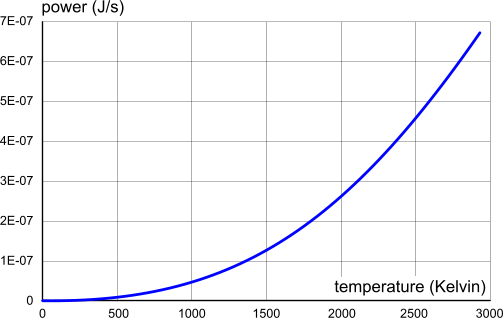
Fig 2. Electrical Power vs. Temperature (proton-electron pair)
Power (P)
Electrical power is the rate at which potential energy is consumed or expended, e.g. Joules per second;
P = V.I = PE/e . e.ƒ = PE.ƒ {J/s}
For example; the power in the outermost proton-electron pair of a tungsten atom at a temperature of 300K is;
P₃₇ = -1.064980998E-21 x 2.5120377566E+10 = -2.6752724770E-11 {J/s}
Resistance (Ω)
Electrical resistance is the resistance in the proton-electron pair to the release of its electron; it is measured in Joules.seconds per Coulomb squared, and may be calculated thus:
Ω = V/I = PE/e / e.ƒ = qₜ.Y.Ṯ/I {J.s / C²}
You will notice that the electrical resistance in a proton-electron pair is based upon Isaac Newton's constant of motion (h = Rₙ.c) for the orbiting electron in its neutronic condition#.
# note: orbital period (t/t) appears and cancels out in the calculation, so the units are correct: kg.m²/s . s/s / C²
For example; the electrical resistance in the outermost proton-electron pair of a tungsten atom at a temperature of 300K is;
Ω₃₇ = -1.064980998E-21 ÷ (2.5120377566E+10 x 1.60217648753E-19²) = -1.6515624044E+06 {J.s/C²}
Electrical resistivity is a moment of resistance, and is measured in 'resistance.metres', and its units of measurement are J.s.m/C².
In an electrical conductor, it is calculated like this: ρ = Ω . A/ℓ
Atomic resistivity: ρₐ = Ω . π.d²/R
The best-fit formula for the inter-atomic [elemental] resistivity is currently; ρₑ = ρₐ . (ψ-1)/Γ
where:
d = atomic spacing (³√[mₐ/ρₘ])
R = orbital radius of the atom's outermost electron shell (Xᴿ/Ṯ₃₇ for a tungsten atom)
ψ = neutronic ratio (1.484459 for a tungsten atom)
Γ = nobility factor; 9.(ψ-1) (4.360135 for tungsten)
(ψ-1)/Γ = 1/9
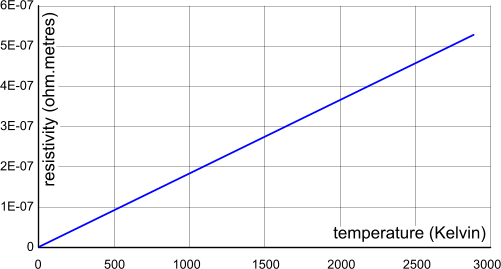
Fig 3. Resistivity vs. Temperature (elemental atom)
Using this calculation procedure, the resistivity (ρₑ) of a tungsten element (Z=74) @ 273.15K is 1.607E-07 J.s.m/C², compared with the average documented value (≈5.3725E-08), and 5.223E-07 @ ≈2884K; i.e. within 20% of the experimental value (≈6.6E-07).
Note: It is important to understand that electrical resistivity varies according to a linear temperature coefficient of resistance. However, if the atomic structure of your elemental matter changes at high temperatures, this variation may no longer be linear, making the mathematical prediction of electrical resistance in viscous matter at very high-temperatures potentially unreliable.
The Electrical Atom
Below is listed a summary of the formulas for the electrical atom:
| Description | Symbol | formula | units |
|---|---|---|---|
| orbital frequency | ƒ | (Ṯ/Ṯₙ)¹˙⁵/tₙ | /s |
| orbital radius | R | Xᴿ/Ṯ | m |
| potential energy | PE | Ṯ.kB' | J |
| electron flow rate | I | e.ƒ | C/s |
| electron retention | V | PE/e | J/C |
| electron resistance | Ω | V/I | J.s/C² |
| proton electrical charge | eꞌ | mₚ.RC . √[Ṯ/Ṯₙ] | C |
| Table 2: proton-electron pair performance | |||
| Description | Symbol | formula | units |
|---|---|---|---|
| shell number | N | INT(Z/2.01+1) | |
| minimum atomic shell temperature | ṮN | Ṯ/N | K |
| minimum atomic potential energy | PE | ṮN.kB' | J |
| minimum electron orbital period | t | tₙ.(Ṯₙ/ṮN)¹˙⁵ | s |
| maximum electron orbital radius | R | Xᴿ/ṮN | m |
| minimum electron flow rate | I | e/t | C/s |
| minimum electron retention | V | PE/e | PE/C |
| minimum atomic resistance | Ω | V/I | J.s/C² |
| minimum atomic power | P | PE/t | J/s |
| atomic resistivity | ρₐ | Ω . π.d²/R | J.s.m/C² |
| elemental resistivity | ρₑ | ρₐ . (ψ-1)/Γ | J.s/C² |
| Table 3: proton-electron pair performance of the outermost electron shell (N) | |||
Electrical Properties
The electrical properties of every proton-electron pair, in any atomic shell, at any temperature, can be calculated using a simple constant (τ):
The temperature of a proton-electron pair in any atomic shell may be determined thus:
let N = atomic shell number
and Ṯ = measured temperature of an atom (or element); i.e. that of the temperature of it's innermost shell (Ṯ₁); shell-1
then ṮN = Ṯ/N
formula;
resistance: Ω = (Ṯₙ/ṮN)⁰˙⁵ . PEₙ.tₙ/e² {J.s/C²}
Voltage: V = (ṮN/Ṯₙ)¹ . PEₙ/e {J/C}
current: I = (ṮN/Ṯₙ)¹˙⁵ . e/tₙ {C/s}
power: P = (ṮN/Ṯₙ)²˙⁵ . PEₙ/tₙ {J/s}
factors:
resistance: τᵣ = Ṯₙ⁰˙⁵ . PEₙ.tₙ/e² = 4.70278098678334E+06 {K⁰˙⁵.J.s/C²}
Voltage: τᵥ = 1/Ṯₙ . PEₙ/e = 8.19807664759932E-04 {J / C.K}
current: τᵢ = 1/Ṯₙ¹˙⁵ . e/tₙ = 1.74324015314324E-10 {C / s.K¹˙⁵}
power: τₚ = 1/Ṯₙ²˙⁵ . PEₙ/tₙ = 1.4291216390641E-13 {J / s.K²˙⁵}
simplified calculation:
resistance: Ω = τᵣ/ṮN⁰˙⁵ {J.s/C²}
Voltage: V = τᵥ.ṮN {J/C}
current: I = τᵢ.ṮN¹˙⁵ {C/s}
power: P = τₚ.ṮN²˙⁵ {J/s}
Whilst this calculation method is simplified, its results are exact; no margin of error or approximation of any kind.
Discussion
Refer to our dedicated web page for a detailed explanation of the electrical resistivity of elemental matter.
The following Table provides the properties, including electrical resistivity, of various GEC tungsten filaments (page 12) compared with theoretical values:
| Power (W) | Diameter (m) | Length (m) | A/ℓ (m) | Resistance (J.s/C²) | GEC Resistivity (J.s.m/C²) | Theoretical Resistivity (J.s.m/C²) |
|---|---|---|---|---|---|---|
| 25 | 3.00E-05 | 0.56 | 1.2622E-09 | 576 | 7.2705E-07 | 5.270413E-07 |
| 40 | 3.30E-05 | 0.38 | 2.2508E-09 | 360 | 8.1028E-07 | 5.270413E-07 |
| 60 | 4.60E-05 | 0.53 | 3.1357E-09 | 240 | 7.5256E-07 | 5.270413E-07 |
| 75 | 5.30E-05 | 0.55 | 4.0112E-09 | 192 | 7.7016E-07 | 5.270413E-07 |
| 100 | 6.40E-05 | 0.58 | 5.5465E-09 | 144 | 7.987E-07 | 5.270413E-07 |
| 200 | 1.02E-04 | 0.72 | 1.1349E-08 | 72 | 8.1713E-07 | 5.270413E-07 |
| Table 4: GE Filament Resistivity based upon filament dimensions vs. atomic performance 120 Volts and operating temperature (≈2884K) Calculation Method: dimensional: ρ = V²/P . A/ℓ; atomic: Ω . π.d²/R . √[ṮN/Ṯg] | ||||||
It should be noted that the theoretical value is based upon a linear temperature coefficient of resistivity, whereas GEC's values, the mean of which is 7.7931E-07, are based upon the filament's physical dimensions and specified power rating.
NBS (National Bureau of Standards) documented value for the resistivity of tungsten at 2873K is expected to be 8.7E-07 J.s.m/C², but the linear interpretation should be ≈6.6E-07 J.s.m/C². It is considered therefore, that these discrepancies in the tested and specified values are due to the alloyed nature of the respective materials.
In other words, when compared with the expected resistivity value 6.6E-07 J.s.m/C²;
GEC's dimensional value is 18.08% greater,
theoretical value is 20.15% lower,
NBS value is 31.82% greater.
In reality, if GEC's filaments are tungsten alloys, which is the norm, their resistivities should be considerably greater than the theoretical values, which is indeed the case.
NBS's tested values for tungsten reveal a non-linear variation in resistivity with temperature which appears to indicate that the structure of elemental matter varies with temperature. And because resistivity variation is due to dimensional distance between adjacent atoms, it is highly likely that tungsten's actual temperature coefficient of expansion is also non-linear.
However, whilst the mathematical prediction of electrical (and dimensional) variation with temperature is possible, and in fact simple, it is considerably more difficult to include the non-linear effects of structural changes to the elemental matter.
Table 1 shows the calculated (theoretical) resistivity values for all the elements (0 to 92) based upon the above formula. You will have noticed that there is a difference between most of them and the documented (experimental) values. However, given the issues with experimentation in terms of materials, environment and equipment, along with the unreliability of many documented values, these differences are understandable.
Essential Constants & Mathematical Symbols
Essential Constants
The primary and principal constants you need to calculate the electrical properties in elemental matter are listed below:
ξₘ = 1836.15115053207
e = 1.60217648753E-19 {C}
tₙ = 5.90596121302193E-23 {s}
Ṯₙ = 623316124.717178 {K}
c = 299792459 {m/s}
PEₙ = 8.18711122262534E-14 {J}
kB = 1.38065156E-23 {J/K}
kB' = 1.31347656477524E-22 {J/K}
X = 6.9353271647894E-09 {K.s²/m²}
Xᴿ = 1.75646616508035E-06 {K.m}
Mathematical Constants
t = electron orbital period {s}
ƒ = electron orbital frequency (1/t) {/s}
g = potential acceleration (proton-electron pair) {m/s²}
m = mass {kg}
N = shell number
PE = potential energy (proton-electron pair) {J}
R = electron orbital radius {m}
Ω = electrical resistance {J.s/C²}
Ṯ = temperature {K}
v = electron orbital velocity {m/s}
ρ = resistivity {J.s.m/C²}
ψ = RAM/Z (neutronic ratio)
ℓ = conductor length {m}
Ø = conductor diameter {m}
A = cross-sectional area of the electrical conductor {m²}
Subscripts
Subscripts:
ₐ atomic
ₑ electrical
ₘ magnetic
N means shell number
ₛ shell number
₁ shell number 1 (innermost shell)
Further Reading
You will find further reading on this subject in reference publications(69, 70, 71 & 73)