The Proton-Electron Pair
{Keith Dixon-Roche © 17/04/18}A description of the proton-electron partnership.
Sources: Planck's Atom; Newton's Atom; Laws of Motion; Physical Constants
Related Books: Philosophiæ Naturalis Principia Mathematica Rev. IV; The Atom; The Mathematical Laws of Natural Science
Related Calculators: Atomic Elements; Orbital Motion; Atoms; Physics
CalQlata comment: This is the only study we (at CalQlata) know on this subject that manifestly works.
Introduction
The purpose of this study is to explain the behaviour of the proton and the electron, as they exist in partnership and within the atom.
The questions are;
1) Does this partnership obey Newton's laws of orbital motion and Coulomb's force law?
2) Does this partnership remain intact inside an atom?
Conclusion
The answer to both of the above questions is yes.
The dimensional and performance properties of a proton-electron pair - both electrical and magnetic - can be predicted using Newton's and Coulomb's force laws, and Newton's & Kepler's laws of orbital motion.
As with all satellite/force-centre partnerships, a proton and electron partnership always obeys the laws of orbital motion even when fused within an atomic structure.
However, in the case of a proton-electron pair, every proton will have only one electron partner, even within an atom.
The Model
The proton-electron pair is a single proton with a single orbiting electron. This is the hydrogen atom.
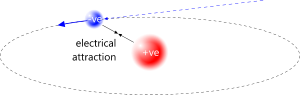
Fig 1. Electron Trapping
There are more protons in the universe than there are electrons.
Protons are positively charged and electrons are negatively charged.
This means that a free-flying electron will be attracted to any lone proton as soon as it comes within range. Once a partnership is established, the proton will collect no more electrons.
Because an electron possesses intrinsic kinetic energy (it must move) it will not attach itself to the proton, it will go into orbit about it. And because the electron is providing its own kinetic energy, its orbit must be circular. And in circular orbits, it is a fundamental law of orbital motion that the potential energy between a satellite (electron) and its force-centre (proton) is always exactly twice the satellite's kinetic energy; PE = -mₑ.v².
And when the electron achieves the speed of light - as in the core of an active star - the pair will unite to become a neutron; PE = -mₑ.c².
How they work
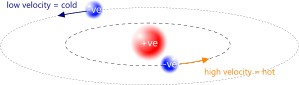
Fig 2. Orbital Radius Varies With Temperature
Electrons and protons exist as proton-electron pairs (H) both within atoms and alone. Their opposite electrical charges provide their mutual attraction. A lone proton (H⁺) will always trap a free-flying electron that is within range (Fig 1). The electron's perpetual motion keeps it in orbit about its proton partner.
An orbiting electron collects energy and charge from its surrounding electro-magnetic energy (EME). It converts the EME to kinetic energy and passes the additional charge on to its proton partner, reducing its orbital radius whilst increasing its velocity; exactly as Newton and Coulomb predicted (Fig 2).
The proton-electron pair continually radiates the EME it collects from its surroundings. If the energy in the surrounding EME is less than the energy of the pair, the electron will slow down and the proton will lose its charge until the electron KE and the surrounding EME balance.
The orbital nature of the opposite electrical charges generates electrical and magnetic fields (Fig 3)
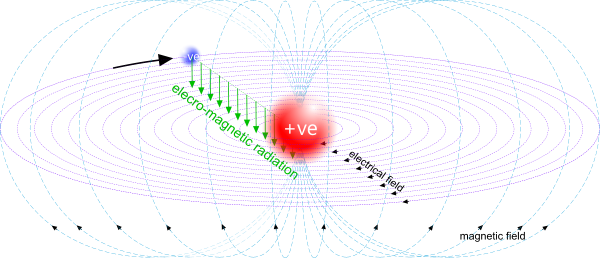
The proton's electrical charge and the pair's electrical field both vary proportionally with temperature.
Irrespective of their environmental temperature, proton-electron pairs (hydrogen atoms) can never become viscous#. That is how we know that it exists as a gas even in the coldest reaches of our universe.
# This is not the case for deuterium or tritium, both of which can exist in viscous form.
Free Electrons
An electron ejected from a proton-electron pair will hold its linear (v) and angular (ω) velocities (at the time of ejection) in free flight until affected by impact or gravity. What we see in bubble chambers as post-impact spiral paths is simply the result of impacting electrons that can be visualised as spinning billiard balls obeying Newton's laws of motion.
Angular velocity in an electron is: ω = 2π / t (t = orbital period at the time of ejection)
Linear velocity of an electron is: v = √[2.KE / mₑ] (at the time of ejection)
Electrons collect and release energy only when in partnership with a proton; i.e. in orbit about the proton.
The higher the electron energy (greater its heat), the greater the electrical attraction between the electron and its proton force-centre (the smaller its orbital radius). This is why electrical resistance in DC circuits rises with increasing temperature.
The greater the proton-electron attraction, the harder it is to pull it from its proton-electron partnership into free-flight.
The greatest speed an orbiting electron can achieve is light-speed, at which it will unite with its proton partner creating a neutron.
This is why it is impossible for an electron to travel in free-flight at light-speed and one of the principal reasons why photons cannot exist.
Properties
The following Table lists the formulas that may be used to calculate the properties of the proton-electron pair. The example shown predicts those properties for a temperature of 300K.
| Property | Formula | Result | Units |
|---|---|---|---|
| Orbital radius | R = XR/Ṯ | 5.85488721693451E-09 | m |
| Orbital velocity | v = √[Ṯ/X] | 207982.67075397 | m/s |
| Orbital period | t = 2πR / v | 1.76876954235065E-13 | s |
| Potential acceleration | g = v²/R | 7.38815108322488E+18 | m/s² |
| Newton's constant of proportionality | K = t²/R³ | 0.15587874533403 | s²/m³ |
| Kinetic energy | KE = ½.mₑ.v² | 1.97021484716286E-20 | J |
| Potential energy | PE = -2.KE = -mₑ.v² | -3.94042969432572E-20 | J |
| Attractive force | F = PE/R = μ.I² | -6.73015473795726E-12 | N |
| Newton's constant of motion | h = R.√[-PE/mₑ] | 1.21771508034132E-03 | m²/s |
| Electro-magnetic frequency | ƒ = 1/t | 5.65364778201136E+12 | Hz |
| Electro-magnetic wavelength | λ = c/ƒ | 5.30263770505606E-05 | m |
| Electro-magnetic amplitude | A = R | 5.85488721693451E-09 | m |
| Proton electrical charge | e' = mₚ.RC . √[Ṯ/Ṯₙ] | 2.04091646600168E-19 | C |
| Voltage | V = -PE/e | 0.24594229942798 | V or J/C |
| Current | I = e.2πƒ = e.g/v | 5.69139818666179E-06 | A or C/s |
| Resistance | R = V/I | 43212.9841142311 | Ω or J.s/C² |
| Magnetic field | μ = mₑ.R/e² | 0.207772041572393 | kg.m/C² |
| The Properties of a Proton-Electron Pair @ 300K these calculations correctly predict the properties of a proton-electron pair at any temperature |
|||
Calculation Results
The following Table lists the calculation results for the performance and properties of a proton-electron pair - together with a comparison between Newton's and Coulomb's forces and energies - at various temperatures:
| Ṯ (K): | 6 | 210.193329 | 361962.555 | 623316125 | units |
|---|---|---|---|---|---|
| t | 6.25354469E-11 | 3.01595420E-13 | 4.22043938E-18 | 5.90596121E-23 | s |
| Orbital Shape: | |||||
| R | 2.92744361E-07 | 8.35643156E-09 | 4.85261843E-12 | 2.81793795E-15 | m |
| e | 0 | 0 | 0 | 0 | |
| A | 2.69232168E-13 | 2.19377253E-16 | 7.39779274E-23 | 2.49466782E-29 | m² |
| L | 1.83936707E-06 | 5.25050080E-08 | 3.04899008E-11 | 1.77056263E-14 | m |
| K | 1.55878745E-01 | 1.55878745E-01 | 1.55878745E-01 | 1.55878745E-01 | s²/m³ |
| Electrical Performance (Coulomb): | |||||
| v | 2.94131914E+04 | 1.74090867E+05 | 7.22434281E+06 | 2.99792459E+08 | m/s |
| ac | 2.95526043E+15 | 3.62686269E+18 | 1.07552509E+25 | 3.18940729E+31 | m/s² |
| F | 2.69206190E-15 | 3.30385056E-12 | 9.79737722E-06 | 2.90535539E+01 | N |
| Fc | 2.69206190E-15 | 3.30385056E-12 | 9.79737722E-06 | 2.90535539E+01 | N |
| PE | -7.88085939E-22 | -2.76084011E-20 | -4.75429333E-17 | -8.18711122E-14 | J |
| KE | 3.94042969E-22 | 1.38042006E-20 | 2.37714666E-17 | 4.09355561E-14 | J |
| E | -3.94042969E-22 | -1.38042006E-20 | -2.37714666E-17 | -4.09355561E-14 | J |
| h | 8.61054591E-03 | 1.45477841E-03 | 3.50569791E-05 | 8.44796548E-07 | m²/s |
| PE/KE | -2.0000000000 | -2.0000000000 | -2.0000000000 | -2.0000000000 | |
| ω | 1.00473981E+11 | 2.08331589E+13 | 1.48875147E+18 | 1.06387175E+23 | ᶜ/s |
| Mechanical Performance (Newton): | |||||
| mₚ | 1.67262164E-27 | 1.67262164E-27 | 1.67262164E-27 | 1.67262164E-27 | kg |
| mₑ | 9.10938970E-31 | 9.10938970E-31 | 9.10938970E-31 | 9.10938970E-31 | kg |
| v | 6.17496390E-16 | 3.65483909E-15 | 1.51666834E-13 | 6.29380059E-12 | m/s |
| ac | 1.30250772E-24 | 1.59851112E-21 | 4.74029201E-15 | 1.40570610E-08 | m/s² |
| F | 1.18650504E-54 | 1.45614607E-51 | 4.31811673E-45 | 1.28051247E-38 | N |
| Fc | 1.18650504E-54 | 1.45614607E-51 | 4.31811673E-45 | 1.28051247E-38 | N |
| PE | -3.47342661E-61 | -1.21681850E-59 | -2.09541728E-56 | -3.60840469E-53 | J |
| KE | 1.73671330E-61 | 6.08409250E-60 | 1.04770864E-56 | 1.80420234E-53 | J |
| E | -1.73671330E-61 | -6.08409250E-60 | -1.04770864E-56 | -1.80420234E-53 | J |
| h | 1.80768586E-22 | 3.05414127E-23 | 7.35981272E-25 | 1.77355395E-26 | m²/s |
| PE/KE | -2.0000000000 | -2.0000000000 | -2.0000000000 | -2.0000000000 | |
| ω | 2.33374242E+13 | 2.86410064E+16 | 8.49332433E+22 | 2.51864607E+29 | ᶜ/s |
| Coupling Ratio: | |||||
| √φ | 2.09938589E-20 | 2.09938589E-20 | 2.09938589E-20 | 2.09938589E-20 | v/v## |
| φ | 4.40742112E-40 | 4.40742112E-40 | 4.40742112E-40 | 4.40742112E-40 | a/a# |
| φ | 4.40742112E-40 | 4.40742112E-40 | 4.40742112E-40 | 4.40742112E-40 | F/F# |
| φ | 4.40742112E-40 | 4.40742112E-40 | 4.40742112E-40 | 4.40742112E-40 | Fc/Fc# |
| φ | 4.40742112E-40 | 4.40742112E-40 | 4.40742112E-40 | 4.40742112E-40 | PE/PE# |
| φ | 4.40742112E-40 | 4.40742112E-40 | 4.40742112E-40 | 4.40742112E-40 | KE/KE# |
| φ | 4.40742112E-40 | 4.40742112E-40 | 4.40742112E-40 | 4.40742112E-40 | E/E# |
| √φ | 2.09938589E-20 | 2.09938589E-20 | 2.09938589E-20 | 2.09938589E-20 | h/h## |
| Proton-Electron Pair Performance Neutronic Radius speed of light # magnetic:electrical ratios: /s² ## magnetic:electrical ratios: /s |
|||||
As soon as the electron's velocity (v) reaches the speed of light (c), the magnetic field force generated by the pair will exceed the electron's centrifugal force, and the pair will unite (see The Neutron; Fig 1).
Whilst the above description and formulas are sufficient to analyse any atom at any temperature, the publications referenced below (Further Reading) provide considerably more detail to that shown above.
Whilst this model is today ignored, and in fact denied, by all the world's physicists, be in no doubt; it does indeed describe the basic principles of the atom. And is the single most important discovery in physics in the last 150-years. It has also been verified; see the Atom.
We have even provided online and downloadable calculators that predict the properties of any atom at any temperature simply from its atomic number to support this fact.
The electricity generated in a proton-electron pair at the instant of the creation of a neutron is provided in the The Electrical Atom
Further Reading
You will find further reading on this subject in reference publications(69, 70, 71 & 73)