The Neutron

{Keith Dixon-Roche © 01/10/18}

An explanation of the neutron.

Sources: The Proton-Electron Pair; The True Atom; Laws of Motion; Physical Constants
Related Books: Philosophiæ Naturalis Principia Mathematica Rev. IV; The Atom; The Mathematical Laws of Natural Science
Related Calculators: Orbital Motion; Atoms; Physics
CalQlata comment: This may well be Keith Dixon-Roche's most important discovery, and should mean the final solution to all our energy problems.

Introduction

The purpose of this study is to define the origins and properties of the neutron:
The question is;
1) What is a neutron?
2) What is its purpose?

Conclusion

The neutron is the source of all universal energy, including the 'Big-Bang'.
They are created in stars as a result of high-temperature, and can only exist within an atom.
Each neutron holds 1.63785606465701E-13 Joules of energy.
The natural reversion of neutrons into their component parts (electron and proton) is the cause of atomic half-life.

The Model

The neutronic model is simple; it is a proton-electron pair that has united due to high temperature.

Unity Forces

The forces uniting a proton-electron pair

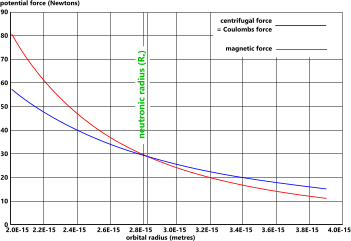
Fig 1. Creation of a Neutron

The centrifugal force in an orbiting electron (Fc) follows Newton’s laws of orbital motion.
The potential force generated by the magnetic field (Fm), however, varies with orbital radius as shown in Fig 1.

At orbital radii greater than the neutronic radius (Rₙ), the balancing potential forces of an orbiting electron are as follows:
FG = FE = Fc > Fm

At the neutronic radius (Rₙ), the balancing potential forces of an orbiting electron are as follows:
FG = FE = Fc = Fm

At orbital radii less than the neutronic radius (Rₙ), the balancing potential forces of an orbiting electron are as follows:
FG = FE = Fc < Fm

Where the forces are calculated as follows:
Potential: FG = -G.mₑ.mₚ / φ.R² {m³ / kg.s² . kg² / m² = kg.m/s² = N}
Electrical: FE = -k.e² / R² {kg.m³ / C².s² . C²/m² = kg.m/s² = N}
Centrifugal: Fc = mₑ.v² / R {kg.m²/s² / m = kg.m/s² = N}
Magnetic: Fm = μ.g.e² / R {kg.m/C² . m/s² . C²/m = kg.m/s² = N}
    = mₑ.c².Rₙ² / R³ {kg.m²/s² . m²/m³ = kg.m/s² = N}
    and:
    g = -G.mₚ / R².φ {m³ / kg.s² . kg / m² = m/s²}
    μ = Rₙ.mₑ/e² = 1E-07 {kg.m / C²}
    R is electron orbital radius
    v is electron orbital velocity

When the magnetic field force (Fm) between the proton and the electron exceeds the electron's centrifugal force (Fc), the pair will unite and become a neutron, which occurs when the electron achieves light-speed, which occurs at the neutronic temperature, at which time the electron will be orbiting at the neutronic radius (Fig 1).

Neutron Energy

When a proton-electron pair achieves the neutronic temperature, the two particles unite to create a neutron, storing the energy they were generating at the time of their union.
This energy is released when the neutronic ratio of an element exceeds 1.6
This is the process generating additional heat within stars; neutron creation and fissionable energy release.

The energy held by a neutron can be calculated as follows:
Eₙ = |KE| + |PE| + |SE|

Kinetic Energy: KE = ½.mₑ.c²
= ½ x 9.1093897E-31 x 299792459
= 4.09355561131267E-14 J

Potential Energy: PE = -mₑ.c²
= -9.1093897E-31 x 299792459
= -8.18711122262534E-14 J

Proton Spin Energy: SEₚ = E₃ = KEₑ+PE
    = 4.09355561131267E-14 J + -8.18711122262534E-14 J
    = -4.09355561131267E-14 J
Electron Spin Energy: SEₑ = E₀ – E₁ – E₃
Jₑ = ⅖.mₑ.rₑ² = 7.66586456056651E-63 kg.m²
ωₑ = 2π/tₙ = 1.06387175271756E+23 ᶜ/s
E₀ = ½.Jₑ.ωₑ² = 4.33820131944073E-17 J
E₁ = δKE.(rₑ/Rₙ)² = 0 J {δKE = 0}
E₂ = 0 J
SEₑ = 4.33820131944073E-17 J
Spin Energy: SE = SEₚ + SEₑ
SE = |-4.09355561131267E-14 + 4.33820131944073E-17|
    = 4.09789381263211E-14 J

Eₙ = |KE| + |PE| + |SE| = 1.63785606465701E-13 J
The total energy in a proton-electron pair at 300K is; E = 7.88085938865144E-20 J

Note: After removing its protective neutron, an adjacent proton will be ejected according to Coulomb's force law, releasing the following kinetic energy:
KEₚ = k.e²/C = 1.3954267683677E-14 J
where; proton separation: C = 4.Rₙ²/(Rₚ+Rₑ) = 1.65331294837664E-14 m

The electricity generated in a proton-electron pair at the instant of the creation of a neutron is provided in the The Electrical Atom

Verification:

Apparently, when 'Little Boy' was dropped on Hiroshima ...
... ≈1.0kg of its mass was destroyed releasing 6.3E+13 Joules of energy (empirical value).

U₂₃₅ has a neutronic ratio of: ψ = 1.587270761
1 kg of which contains:
3.66585231725022E+26 neutrons (Nₙ) and 2.30953181248165E+26 protons (Nₚ)
According to the Newtonian atom, 'Little-Boy' released:
E = Nₙ.Eₙ + Nₚ.KEₚ = 6.3264167012986E+13 Joules of energy

Orbital Support Calculations

RAC = kB.Rᵢ.Qₑ = 96485.3317942156 C/mol (of electrons)
Note: Faraday's constant = 96485.3317942158 C/mol {exact}

Rest condition @ Ṯ = 1K:
Nt = 1 Nᵥ = 1.5 Np = 2.5

RAMp = Rᵢ.mp/kB = 1.00727638277235 g/mol
Note: RAMH = 1.00794 g/mol (hydrogen)
RAMₑ = Rᵢ.mₑ/kB = RAMp . mₑ/mp = 0.000548580318390698 g/mol
Rₐ = RAMₑ / Rᵢ = 15156.3563034308 J/g/K
R = Rₐ.mp = 1.38065156E-23 J/K
kB = 1.38065156E-23 J/K
kB.NA.Ln(Nt) = cp.Ln(Ṯ).RAMₑ = 3.371231032 J/K/mol
exp(2.5xLn(Ṯ)) = 1

cᵥ = Nt.Rₐ = 22734.5344551462 J/g/K
Cᵥ = mₑ.cᵥ = 2.07097734E-23 J/K
cp = cᵥ+Rₐ = 37890.8907585769 J/g/K
Cp = mp.cᵥ = 3.4516289E-23 J/K

KEₑ = kB.Ṯ.Nₚ = 3.4516289E-23 J

X = mₑ² / mₚ.kB = 3.5933271974345800E-11 K.s² / m²
Ṯ = X.v² K
Note: Ṯ = X.v²/e²; but because e is a constant, the formula has been reduce to that shown above

According to Newton's orbital motion formula; v = √[R.g]
when electron velocity 'v' reaches the speed of light (c):
Rn = orbital radius of 1.46677550700177 x (Rn + rₑ) = 2.817937953839E-15 m
Electrostatic acceleration: gₑ = G.mp / φ.Rn² = 3.18940728807829E+31 m/s²
Ṯ = 623316124.717178 K

The iron atom (2.8E-10m) was measured at ≈-66.44°C

The magnetic field 'B' as described by Lorentz, is actually 1/RC, which is relative charge capacity (1.75881869180547E+11 C/kg). And the orbital radius at which an electron and a proton combine to create a neutron may be calculated as follows:

Rn = μ.e.RC = 2.817937953839E-15 m According to the 'heat-to-electron-velocity' formula this orbital radius occurs when the electron is travelling at the speed of light.

Below the orbital radius; 'Rn', the attractive magnetic charge exceeds the repulsive electrical charge and the electron combines with its proton to create a neutron, which occurs when the electro-magnetic energy is equivalent to a temperature of 623316124.717178K

Moreover, 'Rn' occurs when: KE = ½.m.c²
Note: In circular orbits; PE = -2.KE = -2 . ½.m.c² = -m.c²

The magnetic constant (μₒ), which controls this union between an electron and a proton, is referred to as;
μₒ = 1E-07 . 4π H/m,
but what exactly is 1E-07 and what is a Henry?
mₑ.Rn/e² = 1E-07 (exactly) kg.m/C²
μₒ = 4.π.Rn.mₑ/e² kg.m/C²
and;
Henry = kg.m²/C²

Verifying that 'Rn' is a real and important physical constant (that I refer to as the neutronic radius) and that it occurs when PE = m.c²

This is the rationale behind E = m.c²

Moreover, all of the above can only be determined using Newtons laws of motion and Coulomb's electrical force. None of this is achievable with Relativity, in which mass is claimed to vary with velocity, and gravity (non-polar magnetism) is claimed to deform the orbital path.

In close proximity to other neutrons and the electro-magnetic field generated by other proton-electron pairs within the nucleus of an atom, neutrons will gradually split into their component parts; an electron and a proton. The rate at which this occurs is dependent upon the size and structure of the nucleus.

A neutron therefore has no electrical charge but possesses a magnetic charge and its mass is that of a proton plus that of an electron.

It cannot be mere coincidence that Newton's and Coulomb's laws show that an electron orbiting its proton at the speed of light (c) comes within striking distance of each other, that Newton's and Coulomb's laws can explain all of the above clearly and accurately, but Relativity cannot.