Planetary Spin Theory
{Keith Dixon-Roche © 14/03/17}A mathematical explanation for the cause of spin in all the celestial bodies in our solar system; its sun, planets, moons and comets.
It also explains the relative spin directions of Venus and Mercury, along with the source of the internal [frictional] heat in stars and planets, and the nature of gas planets.
Sources: Solar System Orbits; Laws of Motion; Physical Constants; Newton's 'G'
Related Books: Philosophiæ Naturalis Principia Mathematica Rev. IV; The Theory of Spin; The Mathematical Laws of Natural Science
Related Calculators: Orbital Motion; Physics; Planetary Spin
Online Calculator: Planetary Spin
CalQlata comment: This is the only study we (at CalQlata) know on this subject that manifestly works.
(Refer to Mathematical Symbols & Units for an explanation of the terminology, mathematical symbols and units in this web page)
Introduction
The purpose of this study is to answer the following questions:
1) What causes a star or a planet to rotate on its axis?
2) What defines the magnitude and direction of this rotation?
Conclusions
Isaac Newton's orbital forces are responsible for inducing spin in all celestial bodies; both external and internal (frictional heat).
Total spin energy (E₂) in any and all celestial bodies comprises three components:
E₀; the spin induced in a satellite by the potential energy between it and its force-centre; anchors a satellite's core.
E₁; the torque induced in a satellite by its force-centre's spin; drives a satellite's matter counter to its force-centre.
E₃; the spin induced in a satellite by its own [sub-]satellites; drives a satellite's matter.
E₂ = E₁-E₀-E₃
The internal heat in all celestial bodies is due to the conflicting rotational forces induced in a satellite by its force-centre and its sub-satellites.
The relative rotation of the atomic charges in a celestial body's core and its mantle elements is responsible for generating its protective magnetic field.
Only satellites that are also force-centres can generate internal friction; heat and magnetic fields.
The greater a satellite's sub-satellite mass, the more internal heat it will generate and the more intense its magnetic field.
Satellites with no sub-satellites, such as Mercury, Venus and all moons, generate negligible internal friction.
A gas planet is simply a planet that generates sufficient internal frictional heat to melt its crust.
A star is simply a gas planet that has managed to generate sufficient internal heat (through spin-friction) to raise its core matter to the neutronic temperature, and thereby initiate fissionable decay.
The reason Venus spins in the opposite direction to Mercury, is because the sun's rotational component (E₁) is greater in Venus than it is in Mercury and neither planet has sub-satellite(s) to counter this energy.
Planetary spin can be used, together with core pressure, to calculate the internal properties of a planet or star
Further Work
Is Mars hollow?
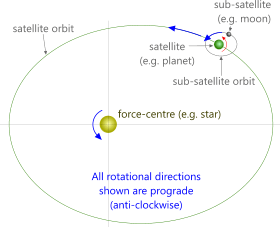
Fig 1. The Basic System
The Basic System
The basic system (Fig 1) comprises;
a force-centre (e.g. a star); and
an orbiting satellite (e.g. a planet); and
a secondary orbiting satellite (e.g. a moon)
Methodology
The following procedure was used to establish the controlling formulas for planetary spin using our solar system for verification:
Isolate and identify the relative angular direction(s) imposed on a planet by its force-centre and its satellite(s) and determine the energy sources responsible for their generation.
It will be assumed that only orbiting bodies and their force-centres can induce spin in each other, which is actually correct as all spin energies can be found from Newtonian mechanics.
Calculations
The polar moment of inertia of any non-homogeneous body may be calculated thus:
J = ⅖.m.(Δ.r)²
Spin energy may be calculated thus:
E = ½.J.ω²
The relative angular velocities induced in a planet (or star) are defined below.
The Orbit
ωₒ: the natural angular velocity of a lone planet (with no moons) orbiting a star rotating at the same angular velocity as its planet.
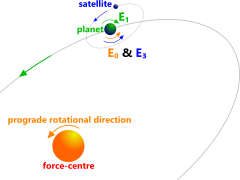
Fig 2. Spin Energie Directions
ωₒ = 2π / tₒ
Eₒ = ½.J.ωₒ²
The gravitational energy between the core of a sun and that of its planet will induce spin (ωₒ) in the planet with the same direction and period as that of its sun
(e.g. Fig 2; +ve or prograde).
If a sun has only one planet with no moons, they would both have the same angular velocity (ω₁ = ωₒ). Otherwise, the sun and planets would spin at different rates.
This is the starting point for the calculation procedure.
The Force-Centre
ω₁ is angular velocity in a satellite generated by its own orbital kinetic energy and varies with the distance between it and its force-centre according to Isaac Newton's inverse-square relationship
E₁ = δKE . (r/R )²
This energy will cause a planet to rotate in the opposite direction (e.g. Fig 1; -ve or retrograde)
The Satellites
ω₃ is the angular velocity induced in a force-centre by its orbiting satellite(s)
E₃ = Σ(KEᴾ + PEᴬ) . Sign[Cos(θ)]
Σ(KEᴾ + PEᴬ) must be negative before θ is applied
Satellites induce spin throughout the mass of their force-centre in the same direction as their orbit.
If the plane of a satellite's orbit is tilted (θ) greater than 90º relative to the plane of the planet's orbit, or if it is orbiting in the opposite direction to the planet's orbit about its force centre, the energy it induces (E₃) must be multiplied by -1 {i.e. Sign[Cos(θ)] }
The Planet's Angular Velocity
The energy inducing the angular velocity of a planet (E₂) may be calculated thus:
E₂ = E₁ - E₃ - Eₒ
Note: E₃ in the above formula is minus because it is a negative value in Newtonian mechanics
The angular velocity of a planet (ω₂) may be calculated thus:
ω₂ = √[2.E₂ / J₂]
This calculation method predicts all reversed spins; e.g. Venus, Uranus and Pluto
Related Mathematical Relationships
1 + ½e² = π.R ² / Aₒ
In which Aₒ is the area of satellite's orbit as calculated in Newton's Laws of Motion
and R is the average distance of a satellite from its force-centre as calculated in Newton's laws of motion
The orbital energy that defines the angular velocity of a force-centre may be calculated thus:
E = m.Aₒ.ω₂ₒ² / 2.π.(1-½e²)
In which E is the total energy calculated in Newton's Laws of Motion
Calculation Results
The following Table shows the relevant spin energies in some of the bodies in our solar system:
| J | Eₒ | E₁ | E₃ | E₂ | ω₂ | |
|---|---|---|---|---|---|---|
| Kg.m² | J | J | J | J | ᶜ/s | |
| Sun | 3.91229E+46 | 1.46587E+16 | 5.01045E+32 | -1.60100E+35 | 1.60602E+35 | 2.86533E-06 |
| Mercury | 5.19308E+35 | 1.77447E+23 | 5.76563E+23 | 0 | 3.99116E+23 | 1.23980E-06 |
| Venus | 3.30863E+37 | 1.73281E+24 | 2.51495E+23 | 0 | -1.48132E+24 | -2.99237E-07 |
| Earth | 1.08212E+37 | 2.14478E+23 | 3.20800E+23 | -2.87708E+28 | 2.87709E+28 | 7.29212E-05 |
| Mars | 1.58326E+31 | 8.87109E+16 | 1.55612E+22 | -2.42128E+22 | 3.97739E+22 | 7.08824E-05 |
| Jupiter | 1.92586E+39 | 2.71288E+23 | 2.52842E+26 | -2.97774E+31 | 2.97777E+31 | 1.75853E-04 |
| Saturn | 1.52389E+38 | 3.48093E+21 | 9.19174E+24 | -2.04404E+30 | 2.04405E+30 | 1.63788E-04 |
| Uranus | 1.38902E+37 | 3.90074E+19 | 2.80792E+22 | 7.11807E+28 | -7.11807E+28 | -1.01238E-04 |
| Neptune | 3.47506E+37 | 2.53648E+19 | 2.09365E+21 | -2.03937E+29 | 2.03937E+29 | 1.08338E-04 |
| Pluto | 5.48500E+35 | 1.76850E+17 | 6.27106E+15 | 3.55515E+25 | -3.55515E+25 | -1.13856E-05 |
| Moon | 2.73159E+34 | 9.67616E+22 | 1.93523E+23 | 0 | 9.67616E+22 | 2.66170E-06 |
| Phobos | 4.04662E+22 | 1.05210E+15 | 2.10421E+15 | 0 | 1.05210E+15 | 2.28033E-04 |
| Deimos | 4.68802E+18 | 7.77805E+09 | 1.55566E+10 | 0 | 7.77854E+09 | 5.76062E-05 |
| Calculated energy values for planetary spin | ||||||
Spin Direction
Planetary spin direction can be determined from the component spin energies; E₀ E₁ E₂ E₃.
A) E₀: The potential energy between a satellite and its force-centre 'centres of mass' acts as a core-anchor.
B) E₁: The rotation induced in a satellite's mass by the spin in its force-centre is dependent upon the radial relationship; 'r:R'. This [satellite] spin direction is counter to the force-centre's spin direction.
C) E₃: The rotation induced in a satellite's mass by its own sub-satellites is by far the most dominant spin energy. This [satellite] spin direction is the same as the sub-satellite orbital direction.
If we select the positive spin direction clock-wise from a plan view, total spin energy; 'E₂' is calculated as described above.
So why do Venus and Uranus spin in the opposite direction?
Both Venus and Mercury have no satellites# so; E₃ is zero. The only energies inducing spin in these planets are E₁ & -E₀.
# Their force-centre's gravitational pull is too dominant to allow these planets to trap galactic comets.
Venus is a large planet, so 'E₁' is greater than 'E₀'; 'E₀' therefore defines the planet's spin direction.
Mercury is a small planet, so 'E₁' is less than 'E₀'; 'E₁' therefore defines the planet's spin direction.
Uranus spins in the opposite direction because its spin axis is greater than 90°
Chicken & Egg?
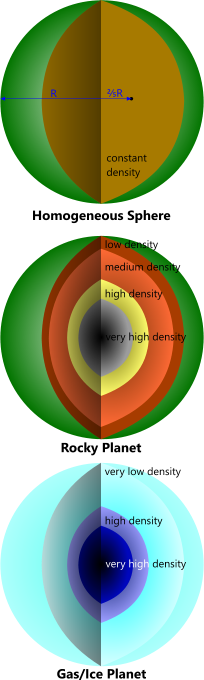
Fig 3. Polar Moment of Inertia
It is currently believed that our solar system was initiated by our sun rotating under its own steam pulling its planets around with it. If so, it would need a suitable energy source causing it to do so; and if it applies to stars, it must allso apply to planets, moons and galactic force-centres. Moreover, whilst this claim may (or may not) be made for our sun and even Earth itself, it cannot explain Pluto's local orbit.
A celestial body can only spin if an external force causes it to do so; conservation of energy. And the gravitational energy between it and its orbital partners (force-centre and satellites) can be the only means of inducing this spin. Therefore, spin in any celestial body can only occur after it has begun oriting a force-centre and/or collecting a satellite. Therefore, spin came last.
Therefore, current beliefs must be wrong; orbits existed before spin.
Polar Moment of Inertia (Δ)
The basic formula for the polar moment of inertia (J) of a sphere is:
J = ⅖.m.r²
Where 'm' is the mass of the sphere and 'r' its radius (Fig 3)
However, this formula only applies to a sphere that comprises the same homogeneous material throughout its structure. Planets, however, are anything but homogeneous as gravitational energy generates very high densities at their cores (Fig 4)
'Δ' in the above formula can provide us with an equivalent representative radius of an homogeneous sphere with the same mass and the correct polar moment of inertia (J) as follows:
Eₒ = ½.J.ωₒ²
J = ⅖.m.(Δ.r)²
The calculated variable; 'Δ' for various solar system bodies is provided in the following Table
| Delta values for solar system bodies | |
|---|---|
| Body | Δ |
| Sun | 0.318782372247959 |
| Mercury | 0.812862196423113 |
| Venus | 0.681180492057101 |
| Earth | 0.33428172721771 |
| Mars | 0.00231707805666362 |
| Jupiter | 0.0227806693989634 |
| Saturn | 0.014059868482105 |
| Uranus | 0.0249372276830553 |
| Neptune | 0.0374067226435373 |
| Pluto | 8.64241935542982 |
| Moon | 0.554903433736135 |
| Phobos | 0.275895222790585 |
| Deimos | 0.014346539805995 |
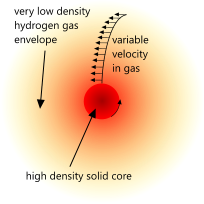
Fig 4. Variable Density
'Δ' Unknown
If you know a satellite's surface rotation rate and orbital properties, you can calculate its Δ value using the following calculation procedure:
E₁ and E₃ can be found from Newton's orbital calculations.
ωₒ is the satellite's orbital rate.
ω₂ is the satellite's spin rate (ω₂ = 2π/tₛ).
The satellite's polar-moment of inertia can be found from:
J = 2.(E₁-E₃) / (ωₒ.|ωₒ| + ω₂.|ω₂|)
Δ = √[5.J / 2.m] / r
E₀ = ½.J.ωₒ.|ωₒ|
E₂ = ½.J.ω₂.|ω₂|
ω₁ = sign(E₁) . √[2.E₁ / J]
ω₃ = sign(E₃) . √[2.E₃ / J]
Used together with Core Pressure, the above value 'Δ' can be used to establish the composition of a planet or star.
Care should be taken when estimating the structure of gas-planets. The above calculation procedure requires an accurate value for the spin rate of surface of the planet itself (ω₂), not the outer surface of its gas cloud, which is all we see through a telescope.
However, it is reasonable to assume that a gas planet comprises similar matter to all other celestial bodies and that their 'Δ' values are slightly less than that of the Earth (< 0.33). Their gas clouds are almost definitely spinning faster than the planet itself.
Internal [Frictional] Heat
All satellites that are also force-centres (host sub-satellites) will generate internal heat through friction.
The spin direction of a satellite is always dominated by the orbital direction of its own substantial sub-satellites (e.g. moon(s)). This sub-satellite kinetic energy (E₃) acts throughout the satellite's mass.
But the potential energy between a satellite and its force-centre (E₀; preventing the satellite's core from rotating), together with the force-centre's induced torque (E₁; core rotation in the opposite direction), will cause the satellite's core to spin (ω₀ + ω₁) relative to its mantle matter (ω₃).
This relative rotation between a satellite's core and its mantle generates internal friction. The amount of energy and the relative rotation rates can be calculated as follows:
Input Data
ρc = core density (expected value; 7870 kg/m³; iron)
rc = core radius
ρm = mantle density
rm = satellite outside radius
Ec = E₀
Δc = 1 (≈ homogeneous)
Output Data
Core:
mc = ρc / Vc
Jc = ⅖.mc.rc²
ωc = √[2.Ec / Jc]
Mantle:
mm = ρm / Vm
Jm = J - Jc
Δm = √[5/2.Jm / mm.(rm² - rc²) ]
Em = E₃ - E₁
ωm = √[2.Em / Jm]
Effective (relative):
δω = ωm - ωc
δE = Em - Ec
For our Earth:
δω = -6953426E-05 ᶜ/s
δE = -2.877061E+28 J (friction and heat)
If the internal [core] heat reaches the neutronic temperature, fissionable energy will be generated, making the body bright in the night sky.
The Planets
From this study, it appears unlikely that the earth, or any other planet spent its first half-billion years or so in a molten or even especially heated condition. Accretion doesn't generate heat and there is no physical evidence on earth to indicate such a condition during its early life. Moreover, the fact that the earth's internal heat is not left over from its birth but constantly generated by the competing spin-related influences from its force-centre and its satellite seems to indicate otherwise.
Together with Core Pressure, spin theory allows us to estimate the internal composition of the satellites in our solar system: e.g. Core Pressure our own planet; Fig 1.
Venus
The reason Venus spins in the opposite direction to the other planets is defined above
Refer to Example Calculation 1 for the mathematical reason.
Venus is, and always has been, too close to the sun to allow water to exist on its surface in liquid form. The mass of water vapour (similar to that on the surface of the earth) maintains the surface temperature of Venus. Almost all its surface heat comes from the sun and is retained by atmospheric water vapour.
Whilst Venus contains a similar percentage of iron to the earth, it has a far lower concentration at its core because it has no moon. The earth's moon is, and always has been, responsible for the differential spin-rate of the earth's core and its mantle and thereby generating its magnetic field and its internal heat, providing the mechanism for its iron to migrate towards its core. Venus has no magnetic field or internal heat because its core is not spinning at a different rate to its mantle.
Because Venus has no rotating core and no liquid surface water, it has no mantle plumes, low volcanic activity and therefore cannot generate active tectonic-plates.
The reason Venus' erupted surface material is so flat (non-effusive) is because, having no mantle plumes and little internal heat, its volcanic activity is much less aggressive than that within the earth.
Mars
Whilst it remains a mystery, the most likely reason for Mars' low density (3934.1 kg/m³) and exceptionally low 'Δ' value, is that ...
... during its early life, Mars probably had a single moon (Deimos) that was sufficient to provide the internal frictional heat required to generate tectonic activity. This activity in its surface crust would have provided an environment suitable for plant life to proliferate and thereby, generate an oxygen-rich atmosphere.
When it trapped Phobos, however, the internal frictional heat became so intense that the planet's mantle core was blasted onto its surface, leaving behind a [relatively] hollow (or porous) mantle, along with the largest dormant volcano on the surface of one of our solar system's smallest planets, and covering up all evidence of its earlier plant-life.
The atmospheric oxygen and surface water at this time will have oxidized the iron-rich mantle matter lying on its surface, giving the planet its distinctive colour.
Eventually, all of the planet's surface water and atmospheric gasses will have been subsumed into the planet. It may be that some frictional heat is still being generated internally, keeping its innermost water liquid.
Mars is by far the most interesting planet in our solar system, because:
if it is a hollow iron planet,
if it has had liquid water on its surface,
if it has been host to oxygen emitting plant-life,
if its water has found its way into the planet's interior,
It is highly likely that the kinetic energy in Phobos will keep the water liquid and potentially relatively warm. This means that:
a) it may contain oxygen internally, and
b) it may contain life internally, and
c) it may be possible to occupy its internal voids
Pluto

Fig 5. Pluto's Local Orbit
Pluto is probably the most active planet in our solar system, having collected sufficient comparative satellite mass to pull the planet into a local orbit (Fig 5), and is the reason why its effective radial modifier (Δ) is greater than 1.
This is the only reason it doesn't generate enormous amounts of internal frictional heat.
Pluto is the only planet in these calculations with a 'Δ' value greater than 1 and the only planet being pulled by its moon into a significant localised orbit, thereby vindicating a value of; 'Δ>1' and the use of this variable in these calculations.
Relative Densities
As we can only guestimate the structures of our sun or the ice and gas planets, we can only guestimate their polar moments of inertia. To do this, we may use the known values for ωₒ and Eₒ to establish a representative radial modifier 'Δ' (see Polar Moment of Inertia (Δ) above). We can then use 'Δ' to estimate the expected surface density for each planet based upon its average density.
For each 'Δ' to be representative, it must reflect the structure of the planet concerned. A reasonable estimate can be made from the average densities of each planet.
By way of illustration, it is possible to estimate for most planets from their relative densities
'ρˢ = Δ.ρᵅ'
Where: ρᵅ is the average density and ρˢ is the surface density
Using this argument for the planets in our solar system with moons, the surface densities of each are estimated as follows:
Given their respective surface temperatures and despite the unknown nature or composition of each planet's inner material(s), with the exception of Mars and Pluto, each is representative of its expected surface materials.
Table 1 shows the relevant properties of the bodies in our solar system:
| Δ | Surface Density (kg/m³) | |
|---|---|---|
| Earth | 0.334281727 | 1840.672632 |
| Mars | 0.002317078 | 9.115572455 |
| Jupiter | 0.022780669 | 30.21210674 |
| Saturn | 0.014059868 | 9.660859203 |
| Uranus | 0.024937228 | 31.68063158 |
| Neptune | 0.037406723 | 61.26999625 |
| Pluto | 8.642419355 | 16074.55597 |
| Density of surface materials | ||
Gas Planet; Angular Velocity
The above 'Δ' and 'ω₂' values for the gas planets are based upon the outside diameter and spin-rate of their gas-clouds, not the planets. They are therefore incorrect.
The correct 'Δ' values for our gas planets are likely to be somewhere between that for the earth (0.334) and that for our sun (0.319) dependent upon the planet's temperature.
Therefore, their spin-rates are likely to be less than the above gas cloud spin-rates.
Because we know the mass of these planets, we can estimate their planetary spin-rates (ω₂) based upon reasonable assumptions for planet average density and 'Δ':
| Gas Planet | mass [kg] | Radius [m] # | J [kg.m²] # | δKE [J] | R (m) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Jupiter | 1.89819E+27 | 4.405E+07 | 2.594E+41 | 3.132E+34 | 7.781E+11 | ||||
| Saturn | 5.6834E+26 | 2.947E+07 | 3.476E+40 | 5.518E+33 | 1.427E+12 | ||||
| Uranus | 8.6813E+25 | 1.575E+07 | 1.517E+39 | 3.594E+32 | 2.869E+12 | ||||
| Neptune | 1.02413E+26 | 1.665E+07 | 1.998E+39 | 6.982E+31 | 4.496E+12 | ||||
| Gas Planets Below Their Clouds # Based upon the following assumptions; Δ = 0.325 & ρₐᵥₑ = 5300 (kg/m³) |
|||||||||
From the above corrected values for the properties of the gas planets in our solar system, we can estimate their angular velocities:
| Gas Planet | E₁ [J] | E₀+E₃ [J] | E₂ [J] | ω₂ (##) [ᶜ/s] | |||||
|---|---|---|---|---|---|---|---|---|---|
| Jupiter | 1.004E+26 | -2.978E+31 | 2.978E+31 | 1.084E-05 (1.759E-04) | |||||
| Saturn | 2.355E+24 | -2.044E+30 | 2.044E+30 | 1.175E-05 (1.638E-04) | |||||
| Uranus | 1.084E+22 | 7.118E+28 | -7.118E+28 | -9.686E-06 (-1.012E-04) | |||||
| Neptune | 9.570E+20 | -6.203E+29 | 6.203E+29 | 2.492E-05 (1.083E-04) | |||||
| Angular Velocity of the Gas Planets (## angular velocity of the gas cloud) |
|||||||||
As you would expect, the planet's gas clouds are spinning faster than the planets themselves. This is the reason for the apparent activity in their gas-clouds.
Mathematical Symbols & Units
A mass (m) orbiting a force-centre will generate a positive kinetic energy (KE) and a negative potential energy (PE) between the force-centre and the orbiting body. The sum of the two is Newton's combined energy (E). Refer to Laws of Motion.
The potential energy (PE) between two or more bodies is also gravitational energy.
'δKE' is the difference between the kinetic energies of a satellite at its perigee and its apogee {J}
i.e. δKE = KEᴾ - KEᴬ
'KEᴾ' is the kinetic energy of a satellite at its perigee {J}
'KEᴬ' is the kinetic energy of a satellite at its apogee {J}
'PEᴬ' is the potential energy between a force centre and its satellite at its apogee {J}
'θ' is the angle of inclination of a satellite's orbital plane relative to its own plane orbital plane {radians}
'E₁' is the spin energy induced in a satellite by its force-centre {J}
'E₂' is the total spin energy in a satellite {kg.m²}
'E₃' is the spin energy induced in a satellite by its secondary satellite(s) {kg.m²}
'Eₒ' is the natural spin energy in a satellite induced by its own orbit {kg.m²}
'ω₁' is the angular velocity induced in a satellite by E₁ {J}
'ω₂' is the total angular energy in a satellite induced by E₂ {kg.m²}
'ω₃' is the total angular energy in a satellite induced by E₃ {kg.m²}
'ωₒ' is the total angular energy in a satellite induced by Eₒ {kg.m²}
'J' is the polar moment of inertia of a body {kg.m²}
'tₒ' is the satellite's orbital period
'tₛ' is the satellite's spin period
'r' is the satellite's radius
'R ' is the average orbital distance between the centre's of a satellite and its force-centre
'Δ' radial modifier (factor) for the polar moment of inertia of a rotating body
'₁' refers to the primary force-centre (star)
'₂' refers to the secondary force-centre (planet)
For the purposes of this document, the terms 'rotational' and 'angular' are interchangeable; all such velocities shall be interpreted has having magnitude and direction.
Refer to Laws of Motion for a detailed explanation of Newton's laws of planetary motion and Solar System Orbits for planetary orbit details
Definitions
The bodies are defined in Fig 1 according general understanding. However:
1) A force-centre can be galactic, solar or planetary, which may have their own satellites
2) A satellite can be solar, planetary or lunar, which may have their own secondary satellites
Further Reading
You will find further reading on this subject in reference publications(55, 60, 61, 62, 63 & 64)