Earth's Atmospheric Gases (the theory)
It is possible to accurately calculate the properties of the individual gases in the earth's atmosphere using well known and proven theories provided we accept the following reasonable assumptions:
1) Newton's law of gravitational attraction applies to the earth's atmospheric gases, making gravity their container
2) Dalton's law applies to all atmospheric gases
3) The average pressure of the combined gases in the earth's atmosphere (air) at sea level is 1.0 atmosphere (10332294.1352185g/m²)⁽¹⁾
4) The temperature profile for the earth's atmosphere at the poles is as shown in Fig 2 and reaches a maximum of 1206K⁽²⁾. Atmospheric temperature at the equator is ≈90K higher than at the south pole
5) Nitrogen constitutes 78% of the total mass of the earth's atmospheric gases at sea level⁽³⁾
6) Oxygen constitutes 21% of the total mass of the earth's atmospheric gases at sea level⁽³⁾
7) Argon constitutes 0.93% of the total mass of the earth's atmospheric gases at sea level⁽³⁾
8) CO₂ constitutes less than 0.038% of the total mass of the earth's atmospheric gases at sea level⁽³⁾
9) The practical ceiling for any atmospheric gas is the point at which 1 molecule of the gas concerned exists for each square metre at that altitude⁽⁴⁾
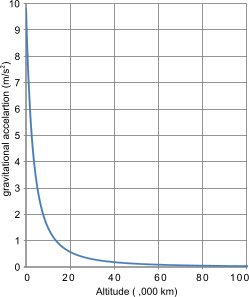
Fig 1. Earth's Gravity vs Altitude
Calculation Procedure {© 06/07/14}
Assumption 1):
Fig 1 shows the variation in the earth's gravitational acceleration with altitude.
Assumption 2):
Dalton's law states that all the gases in a mixture of gases behave independently and should therefore be considered and analysed separately. You can easily calculate the partial pressure of each gas in the earth's atmosphere as follows:
Given that we know the density of air (ρₐᵢᵣ) at sea level is approximately 1292.8g/m³, the principal properties for each component gas at sea level are ...
[units are evaluated to corroborate the formulas]:
The molecular density of air (ρᴹₐᵢᵣ) = ρₐᵢᵣ ÷ Σρᴹₓ.RAMₓ [g/m³ ÷ % x g/mole = mole/m³]
The molecular density of each gas (ρᴹₓ) = % . ρᴹₐᵢᵣ (mole/m³)
and the mass density of each gas (ρₓ) = ρᴹₓ . RAMₓ [mole/m³ x g/mole = g/m³]
Air pressure (pₐᵢᵣ) is 101325N/m²
Gas pressure (pₓ) = % . pₐᵢᵣ (N/m²)
Gas mass pressure (pmassₓ) = pₓ . (r+H)² ÷ G . m₁ [N/m² x m² ÷ N.m²/kg² x kg = kg/m²]
which is the mass of gas in the atmospheric column and 'H' is the altitude of its centre of mass
i.e. 50% of the mass lies above this altitude and 50% of the mass lies below it
To conclude for the principal gases in the earth's atmosphere @ 273.15K:
| gas | RAM | percentage | mole density | mass density | mass pressure |
|---|---|---|---|---|---|
| g/mole | ≈% | (ρᴹₓ) mole/m³ | (ρₓ) g/m³ | (pmassₓ) g/m² | |
| N₂ | 28.0134 | 78.087% | 34.42594855 | 964.387867 | 15821482.7 |
| O₂ | 31.9988 | 20.95% | 9.236154828 | 295.5458711 | 4244726.93 |
| Ar | 39.948 | 0.93% | 0.410005918 | 16.37891643 | 94215.7723 |
| CO₂ | 44.095 | 0.03% | 0.013225997 | 0.583200354 | 3104.60026 |
| Ne | 20.1797 | 0.0018% | 0.00079356 | 0.0160138 | 182.352182 |
| He | 4.002602 | 0.00052% | 0.000229251 | 0.000917599 | 52.6795176 |
| CHₓ | 16.04246 | 0.0002% | 8.81733E-05 | 0.001414517 | 20.71372 |
| H | 1.00794 | 0.000048% | 2.11616E-05 | 2.13296E-05 | 2.44097454 |
| N₂O | 44.0128 | 0.00005% | 2.20433E-05 | 0.000970189 | 5.17433 |
| O₃ | 47.9982 | 0.000004% | 1.76347E-06 | 8.46432E-05 | 0.41391 |
| H₂O | 18.01528 | 2% | 0.881733158 | 15.88466972 | 207137.22427 |
| Air # | 29.324 | 101.99962% | 1292.8 | 10563407.45 |
# 99.99962% air including 2% water
0.00038% trace elements are ignored
Conclusion for the earth's atmosphere @ 273.15 K (including 2% water):
mole density: ρₘₒₗₑ = ρₐᵢᵣ ÷ RAMₐᵢᵣ = 1292.8 ÷ 29.324 = 44.08666 moles/m³
composite atomic mass: mₐᵢᵣ = 4.90742335218544E-26 kg
mass density: ρₐᵢᵣ = 1.2928 kg/m³
inter-atomic separation: dₐᵢᵣ = √[ mₐₜₘ/ρₐₜₘ ] = 3.36078497740489E-09 m
inter-atomic force: Fₐₜₘ = pₐᵢᵣ.dₐᵢᵣ² = 1.17004808390491E-12 N
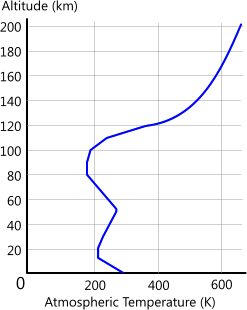
Fig 2. Atmospheric Temperature Profile
Incorporating the ideal gas law; p.V = n.Rᵢ.Ṯ
where:
p = pressure = force ÷ area (F/A)
V = volume
n = number of moles of substance
Rᵢ = ideal gas constant
Ṯ = temperature (absolute)
into the equation (F = G . m₁ . m₂ / (r+H)²) we can calculate altitude 'H' as follows:
F/A . V = n . Rᵢ . T
F = n . Rᵢ . T . A / V
F = n . Rᵢ . T / H (H = V/A)
If m₂ = n.RAM/1000 kg, then ...
F = G . m₁ . n.RAM/1000 / (r+H)²
n . Rᵢ . T / H = G . m₁ . n . RAM / 1000 / (r+H)²
Rᵢ . T / H = G . m₁ . RAM / 1000 / ( r² + 2rH + H²)
(r² + 2rH + H²) = H . G . m₁ . RAM / Rᵢ / T / 1000
H² + H.(2r - G . m₁ . RAM / Rᵢ / T / 1000) + r² = 0
a = 1
b = 2r - G . m₁ . RAM / Rᵢ / T / 1000
c = r²
H = {-b-√(b² - 4.a.c)} / 2a
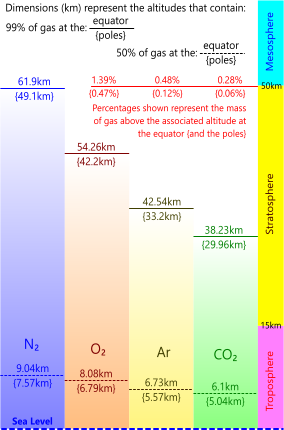
Fig 3. Earth's Atmospheric Gases @ Altitude
By entering the correct altitude temperature for the latitude and additionally modifying for the effects of centrifugal force (v²/r) you will find the correct value for 'H' for each atmospheric gas.
Repeat this procedure for the uppermost 50%, modifying m₁ and r to include the gas below 'H', and you will find H for the upper 50% in the gas column. Keep going (for the uppermost 25%, 12.5%, 6.25%, etc.) and you will discover how the mass pressure of gas varies with altitude.
Conclusion
From the above formula CalQlata has demonstrated that ...
'For any atmospheric gas with the same RAM at a given temperature, the altitude of a specified percentage of its total mass will always be identical '
Therefore irrespective of the total mass of a particular gas in the atmosphere, for any given temperature; its "percentage mass vs altitude" profile will not change.
Fig 3 shows the results from this calculation for the principal gases in the earth's atmosphere at the equator and the {poles}. Whilst weather patterns in the Troposphere will alter these theoretical pressures and densities locally, such variations will not alter the overall picture.
Using the same calculation procedure, we also generated 'mass pressure-altitude' plots for each gas (Fig 8), providing the mass of gas above the altitude in question.
Atmospheric Gas Ceilings
The following are CalQlata's practical and theoretical ceilings⁽⁴⁾ for each gas in the earth's atmosphere at the equator and the poles:
| ceiling (km) | practical | theoretical | ||
|---|---|---|---|---|
| Gas | equator | poles | equator | poles |
| N₂ | 3998.95038 | 3458.49594 | 8103.50773 | 7031.05161 |
| O₂ | 3118.26617 | 2665.80287 | 6204.52442 | 5386.80279 |
| Ar | 1985.51194 | 1647.63729 | 4008.86933 | 3462.06235 |
| CO₂ | 1525.38322 | 1236.35231 | 3215.26978 | 2753.62086 |
| O₃ | 991.62283 | 776.08888 | 2378.94412 | 2001.80321 |
| CF₂Cl₂ | 159.34693 | 107.41656 | 459.18917 | 327.51499 |
The top of the Exosphere is generally accepted as the upper limit of the earth's atmosphere and for all practical purposes this may well be the case as it is difficult to consider 'a few molecules per cubic meter' constituting a viable atmosphere, but for the purposes of theoretical calculations even such low densities as these should not be ignored.
Therefore, CalQlata set out to define the actual quantities of each gas in the earth's atmosphere, and according to our calculations, there remains 14624.816171kg of nitrogen, 30.753837772kg of oxygen and traces of Argon and other gases (hydrogen helium, etc.) above the top of the Exosphere.
Altitudinal Variation
Figs 4A to 4D show the properties of Earth's atmosphere as it varies with altitude.
These values are theoretical, based upon the above Calculation Procedure for 99.96% of the earth's atmospheric atoms (N₂, O₂ & Ar), and whilst they include the effects of,
1) altitudinal temperature,
2) gravitational variation above and at the earth's surface at the poles and the equator (Fig 1),
3) centrifugal force in the atmospheric atoms induced by the earth's rotation;
they do not include the effects of,
A) humidity (add 2% for 100% humidity & 0% for zero humidity),
B) ground elevation (mountains),
C) localised weather.
Pressure:
Figs 4A and 4B show how Earth's atmospheric pressure varies with altitude.
The reason for lower pressures at the equator, despite lower gravitational effect and higher atmospheric column are mostly due to the centrifugal force in the atmospheric atoms, which is absent at the poles; however, take a look at Pressure vs Density below.
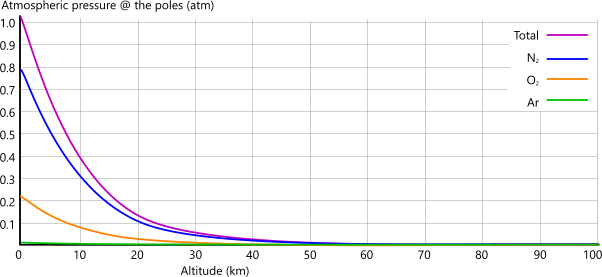
Fig 4A show this variation above sea-level at the earth's poles.
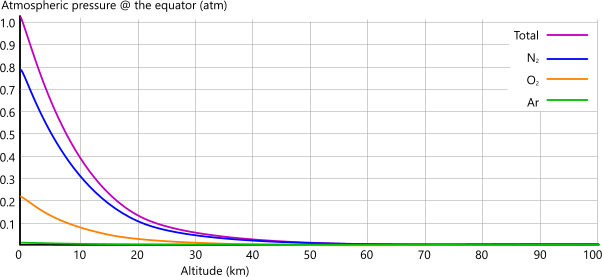
Fig 4B show this variation above sea-level at the earth's equator.
Density:Figs 4C and 4D show how Earth's atmospheric density varies with altitude.
The reason for lower densities at the equator are similar to those provided above for atmospheric pressure, but temperature has a significantly greater effect on the density of gases that are contained only by gravity. But why! I hear you cry. Take a look at Pressure vs Density below.
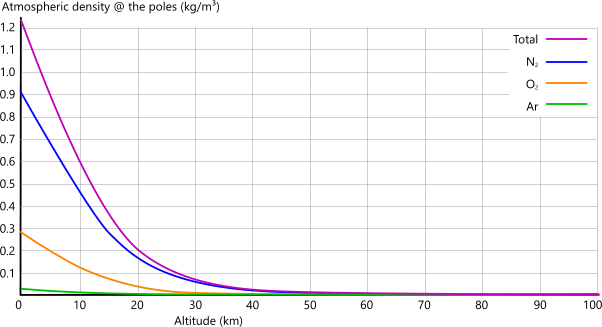
Fig 4C show this variation above sea-level at the earth's poles.
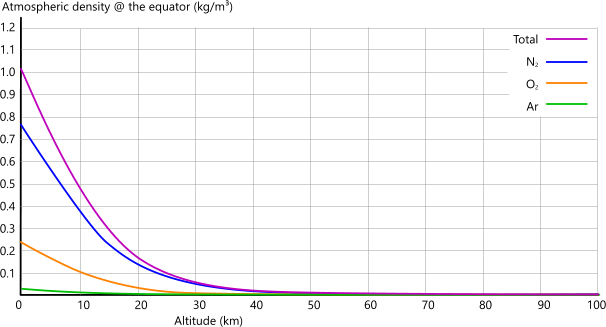
Fig 4D show this variation above sea-level at the earth's equator.
You will see recorded pressures and densities that differ slightly to the above.
This is because the above values are theoretical. And whilst recorded values are actual, they are only valid for the period over which they are taken.
Pressure vs Density:
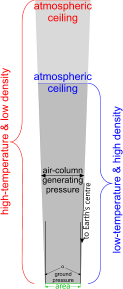
Fig 5. Pressure vs Density
Looking at Fig 5, it isn't difficult to see why temperature has a greater effect on the density of our atmosphere than it does on its pressure. This is due to the fact that dimensional variations in density normally apply in 3-D; but in atmospheric gases, all three dimensional effects act in one direction.
The earth's atmosphere is a mixture of unconstrained gases; gravity is their container. Therefore, their expansion and contraction with temperature variation is also unconstrained.
However, whilst these gases vary dimensionally with changes in temperature, their masses don't; they remain constant. This is one of the principal reasons - centrifugal force being the other - why the earth's atmospheric ceilings are significantly different at the poles and the equator but their pressures are similar.
The electrical charge between adjacent atomic protons (e') rises and falls with temperature, varying the repulsion [force], and therefore the distance between them. This repulsion is the cause of pressure variation in confined gases.
Whilst the earth's atmospheric gases are not confined, their only direction of unconstrained movement is upwards, amplifying the changes in ceiling-height as their densities alter with varying temperature. But, because the air column mass doesn't change, the ground pressure remains the same# irrespective of temperature.
# In reality, ground pressure does vary with temperature, but only slightly. The only two things affecting ground pressure with temperature are; column mass, which varies very slightly due to; 'α' (Fig 5), and gravitational acceleration (g), which varies little over this altitude range.
The following Table, which is based only upon the practical ceiling of the nitrogen gas in our atmosphere, offers an empirical example of the relative effect of temperature on its pressure and density. These calculations ignore the effects of centrifugal acceleration for reasons of clarity.
| Fig 5 | Poles | Equator |
|---|---|---|
| α (°) | 7.86565E-08 | 7.83928E-08 |
| ceiling (m) | 3458495.9 | 3998950.38 |
| volume (m³) | 4462157.761 | 5521506.879 |
| density (kg/m³) | 1.168782538 | 1.446260121 |
| pressure (kg/m²) | 49051483.06 | 45835100.83 |
| Atmospheric gas; nitrogen Area = 1m² |
The difference between the effects of temperature on atmospheric pressure and density can be seen quite clearly in the above Table, where despite a ceiling ratio of 1.1563;
air column density varies by a factor of 1.2374,
whilst,
air column pressure varies by a factor of only 1.0702.
The reason for this apparent anomaly is because no matter how much you raise the temperature of an unconstrained (other than by gravity) gas, its column mass remains largely unchanged, whilst its unidirectional density variations will alter according to PVRT amplifying the increase or decrease in the height of the air-column.
Atmospheric Heat:
Earth's atmospheric heat originates from two principal sources of EME radiation; [heat] energy generated by its own internal spin and that received from its stellar force-centre (sun).
We know that ...
... the total energy generated by Earth's internal spin is 2.87709E+28 J (most of which is lost in friction),
... the heat energy held by the planet's atmosphere @ 273K is approximately 5.11E+21 J/K,
... the minimum surface temperature of the earth (at the south pole) is ≈210K,
Note: the temperature at the north pole is not representative as it is warmed by the ocean currents.
We also know the earth's distance from the sun at winter and summer; 1.47095E+11m & 1.520942E+11m respectively.
These stellar distances result in the sun's heat being distributed over spherical surface areas; 2.718978E+23m² & 2.906934E+23m² respectively.
From the above we can estimate the [heat] energy the earth's atmosphere receives from internal spin and that received from stellar radiation.
The temperature at the earth's latitudes above and below its equator will also vary with the tilt presented to its sun.
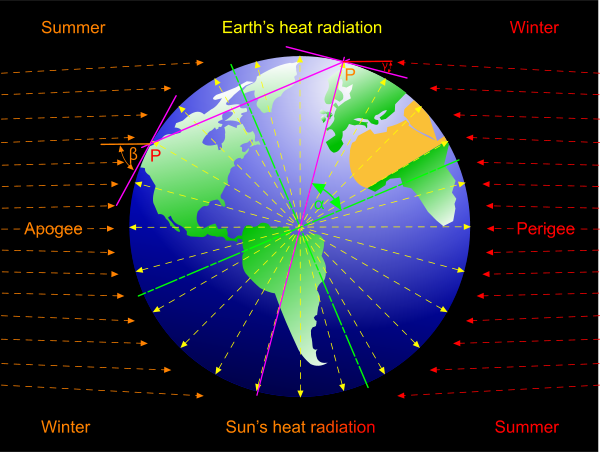
The following is an estimate of our sun's [radiated] contribution to Earth's surface [ground] temperature (Fig 6).
Assuming the following input data:
Earth's [spin axis] tilt: θ = 23.5°
Earth's perigee distance; Rᴾ = 1.470950E+11 m
Earth's apogee distance; Rᴬ = 1.520942E+11 m
Earth's contribution from its own internal heat: Ṯₒ = 237.15K (Est.)
The sun's maximum radiated temperature at the surface of the earth; Ṯₛ = 69K (Est.)
We can calculate the following:
The spherical area (A = 4πR²) at the earth's ...
... perigee; Aᴾ = 2.718978E+23 m²
... apogee; Aᴬ = 2.906934E+23 m²
The difference between the two areas is therefore;
δA = (Aᴬ-Aᴾ) / Aᴾ = 6.9%
Because the earth is currently closer to the sun during the northern-hemisphere's winter, the quantity of heat received by the earth's northern hemisphere during winter is 6.9% greater than during summer.
Because the surface-slope projected towards the sun is greater during the northern hemisphere's summer (β>γ), the quantity of radiated heat (per unit area) is greater in the northern-hemisphere during summer than during winter.
At any latitude (α), the heat received 'per unit area' will vary according to the following.
| Northern Hemisphere: | |
|---|---|
| Winter | Summer |
| γ = π/2-α-θ | β = π/2-α+θ |
| Southern Hemisphere: | |
| γ = π/2-α+θ | β = π/2-α-θ |
Therefore, the earth's average# surface temperature - as a result of stellar radiated heat energy - at any particular latitude may be estimated thus:
Winter; Ṯʷ = Ṯₛ.Sin(γ) + Ṯₒ
Summer; Ṯˢ = Ṯₛ.Sin(β) + Ṯₒ
# during a 24-hour period (colder during the night and warmer during day)
The following locations have been selected to minimise the influence of; weather, oceans, [ground] elevation, atmospheric heat transfer, etc.
| Location | Ṯʷ (°C) | Ṯˢ (°C) |
|---|---|---|
| Northern Hemisphere: | ||
| Irkutsk (Lat. 52°) | -18.7 | 20.4 |
| Yakutsk (Lat. 62°) | -30.6 | 14.3 |
| Tazirbu (Lat. 23°) | 11.0 | 28.2 |
| Southern Hemisphere: | ||
| Equator (Lat. 0°) | 22.9 | 27.3 |
| Antarctic (Lat. 90°) | -63.5 | -10.4 |
| Winter (Ṯʷ) and Summer (Ṯˢ) Temperatures at the Earth's Surface Ṯₒ and Ṯₛ are estimates, selected to provide best-fit surface temperatures for various representative locations on the earth's surface (see above). Whilst they might be improved through manipulation, improvement is difficult with alterations greater than ±1K. Therefore, we can be fairly confident (±1%) that ≈90K (27.3°C - -63.5°C) of our sun's radiated temperature reaches the earth's surface when orbiting at its perigee. |
||
Because the comparative data that could be found for these regions is similar to that quoted in the above Table, the values for Ṯₒ and Ṯₛ may be considered representative. But this raises the question;
"what stellar energy is required to generate Ṯₛ?"
It is important to understand that some of the earth's atmospheric heat energy is collected from the sun's radiated EME (Ṯₛ) and the remainder is provided by Earth itself (internal heat; Ṯₒ). From the relative values of Ṯₒ and Ṯₛ, we can deduce that ≈70% of the earth's atmospheric heat comes from within.
The sun's spin-friction energy has been calculated (by CalQlata) as: δEₛ = 1.61E+35 Joules
some internet estimates appear to favour 1.20E+34 Joules, but its origin and reliability are unknown.
Because the sun's internal heat from spin-friction is sufficient to initiate fission in its core matter, its total energy (E) will be significantly greater than that generated by spin-friction alone (E>δEₛ).
Because the lowest [static] temperature of the earth's atmosphere at its surface is ≈210K and the highest [static] temperature is ≈300K (273+27), we also know that the heat trapped (held) by the earth's atmospheric molecules is generated as follows:
internal spin: Ṯᵢ = 5.11E+21 x 210/300 = 3.577E+21 Joules/Kelvin
stellar radiation: Ṯₛ = 5.11E+21 x 90/300 = 1.533E+21 Joules/Kelvin
The source of the earth's surface [heat] energy:
Spin theory tells us that the internal energy generated by our sun is 1.606E+35 Joules.
Like all stars, ours is a large, highly energised gas planet. So its viscous matter is smaller than the volume we see.
Before it collected its planetary bodies (from galactic comets), our sun comprised the same matter as all other large celestial bodies. Given its known mass of 1.9885E+30 kg, and its original density (≈5500 kg/m³), its radius is probably about 442,000 km (63.5% of the visible star), the remainder (its atmosphere) being hydrogen and helium gas. This would mean that its viscous volume is about 333,958 times larger than the earth.
Given the following reasonable assumptions:
Earth ...
... density: 5506.35132682682 kg/m³
... average radius: 6367444.5 m
... surface area: 5.09494E+14 m²
... spin energy: 2.87702E+28 J
... average orbital radius: 1.49595E+11 m
... average spherical orbital area: 2.81217E+23 m²
... atmospheric mass: 5.28951E+18 kg
... atmospheric SHC: 965.3923863 J/kg/K (based upon the earth's principal atmospheric gases; N₂, O₂, Ar)
... ocean density: 1025 kg/m³
... ocean SHC: 919 J/kg/K
... %age area oceans: ≈70%
... %age area land: ≈30%
... land density: ≈2000 kg/m³
... SHC land: ≈4000 J/kg/K
Sun ...
... density: ≈6000 kg/m³
... radius: 695710000 m
... mass: 1.9885E+30 kg
... surface area: ≈6.0822793E+18 m²
... spin energy: 1.60602E+35 J
we should be able to determine their respective heat contributions (Earth and Sun).
The above values preceded with '≈' are estimates. The other values are known.
Before estimating the sun's radiated energy, it is necessary to determine how much of the earth's surface heat is generated by its own internal spin-friction. We can set this datum at the South Pole in mid winter at ≈210 K.
In the following Table, the values in blue are input estimates, and those in red are known input values (the remainder are calculated):
| atmosphere: | Earth (contribution) | Sun (contribution) | |
|---|---|---|---|
| temperature | 210 | 90 | K |
| energy | 1.07236E+24 | 4.59581E+23 | J |
| oceans: | |||
| heated depth | 3700(a) | 1000 | m |
| temperature | 276 | 7.35(b) | K |
| volume | 1.31959E+18 | 3.56647E+17 | m³ |
| mass | 1.35258E+21 | 3.65563E+20 | kg |
| energy | 1.02441E+27 | 2.46925E+24 | J |
| 70% | 70% | ||
| land: | |||
| heated depth | 11000(c) | 111(d) | m |
| temperature | 331 | 79 | K |
| heated volume | 1.68133E+18 | 1.69662E+16 | m³ |
| heated mass | 3.36267E+21 | 3.39324E+19 | kg |
| energy | 4.45217E+26 | 1.07226E+24 | J |
| Total: | 1.4707E+27 | 4.00109E+24 | J |
| ratio of areas | 114667.5085 | ||
| surface heat energy | 4.58795E+29 | J | |
| friction energy: | 2.72995E+28 | 1.53218E+35 | J |
| %age friction: | 94.88810% | 95.40252% | |
| The above figures show the relative heat energy contribution from the earth's internal spin-friction and our sun's radiated EME. Percentage spin-energy expended as friction - the remainder is radiated in the form of heat. The blue input values are estimated as follows: (a) the average depth of all of the earth's oceans (b) the degrees of temperature (above 276K) of the upper 1000m of the earth's oceans (c) the average depth of the earth's continental crust (d) the absolute minimum average depth of the earth's permafrost; optimised with (b) above to ensure 70% energy contribution over the earth's oceanic surface |
|||
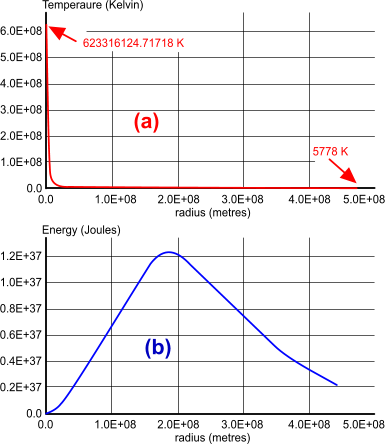
Fig 7. Solar Energy
Assuming that our sun is approximately 334,000 times larger than the earth, and that both celestial bodies originally comprised similar matter, it may be expected that its internal frictional energy will be similarly greater; i.e.; 1.53218E+35 Joules (the sun's calculated spin energy is 1.60602E+35 Joules). Moreover, the profusion of hydrogen (H) and helium (He) at the sun's surface, confirms that fission is being generated at its core, which means that its core temperature must be neutronic; neutrons are being created. However, given the sun's core temperature of 6.233E+08K (Fig 7; a), and its SHC of ≈470 J/K/kg, its total energy must be ≈5E+36 Joules (Fig 7; b), which compares favourably with the detailed calculations for our sun (4.66E+36J), and is considerably more than that generated through spin alone.
This additional energy comes from core-fission and is responsible for the star's energy storage; neutron generation.
To summarise, our sun ...
... radiates ≈1.09E+33 Joules of energy.
... contributes ≈5.0E+23 Joules of energy to the earth's atmospheric heat.
... generates ≈1.606E+35 Joules of internal spin friction energy.
... generates ≈4.5E+36 Joules from fission (29 x spin).
Escape Altitude
Escape altitude is the altitude (H) at which centrifugal acceleration is equal to gravitational acceleration.
H = 35,843.42548km
Any object orbiting the earth whilst remaining over the same point of its surface would escape the earth's gravitational attraction if it exceeded the escape altitude. Moreover;
If it travels faster than the earth's rotation at the escape altitude the object will fly off into space.
If it travels slower than the earth's rotation at the escape altitude the object will fall to earth.
Because we know that the earth's atmospheric gases above the Troposphere will never travel faster than the earth's rotation and that the highest atmospheric gas molecule is below the escape altitude, we also know that;
"none of the earth's atmospheric gases can be lost to space due to centrifugal force"
This statement can be proven mathematically with respect to today's atmosphere as follows:
Comparing the earth's gravitational attraction on each atmospheric gas molecule with its centrifugal force at its theoretical ceiling today (see Atmospheric Gas Ceilings above), we can deduce the following:
| molecule | RAM | m | H | R | Fᵍ (+ve) | v | Fᶜ (-ve) | F |
|---|---|---|---|---|---|---|---|---|
| (kg) | (km) | (m) | (N) | (m/s) | (N) | (N) | ||
| N₂ | 28.0134 | 4.69E-26 | 8103.5 | 1.448E+07 | 8.89E-26 | 1053.1 | -3.59E-27 | 8.53E-26 |
| O₂ | 31.9988 | 5.35E-26 | 6204.52 | 1.26E+07 | 1.34E-25 | 915.04 | -3.56E-27 | 1.31E-25 |
| Ar | 39.948 | 6.68E-26 | 4008.9 | 1.04E+07 | 2.46E-25 | 755.37 | -3.67E-27 | 2.43E-25 |
| CO₂ | 44.01 | 7.36E-26 | 3215.3 | 9.59E+06 | 3.18E-25 | 697.65 | -3.74E-27 | 3.14E-25 |
| O₃ | 47.998 | 8.03E-26 | 2378.9 | 8.757E+06 | 4.163E-25 | 636.84 | -3.718E-27 | 4.13E-25 |
| CF₂Cl₂ | 120.91 | 2.02E-25 | 459.19 | 6.84E+06 | 1.72E-24 | 497.23 | -7.31E-27 | 1.71E-24 |
| proton | 1 | 1.67E-27 | 8103.5 | 1.45E+07 | 3.172E-27 | 1053.14 | -1.28E-28 | 3.043E-27 |
Gravitational force is lowest and centrifugal force is greatest in a gas at its ceiling. So if the resultant force (F) for all gases are positive (in the above Table) at their atmospheric ceilings it means that no molecule can escape the earth's gravitational attraction due to centrifugal force. This point is reinforced by the hypothetical case for a proton at the ceiling for nitrogen.
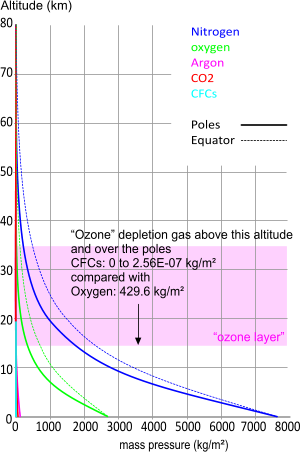
Fig 8. Earth's Gases vs Altitude
Given that the earth's atmosphere is unlikely ever to have contained sufficient quantity of any gas to have achieved a ceiling at the earth's escape altitude (35,840km)⁽⁹⁾, the above Table confirms that no part or type of any atmospheric gas has ever been thrown into outer-space as a result of centrifugal force.
The "Ozone Layer"
The Ozone layer is said to exist in the Stratosphere between altitudes 15km and 35km
Ozone
Ozone (O₃) is an unstable molecule generated by oxygen molecules (O₂) picking up stray oxygen atoms (O) that exist after the sun's electromagnetic radiation (UV) has split other oxygen molecules in two.
It is of course natural to expect that a greater percentage of the oxygen molecules present in the higher regions of the atmosphere, where they are closer to the radiation source, will be subject to ozone generation than at lower altitudes. However, it is also true that there is much more oxygen closer to sea level than at the higher altitudes (the "Ozone Layer" contains about 17.7% of the earth's oxygen). We know from countless practical experiments and the existence of 'sun-tan' that UV radiation reaches the earth's surface, meaning that ozone is generated naturally even at sea level and that it must be a feature of the entire oxygen layer, not just the region between altitudes 15km and 35km.
As the RAM of Ozone is 47.9982g/mole, making it heavier than O₂, and as gravity is its container, its natural home in the atmosphere is at a lower altitude than the oxygen molecule (see Fig 9). Therefore, whilst ozone is generated in the region popularly referred to as the "Ozone Layer", it is not where it wants to be. It will fall towards earth immediately it is created.
As the ozone molecule is unstable, during its fall it will encounter other oxygen atoms to which it will lose (donate) its unnatural oxygen atom.
Our atmospheric calculations (see Calculation Procedure above) also revealed a difference in elevation of 12.06km between the poles and the equator (42.2km & 54.26km respectively) in the 99%-oxygen altitude that some people believe represents a "Hole" in the "Ozone Layer" over the poles. Such a hole is impossible according to Dalton's law. This thinning of the oxygen layer over the poles is a natural phenomenon generated by the centrifugal force on the earth's atmosphere from its rotation about its polar axis. This thinning at the poles exists for all the earth's atmospheric gases, not just oxygen, and will always exist as long as the earth retains an atmosphere and continues to rotate about its own axis.
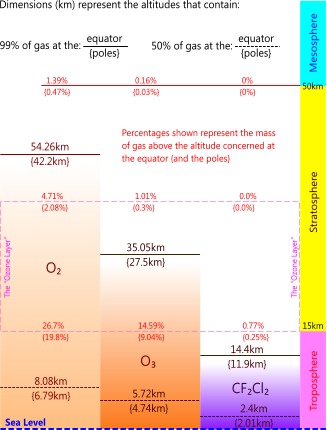
Fig 9. Earth's Ozone Related Gases
CFCs
Out of interest, we applied the CFC Ozone depletion argument recently used to explain a "Hole" in the "Ozone Layer" to see if there could have been sufficient CFC gas present in the region concerned to have a significant effect on the oxygen. As can be seen in Fig 8 CFCs can have affected no more than 0.00000006% of the O₃ molecules in the "Ozone Layer". Not only is this negligible, its effect would be greater over the equator than over the poles!
"Greenhouse" Effect
The "Greenhouse" effect is a reference to the ability of atmospheric gases to retain heat and thereby raise a planet's surface temperature, which would otherwise fall to that of outer-space; 2.7255K (Earth's surface temperature would, of course, fall to that generated by its own internal friction; ≈210K). The ability of any gas to retain heat energy is defined by its 'Specific Heat Capacity'.
Specific heat capacity (cp) is measured in J/kg/K (btu/lb/R) and describes how much energy a unit mass of the substance will require for each degree (K or R) of change in temperature.
If we know the mass of each gas in the earth's atmosphere, we can calculate the amount of heat energy stored in that gas and therefore its contribution to the "Greenhouse" effect.
The mass of each gas in the earth's atmosphere was established from their pressures in the above Calculation Procedure; and by multiplying the specific heat capacity by its mass we can determine the heat energy stored in each gas.
Whilst our calculation is valid for a particular temperature (273K), and the specific heat capacity of most gases rises with temperature (see The Atom below), the relative contribution from each gas in the earth's atmosphere will remain largely unchanged.
The following table lists the results from these calculations:
| Gas | cp | Mass | Stored Energy | %age of Air |
|---|---|---|---|---|
| J/kg/K | kg | J/K | ||
| N₂ | 983 | 4.13091006E+18 | 4.060684588E+21 | 79.5209485% |
| O₂ | 919 | 1.10774396E+18 | 1.018016698E+21 | 19.9359619% |
| Ar | 531 | 4.91366416E+16 | 2.609155669E+19 | 0.5109546% |
| CO₂ | 844 | 1.58453127E+15 | 1.337344390E+18 | 0.0261894% |
| Ne | 1030 | 9.50566787E+13 | 9.790837905E+16 | 0.0019174% |
| He | 5240 | 2.74608183E+13 | 1.438946878E+17 | 0.0028179% |
| CHₓ | 2200 | 1.05618532E+13 | 2.323607701E+16 | 0.0004550% |
| H | 14300 | 2.53484477E+12 | 3.624828014E+16 | 0.0007099% |
| N₂O | 880 | 2.63837434E+12 | 2.321769416E+15 | 0.0000455% |
| (H₂O) | (1859) | (1.05618532E+17) | (1.963448508E+20) | |
| Totals | 5.28951345E+18 + H₂O | 5.106433796E+21 + H₂O | 100% + H₂O |
The stored energy values in the above table assume that all the atmospheric gases are at 273K, which is not correct. Temperature drops and rises with altitude (see Fig 2) and the heat capacity of all gases rise and fall with temperature, not necessarily at the same rate but very similarly, except where certain gases fade out at various altitudes, the total percentage contribution of stored heat is virtually identical no matter how you perform this calculation.
The temperature of the earth's atmosphere is directly proportional to the heat energy retained in its gases. Therefore, a change in the mass of any gas in the earth's atmosphere will have a consequential effect on the earth's surface temperature.
The 'Stored Energy' value in the above table (5.10643E+21 J/K) multiplied by 273.15 (1.39482E+24 J) represents the energy in the atmosphere that would be required to raise the temperature of all the gas molecules to 273.15 K.
Therefore, every single degree (1K or 1°C) of atmospheric temperature requires an additional 5.106433796E+21 J of heat energy. In other words, to raise the temperature of the atmosphere by 1K (to 274.15 K) you would need to increase the total Stored Energy by 5.106433796E+21 J.
To conclude;
It is clear from Spin Theory that ≈70% of the earth's atmospheric heat energy is [continually] generated by friction within its mantle (2.88E+28J), the remaining ≈30% comes from our sun.
Because nitrogen is responsible for 79.52% of the atmosphere's stored energy, a 1% change in its mass will significantly affect surface temperature.
On the other hand;
a significant increase (e.g. >1000%) in the mass of gases such as neon, carbon dioxide, helium, hydrogen that together constitute less than 0.039% of the atmosphere's stored energy will have very little effect on the earth's surface temperature.
However, if we apply the laws of thermodynamics to the above argument these effects are not quite so straight forward, for example; ...
CO₂
Along with other carbon gases, CO₂ is today charged with being the principal cause of Global Warming (see Global Warming below) because it is a "Greenhouse" gas. This claim is made because of its low specific heat capacity; i.e. it requires less energy input to raise its temperature by 1K than the more abundant atmospheric gases (except argon). However, its contribution to the earth's atmospheric temperature can only be considered in conjunction with its relative mass.
Applying the specific heat equations to each gas in the earth's atmosphere reveals the following relationship between CO₂ and its effect on earth's atmospheric temperature:
| Gas | cp | CO₂ | CO₂ x 0.9 # | CO₂ x 10 |
|---|---|---|---|---|
| J/kg/K | kg | kg | kg | |
| N₂ | 983 | 4.1309E+18 | 4.1309E+18 | 4.1309E+18 |
| O₂ | 919 | 1.1077E+18 | 1.1077E+18 | 1.1077E+18 |
| Ar | 531 | 4.9137E+16 | 4.9137E+16 | 4.9137E+16 |
| CO₂ | 844 | 1.5845E+15 | 1.4261E+15 | 1.5845E+16 |
| Ne | 1030 | 9.5057E+13 | 9.5057E+13 | 9.5057E+13 |
| He | 5240 | 2.7461E+13 | 2.7461E+13 | 2.7461E+13 |
| CHₓ | 2200 | 1.0562E+13 | 1.0562E+13 | 1.0562E+13 |
| H | 14300 | 2.5348E+12 | 2.5348E+12 | 2.5348E+12 |
| N₂O | 880 | 2.6384E+12 | 2.6384E+12 | 2.6384E+12 |
| Air: | mass: | 5.2895E+18 kg | 5.2894E+18 kg | 5.3038E+18 kg |
| cp: | 965.3882 J/kg/K | 965.3918 J/kg/K | 965.0618 J/kg/K | |
| Ṯ: | 293.7471 K | 293.7548 K | 293.0563 K |
As this is a constant in each calculation changing the energy input will not alter the relative results
Conservatively based upon the assumption that mankind generates 50% of the earth's CO₂: 0.9 = 90% = 50% + 50% x 80%
# The EU is claiming that Europe must reduce mankind's carbon emissions by 20% by 2020⁽⁵⁾. Even if a reduction of 20% was achievable, as can be seen from the above table it would have no noticeable effect on the earth's atmospheric temperature, other than to increase it slightly.
As can be seen in the above table, increasing the quantity of CO₂ actually decreases the temperature of the earth's atmosphere.
This phenomenon is due to the fact that the additional mass of the increased CO₂ in the atmosphere (CO₂: 1.585E+15 kg > 1.585E+16 kg) more than offsets the reduction in combined specific heat capacity of the gas mixture (air: 965.3882 J/kg/K > 965.0618 J/kg/K).
In fact increasing any gas in a mixture that contains a fixed amount of heat energy will cause the temperature of the mixture to drop as the energy is distributed over a greater number of molecules (refer to 'Heat').
For example, if 1kg of the earth's atmospheric mass holds 235156.5J of energy and has a temperature of 273K; increasing its mass by 1% with:
N₂ reduces the temperature of the gas mixture to 269.4K
O₂ reduces the temperature of the gas mixture to 270.6K
Ar reduces the temperature of the gas mixture to 272.0K
CO₂ reduces the temperature of the gas mixture to 270.9K
Therefore, simply increasing the earth's atmospheric CO₂ cannot increase its temperature.
However, if the entrained heat energy in the gas mixture is also increased by 2% (for each of the increases shown above):
N₂ increases the temperature of the gas mixture to 274.785K
O₂ increases the temperature of the gas mixture to 276.01K
Ar increases the temperature of the gas mixture to 277.4K
CO₂ increases the temperature of the gas mixture to 276.35K
clearly showing that Argon has a greater effect on atmospheric temperature than CO₂
The above increase in entrained heat (2%) along with the gas mass increase (1%) represents the following percentage increases for each gas in the mixture:
N₂ would need to increase by 1.28%
O₂ would need to increase by 5%
Ar would need to increase by 200%
CO₂ would need to increase by 2564.1%
proving that ...
only a small percentage increase in N₂ and O₂ is needed to raise the temperature of the earth's atmosphere by ≈3K,
almost double the amount of Ar is needed to achieve a similar rise in temperature,
but more than 26 times current levels of CO₂ are required to generate a similar rise in temperature.
The Atom
Notwithstanding the above calculations, which are based on generally accepted scientific theory, recent work on The Atom has demonstrated that all proton-electron pairs in all atoms and molecules collect and disperse electro-magnetic energy (heat) according to a basic mathematical rule that is fully in accordance with the theory of Heat. We are therefore able to replace the age-old 'PVRT' formula for the pressure of gases with others based upon the potential energies (PE), and therefore the kinetic energies, of the proton-electron pairs in any atom or molecule.
This rule allows us to predict (calculate) the specific heat of any atom at any temperature, revealing the following about our atmospheric gases.
For example; at 273.15K, the electro-magnetic energy (Joules) held by ...
... a single carbon atom (6 proton-electron pairs) is 6.5775623E-20 J,
... a single nitrogen atom (7 proton-electron pairs) is 7.026032422E-20 J,
... a single oxygen atom (8 proton-electron pairs) is 7.4745026E-20 J,
... a single argon atom (18 proton-electron pairs) is 1.01496626E-19 J,
giving us the following properties of the principle atmospheric gases in our atmosphere (@ 273.15K):
the N₂ molecule, which constitutes 78% of the earth's atmospheric gases, holds 2997368.6 Joules of heat energy per kilogram,
the O₂ molecule, which constitutes 21% of the earth's atmospheric gases, holds 2791456.5 Joules of heat energy per kilogram,
the Ar atom, which constitutes 0.93% of the earth's atmospheric gases, holds 1518177.0 Joules of heat energy per kilogram.
Whereas:
the CO₂ molecule, which constitutes <0.038% of the earth's atmospheric gases, holds 2922700.5 Joules of heat energy per kilogram.
The atomic model#, which also applies to CO₂, shows us that actually; CO₂'s heat capacity is slightly less than that of N₂, slightly more than that of O₂ and twice the capacity of argon at this temperature.
# The atmospheric gases each hold (and dissipate) electro-magnetic energy according to their proton-electron pair shell configuration.
Therefore, nitrogen traps (holds) more [heat] energy per unit mass than the other gases, and also constitutes the largest number of proton-electron pairs in our atmosphere. Argon on the other hand, traps the least (per unit mass), allowing more of the earth's own internal energy to escape the atmospheric molecules and more of the sun's radiated heat to reach the planet's surface.
The point raised here is that the same mathematical rule applies to the proton-electron pairs in all atoms whether or not they are part of a molecule; and that nitrogen, oxygen and argon together turn-over 2646 times as much atmospheric heat energy as carbon-dioxide.
When all said and done, our own calculations based upon thermodynamics, those based upon an evaluation of the sun's energy, and the recent work on the atom, all show us that CO₂ contributes very little to the earth's atmospheric heat.
Moreover, the earth's surface heat is provided by its own internal friction and solar energy. So simply removing a few of its atmospheric molecules (irrespective of the gas) without reducing its heat will simply raise the temperature of those that remain.
It is also important to understand that heat and temperature are not the same thing. There is less heat in a kilogram of iron than in a kilogram of boron, both of which are at the same temperature, because of the larger number of boron atomic shells in lower shell-numbers (i.e. at higher kinetic energies). This same argument applies to all atmospheric gases. So, one cannot simply claim that a higher temperature means more heat!
Counter-Arguments
The arguments against relating CO₂ to global warming are so numerous that it has been decided to move ours to a dedicated page and leave this page to the scientific facts.
Earth vs Venus (atmospheric comparison)
It is claimed that when both planets were young, say 1 billion years old, Earth and Venus were very similar and that Venus' runaway atmosphere was due to excessive CO₂.
It is also claimed that if the earth's CO₂ is allowed to rise just a few 10ᵗʰs of a percent above its current level, the earth's atmosphere could end up similar to that of Venus.
We have already shown that CO₂ cannot cause this problem on earth (see CO₂ above), but;
we have not shown the probable reason for Venus' atmospheric temperature.
Venus and Earth are respectively about 100 million km and 150 million km from the sun.
The sun's radiated energy is inversely proportional to the square of the distance from its surface.
The ratio of Venus' and Earth's respective energy budget from the sun is:
4.π.Rᵥ² ÷ 4.π.Rₑ² = Rᵥ² ÷ Rₑ² = 1.911
Venus therefore receives 1.911 times more of the sun's heat energy than does the earth
Given the thermodynamic equation Q = m.cp.Ṯ and the fact that both planets are claimed to have been similar in material and behaviour, m and cp may be ignored for their atmospheric properties (due to similarity), therefore; Ṯₑ ÷ Qₑ = Ṯᵥ ÷ Qᵥ from which, the sun's contribution to Venus' surface temperature is: Ṯₑ x Qᵥ ÷ Qₑ = Ṯᵥ = 1.911 x Ṯₑ
Today, the earth's surface temperature is less affected by the heat generated in its mantle where its crust is thickest, i.e. in its continents than through its sea floor.
Most of the sun's heat energy reaches the ground at the equator when the sun is at its highest in the sky (≈30°C), and the least of the sun's heat energy reaches the earth at its poles (≈-60°C).
Therefore the sun's heat must be responsible for generating the difference between the ground temperature at the equator and at the Antarctic (90K).
If the earth's ground temperature varies between 225K and 315K, the heat from the sun at Venus' equator must be 225K + 1.911 x 90K = 397K (124°C); i.e. higher than the boiling point of water at 1 atmosphere⁽¹⁾.
To this can be added the following facts:
Photographic and radiographic evidence of the surface of Venus shows that it has never had tectonic plates, which is a strong indication that it has never had the liquid surface water required for subduction#.
Earth's geological evidence shows it had liquid surface water 3.5bn years ago and the boiling temperature of water on Earth at that time was less than it is today (< 100°C) due to a much thinner atmosphere⁽⁹⁾ (< 1atm⁽¹⁾) therefore the earth's water temperature must have been considerably less than 100°C.
If Venus and the earth were both similar they must have supported similar quantities of water as the earth does today (≈1.386E+21kg⁽⁸⁾) and as it is not, and probably never has been, in liquid form on Venus' surface it must always have existed in vapour form in its atmosphere.
If all the water on Venus is gaseous the mass of its atmosphere must have been at least 258 times greater than that of the earth's atmosphere today (>258 atm; see CO₂ above) increasing the boiling point of water on Venus' surface to above 374°C (Venus' surface temperature is today ≈450°C)
# Because Venus has no continents its crust is equally thick over its entire surface and thinner than the earth's continental crust, therefore, Venus' mantle will have a greater effect on its surface temperature than on the earth where its thin crust is covered with deep water.
In conclusion, earth's atmosphere has never been similar to that of Venus and could not possibly degenerate to such a condition unless it moves considerably closer to the sun.
Global Warming
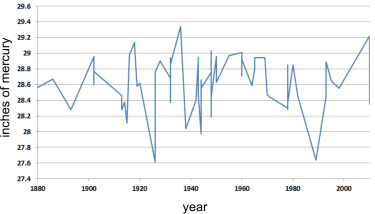
Fig 10. Air temperature records for 100 years
CalQlata has searched high and low for independent atmospheric temperature records that indicate a global trend upwards and found none.
For the purpose of clarification, we have plotted the records from one site⁽⁶⁾ for atmospheric pressure, which is directly related to temperature through the relationship PV=RT (Fig 10). It indicates no noticeable increase in temperature.
What is considerably more worrying, however, is that according to Milankovitch, we are about to enter into another ice-age.
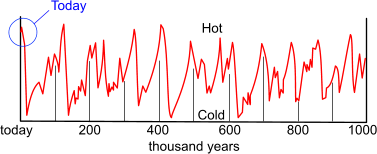
Fig 11. The Milankovitch Cycles
Milutin Milankovitch⁽⁷⁾ was a scientist of incredible vision and ability. He set out to prove a relationship between the earth's hot and cold cycles and the movements of the sun, moon and planets in our solar system and his theories have since been proven correct by studying the coral reefs on the Caribbean island of Barbados. This insight has given us the ability to predict and plan for future climatic events.
CalQlata has reproduced a simplified version of his graph of hot and cold periods simply to illustrate the point (Fig 11).
Notes
- 10332294.1352185g/m² = 1 atmosphere ≈ 14.7psi = 0.1N/mm² (CalQlata's UniQon)
- Whilst atmospheric temperature is included in the calculation procedure, the final calculation results appear to be relatively insensitive to significant variations. That is, alterations of up to 20% to the temperature vary overall altitudes and percentages by less than 1%
- www.space.com and reference publication 15
- CalQlata's practical ceiling is the altitude above which less than one molecure exists for each square meter of the atmospheric sphere and is based upon the fact that above this point there is no mass contributing to the column of gas generating atmospheric pressure at sea level.
CalQlata's theoretical ceiling is the altitude above which the theory cannot account for a single molecule of the gas concerned. - The Guardian
- originally @; https://www.wunderground.com/resources/pressure_records.asp?MR=1
- Milankovitch Cycles (osssociety.org)
- USGS statistics
- The two gases that constitute 99% of today's atmosphere (oxygen and nitrogen) were trace elements before plant life first ventured onto land around 350m years ago
Further Reading
You will find further reading on this subject in reference publications(12 & 15)