Steam (thermodynamic properties)

The following specific properties are for superheated steam, as opposed to saturated steam.
Superheated steam is water at a temperature greater than its boiling point at a designated pressure, i.e. all of the water will be gaseous.
Saturated steam is water at a temperature no greater than its boiling point at a designated pressure, i.e. not all of the water will be gaseous.

Steam (water vapour) is a gas. It will expand and compress with variations in pressure and temperature. Therefore you can apply the thermodynamic laws to its behaviour. From the following graphs⁽¹⁾, everything you need to know about the energy of steam can be calculated.
Example calculations are provided at the bottom of this page for various properties of steam at the specific pressure (60bara) and temperature (450°C) identified on each plot.

Specific Enthalpy

Specific enthalpy (h) is the total amount of energy 'per unit mass' in a substance that is available for work

h = u + p.V

Fig 1. Specific Enthalpy Chart for Superheated Steam

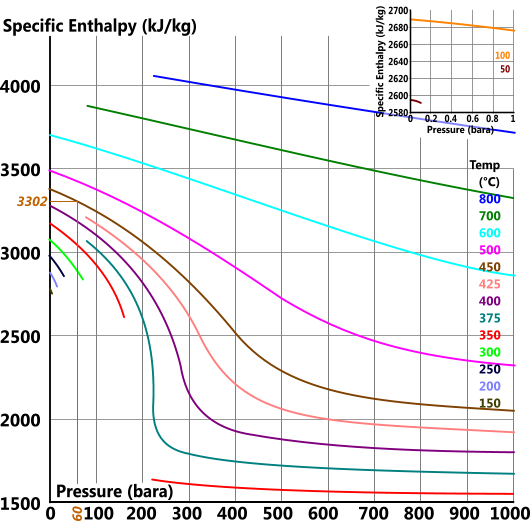
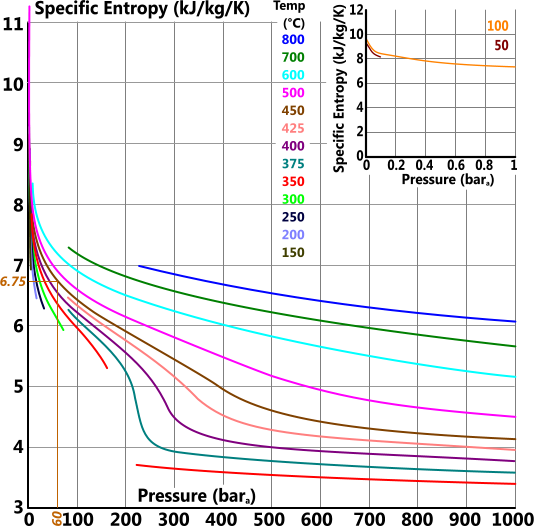
Specific Entropy

Specific entropy (s) is the fundamental energy 'per unit mass' of a substance (that cannot be converted into work).

s = h/T

Fig 2. Specific Entropy Chart for Superheated Steam

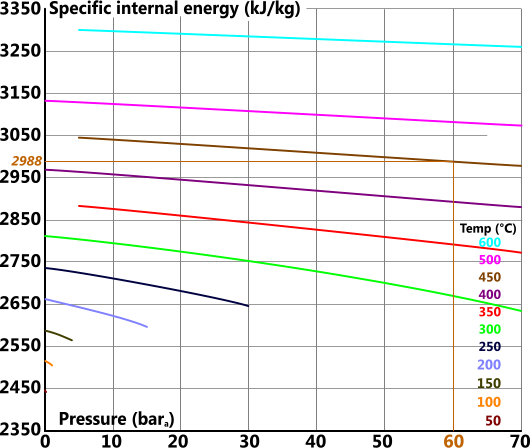
Specific Internal Energy

Specific internal energy (u) is the enthalpy per unit mass of a substance minus the energy 'per unit mass' that has been expended in doing work

u = h - p.V

Fig 3. Specific Internal Energy Chart for Superheated Steam

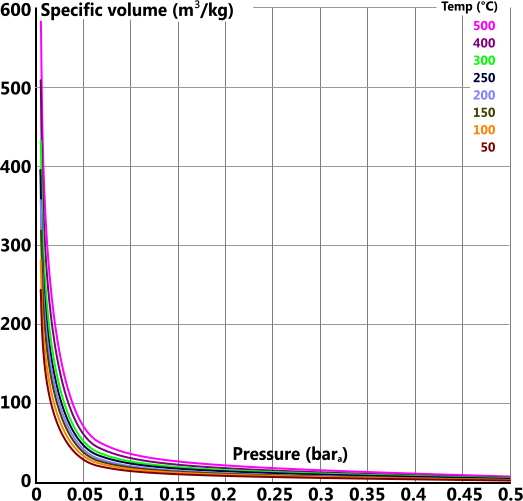
Specific Volume

Specific volume (v) is the volume 'per unit mass' of a substance

For reasons of clarity the specific volume graph has been split into four individual plots covering the total pressure range of 0bara 1000bara

Volume chart for superheated steam between 0 and 0.1bar

Fig 4a. Specific Volume 0bara to 0.5bara

Volume chart for superheated steam between 0.5 and 4bar

Fig 4b. Specific Volume 0.5bara to 5bara

Volume chart for superheated steam between 5 and 70bar

Fig 4c. Specific Volume 5bara to 70bara

Volume chart for superheated steam between 80 and 1000bar

Fig 4d. Specific Volume 70bara to 1000bara

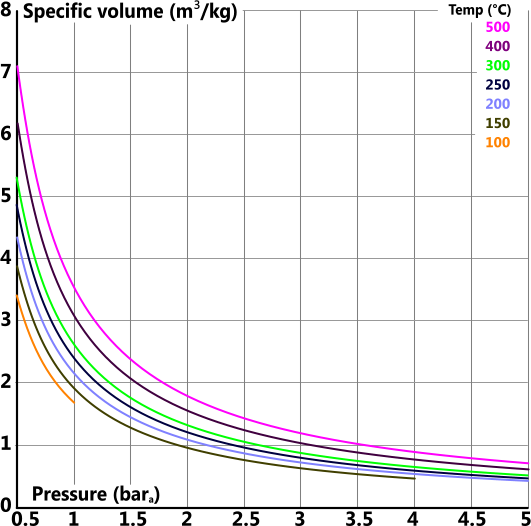
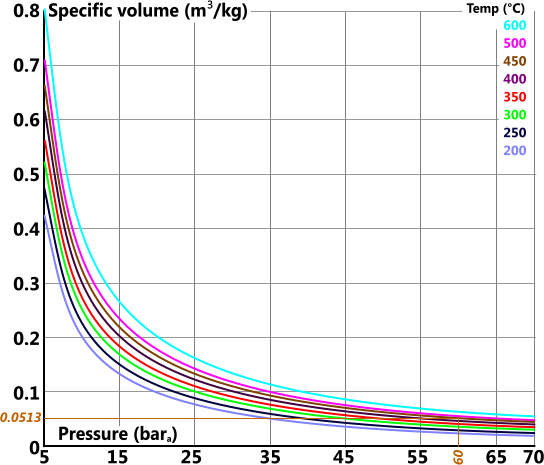
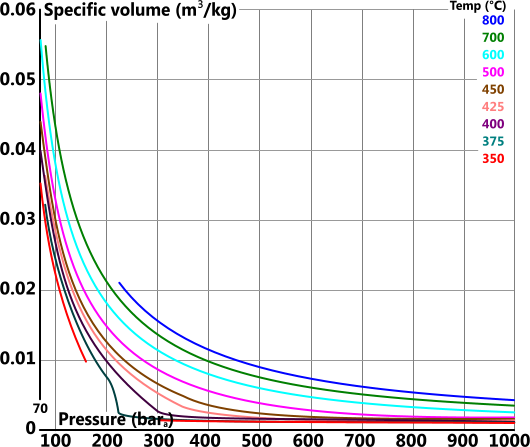
Specific Heat Capacity (constant pressure)

Specific heat capacity (cp) is the heat energy capacity 'per unit mass' of a substance

cp = cv + R

Fig 5. Specific Heat Capacity Chart for Superheated Steam

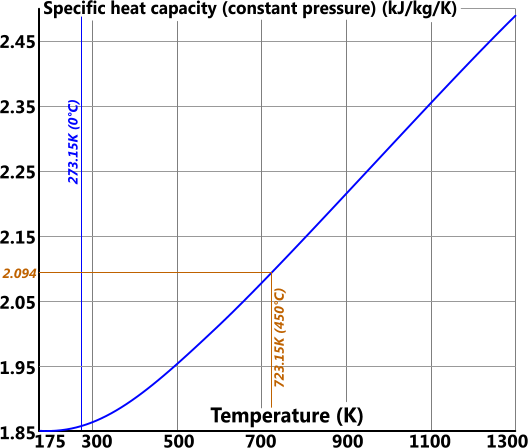
Additional Properties

From the above plots, it is possible to calculate other unknown properties of superheated steam at any designated pressure and temperature, such as:

Specific Gas Constant:
The universal gas constant (Rᵢ) that applies to all ideal gases describes the amount of energy available per mole of any gas for each degree of temperature above absolute zero (-273.15°C)
This can be modified to a gas constant for steam (Rₐ) as follows:
RAM H₂O = 18.01528 (Elements)
Rₐ = Rᵢ ÷ (RAM÷1000) = 8.314479 J/mol/K ÷ (18.01528 g/mol ÷ 1000)
Rₐ = 8.314479 J/mol/K ÷ 0.01801528 mol/kg = 461.523718 J/kg/K
Given that there are always the same number of molecules (N) in 1kg of a given substance irrespective of pressure, temperature and/or volume;
Rₐ must also be a constant (per kg) from; Rₐ = Rᵢ ÷ (RAM÷1000) = N.Rᵢ
where; N = number of moles

Specific Heats:
Specific heat capacity for 1kg of steam at 450°C and constant volume is calculated thus:
cp = 2094 J/kg/K (Fig 5)
cv = cp - Rₐ = 2094 J/kg/K - 461.523718 J/kg/K = 1632.476282 J/kg/K
and the ratio of specific heats (γ) is calculated as follows:
γ = cp / cv = 2094 J/kg/K ÷ 1632.476282 J/kg/K = 1.2827

PVn:
'n' in the formula 'P.Vn = R.T' for 1kg of steam at this temperature is calculated thus:
n = Log(V) / Log(R.T/P) = Log(0.053) ÷ Log(461.523718 x 723.15 ÷ 6,000,000) = 1.016733

Non-Specific Properties (mass ≠ 1kg)
for example; m = 2.5kg of steam
Gas Constant: R = m.Rₐ = 2.5 kg x 461.523718 J/K/kg = 1153.809294 J/K
Heat Capacity (constant pressure): Cp = m.cp = 2.5 kg x 2094 J/kg/K = 5235 J/K
Heat Capacity (constant volume): Cv = Cp - R = 5235 J/K - 1153.8093 J/K = 4081.1907 J/K
γ = Cp / Cv = 5235 J/kg/K ÷ 4081.1907 J/kg/K = 1.2827 (constant)
n = Log(V) / Log(R.T/P) = Log(0.053) ÷ Log(1153.8093 x 723.15 ÷ 6,000,000) = 1.489

The combination of 'R' (J/K) and 'n' will vary with the mass of water in the steam.

You will need to put 5235 Joules of energy into 2.5kg of water to achieve 60bara of pressure and 450°C, whereas you would only need to add 2094 Joules to achieve the same conditions for just 1kg of water.

Boiling Point of Water

The boiling point of any substance at a given pressure can be calculated using the following general formula:
Ṯ₁ = 1 ÷ [1÷Ṯ - Rᵢ x Ln(p₁÷p) ÷ Hv]
Where:
Ṯ is the boiling temperature at datum pressure (p) of the substance (e.g. 373.15K @ 1bar)
Ṯ₁ is the boiling temperature at modified pressure (p₁) of the substance
Rᵢ is the ideal gas constant (8.314478766579J/K/mol)
Hv is the latent heat of vaporisation of the substance at p (J/mol)
If you have a value for 'Hv' in J/g you must multiply the value by the RAM of the substance

This formula can be simplified as follows to cater for water on earth:
Ṯ₁ = 1 ÷ [0.00268 - 0.000204402 x Ln(p₁)]
Where:
Ṯ & Ṯ₁ are in K
p & p₁ are bar

Therefore, at 10bar: Ṯ₁ = 1 ÷ [0.00268 - 0.000204402 x Ln(10)] = 452.6K (179.5°C)

Notes

If measured accurately, the above graphs should be within 1.5%
For example the actual values for 60bara and 450°C are: 3301, 6.719, 2988, 0.0521 & 2.095 vs the readings from the above plots: 3302, 6.75, 2988, 0.0513 & 2.094