Magnetism
{© 02/12/24}Magnetism is the converse of electricity, it flows from positive to negative, it accrues between particles, and it is constant (irrespective of temperature).
Coulomb's Constant
Today, Coulomb's force constant has been manipulated in order to generate Newtons from Coulombs, and whilst his force formula is identical to Newton's and Gilbert's force formulas, Coulomb's constant does not have compatible units. As we understand it today, force is based upon kilograms (kg.m/s²), yet Coulomb's formula appears to generate this same force from electrical charge.
In order to rationalise Coulomb's constant 'k' with Newton's constant 'G', we must ensure that their units are identical. And to do this, we must incorporate electrical charge within his constant, such that we can use mass in his force formula.
The units for Newton's gravitational constant (G) have at last been finalised, along with its formula and its value; {m³ / kg.s²}
and using this constant, the potential force in a proton-electron pair at the neutronic state can be calculated like this;
Fₘ = G.ξₘ.(mₑ/Rₙ)²
Fₘ = 6.67359232004333E-11 x 1836.15115053207 x (9.1093897E-31 ÷ 2.81793795383896E-15)²
Fₘ = 1.28051247005732E-38 {kg.m/s²}
his potential energy at the neutronic state may be calculated like this;
PEₘ = Fₘ.Rₙ = 3.60840468973861E-53 {kg.m²/s²}
Coulomb's formula and units for 'k' are currently:
k = c².mₑ.Rₙ/e²
k = 8.98755184732666E+09 {kg.m³ / C².s²}
but because we are trying to calculate force (kg.m/s²), it should be; m³ / kg.s² as defined by Newton above.
We can correct it by incorporating the relative charge capacity (RC) and modifying his formula thus;
k' = k.RC² = e²/mₑ² . c².mₑ.Rₙ/e² = Rₙ.c²/mₑ
k' = 2.78024810626745E+32 {m³ / kg.s²}
Coulomb's potential force at the neutronic state becomes;
Fₑ = k'.mₑ²/Rₙ² = 2.78024810626745E+32 x (9.1093897E-31 ÷ 2.81793795383896E-15)²
Fₑ = 29.0535538991261 {kg.m/s²}
and his potential energy at the neutronic state becomes;
PEₑ = Fₑ.Rₙ = PEₙ = 8.18711122262533E-14 {kg.m²/s²}
the electrical charge is now included within Coulomb's constant.
The coupling ratio;
φ = Fₘ/Fₑ = PEₘ/PEₑ = 4.40742111792334E-40
Because magnetic charge forces accrue and electrical charge forces are shared; the coupling ratio becomes;
φ = (G.mₑ.mₚ/R²) / (k'.mₑ²/R²) = (G.ξₘ.mₑ²/R²) / (k'.mₑ²/R²) = G.ξₘ / k'
φ = 6.67359232004333E-11 x 1836.15115053207 ÷ 2.78024810626745E+32
φ = 4.40742111792334E-40
but now we are no longer trying to generate Newtons from Coulombs and the units of both constants are identical, what's more the coupling ratio becomes ...
φ = G.ξₘ / k' ...perfect
in which 'ξₘ' emphasises the converse between accrued magnetic charge force and shared electrical charge force.
Definitions
The traditional unit of measurement for "magnetic field strength" (B) is the Tesla. However, this is not a measurement of strength.
Strength refers to force, energy or power, whereas the Tesla refers to electrical charge per unit mass 'per second', which is neither force (kg.m/s²), energy (force times distance; kg.m²/s²) or power (energy per unit time; kg.m²/s³). Moreover, there is no time dependency on charge capacity.
Therefore, CalQlata has adopted the units for 'B' as kg/C, i.e. the reciprocal of relative charge capacity.
Convention today claims;
magnetic flux (Φ) is the equivalent of electrical current (I);
magneto-motive force (mmf) is the equivalent of electro-motive force (emf);
magnetic reluctance (R) is the equivalent of electrical resistance (R),
all of which relate either to energy (kinetic or potential); electrical and magnetic, so their units should reflect this relationship.
However;
Φ is measured in units of Weber (J.s/C)
mmf is measured in units of Ampere(-turns) (C/s)
reluctance = magneto-motive force ÷ magnetic flux; R = mmf/Φ
the units of which are; (C/s) ÷ (J.s/C) = C² / s².J
which is not the magnetic equivalent of electrical resistance; J.s/C²,
compare the units in this Table to understand this problem:
| magnetism | electricity | ||||
|---|---|---|---|---|---|
| label | symbol | units | label | symbol | units |
| flux | Φ | J.s/C | current | I | C/s |
| magneto-motive force | mmf | C/s | electro-motive force | emf | J/C |
| reluctance | R | C² / s².J | resistance | Ω or R | J.s/C² |
| Magnetic & Electrical Equivalents | |||||
When considered together with current belief that the constant 'B' represents a magnetic field, there is something amiss with our understanding of magnetism and the way we treat it, which also means that today's generally accepted definitions are incorrect.
The issue here is that the magnetic equivalent of the Coulomb is the kilogram, which is because we have not yet grasped the fact that mass is magnetic charge⁽¹⁾.
CalQlata has sorted this out in our calculations below, and in our definitions page.
Correction
We know that electricity is based upon the electrical charge of the electron, it is measured like this;
electro-motive force: V = Joules per Coulomb
this applies to the potential energy between a proton-electron pair.
It is this potential energy in an atom's outermost proton-electron pair(s) that must be exceeded if electrons are to be transmitted along a conductor. If the applied potential energy (Voltage) is greater than that required to extract the outermost electrons from their orbits, their transmission velocity will be greater than their extracted orbital velocity, increasing their orbital velocity when trapped by neighbouring protons. The resulting increased EME radiated by the pair will raise the orbital velocity of all the proton-electron pairs in all neighbouring atoms. This is the cause of rising temperature in a conductor with increasing applied Voltage.
current: I = Coulomb's per second
this can apply either to an orbiting electron within an atom (e.ƒ), or to the velocity of an electron once it has been extracted from its orbital shell due to an applied Voltage
The other properties are simply multiples of these two; resistance = V/I; power = V.I; etc.
In reality, magnetism is exactly the same, but it applies to the electron's magnetic charge, the magnitude of which is lower than electrical charge by the coupling ratio, so when electrical energy drives an electron, magnetism is simply a consequence. In electro-magnetism, however, both electricity and magnetism are of equal magnitude but opposite polarity, because the magnetic component is driven by electricity.
Magnetism should be measured like this (assuming we retain 'kilogram' as the unit for magnetic charge);
magneto-motive force: mmf = Joules per kilogram
this applies to the potential energy between a proton-electron pair.
flux: Φ = kilograms per second
We already know that magnetic charge is less than electrical charge by the coupling ratio (φ):
G.ξₘ.mₑ² / k.e² = φ
which gives us the following for the magnitude of the magnetic charge in an electron;
mₑ = √[ k.e².φ / G.ξₘ ] = 9.1093897E-31 kg
If, however, we recalculate k & G using unity for the values of all four primary constants at the neutronic condition: e=1; mₑ=1; Rₙ=1; tₙ=1; we get;
G = 9.47623573370968E-42 m³ / s².kg
because RC in this case is unity; e/mₑ = 1/1 = 1, k’s units are automatically corrected
k.RC² = k = 39.4784176043574 m³ / kg.s² (k = (2π)²)
G.ξₘ/k = φ
So now we can correct the above Table.
| magnetism | electricity | ||||
|---|---|---|---|---|---|
| label | symbol | units | label | symbol | units |
| flux | Φ | kg/s | current | I | C/s |
| magneto-motive force | mmf | J/kg | electro-motive force | emf | J/C |
| reluctance | R | J.s/kg² | resistance | Ω or R | J.s/C² |
| Corrected Magnetic & Electrical Equivalents | |||||
The corrected magnetic definitions are listed below:
Magnetic Charge: The non-polar magnetic charge in all atomic particles that we currently refer to as mass (kg),
Magnetic Constant: Joseph Henry's magnetic field generated by the proton-electron pair at its neutronic condition (kg.m/C²),
Magnetic Field: The general formula for Joseph Henry's magnetic field at any radial distance (kg.m/C²),
Magnetic Flux: Magnetic flow rate (kg/s),
Magneto-motive Force: Potential energy per unit magnetic charge {J/kg},
Permeability: The same as magnetic field (kg.m/C²),
Permeance: The reciprocal of reluctance (kg² / J.s),
Reluctance: The resistance to magneto-motive force (J.s/kg²),
that together, give us a genuine relationship (equivalence) between magnetism and electricity, along with a solid basis on which to resolve the issues with the definition and properties of magnetism.
Before reading further, it might be helpful to study our page on the basics.
Magnets

Fig 1. Bar Magnet
Permanent magnets, such as bar-magnets (Fig 1), are blocks of metallic elements that will generate a fixed magnetic field without outside help. Their magnetism cannot be switched on and off.
Electro-magnets (Fig 2), are coils of [generally] copper wire, that will generate a variable magnetic field whilst energised with an electrical current. Their magnetism can be switched on and off.
Bar magnets attract and repel by aligning their proton-electron pairs, and therefore, their magnetic fields, to act unidirectionally. A few elements are better at this than most.
Despite the statement below regarding temperature, the properties of any and all bar magnets can and will deteriorate with prolonged exposure to high temperature (and magnetic fields) simply due to changes in their lattice structures and crystallinity.
Some elements, such as; Neodymium, Cobalt, Gadolinium, Terbium, Dysprosium, etc., all of which are hcp, are naturally magnetic.
Iron, which is bcc, for example, can have its atoms aligned permanently if treated with a lodestone. But iron will lose its magnetic strength with time, if its atomic alignment is not periodically maintained.

Fig 2. Electro-Magnet
Electro-magnets generate magnetic fields simply by passing an electrical current along a conductor. The resultant magnetic field is naturally generated around the conductor normal to the electrical current; according to the right-hand rule. If the conductor is wound into a tight coil (adjacent wires are very close; Fig 2), it will act as a bar magnet (Fig 1), generating a magnetic field that will vary with the applied current.
A solenoid is a simple combination of the bar and electro magnets, the bar magnet being the central plunger and the coil acting as the surrounding energiser. The relative North-South pole positions will determine which direction the plunger is pushed; identical poles repel.
A transformer uses a non-magnetic iron core that will instantly magnetise when the surrounding coil is energised, and demagnetise the instant it is de-energised.
Magnetism in iron will become permanent if the coil remains energised for long periods which would render an iron core useless in AC transformers, in which its constant reversal (frequency) prevents the magnetisation from becoming permanent.
Calculations
The field of attraction between celestial bodies is due to the non-polar magnetic charge in their atomic particles (protons (mₚ), electrons (mₑ) and neutrons (mₙ)). It is what we today call gravity. This potential [gravitational] force is calculated as defined above;
Fₘ = G.mₑ.mₚ/R² {kg.m/s² = N}
Why does magnetism not vary with temperature?
The strength of attraction or repulsion in electro-magnets varies with temperature due to the electrical resistance in the energising coil, but it does not vary in bar-magnets; why?
Magnetic force at any distance (d) is calculated thus:
F = μ.I² . (2π)² = (mₑ.R/e²) x (e.ƒ.2π)² x (4π.R² / 4π.d²)
R is the electron orbital radius, and ƒ is the electron orbital frequency
remove the constants and we get:
factor = R.ƒ².R² = R³.ƒ² = 6.41524280848628 {m³/s²}⁽²⁾
which is the reciprocal of Isaac Newton's constant of proportionality for the proton-electron pair:
K = tₙ²/Rₙ³ = 0.15587874533403 s²/m³ = 1/factor
i.e. a constant!
irrespective of temperature.
... yet further vindication of the Newton-Coulomb atom, as if more was needed (Episode 52; Gravity & Episode 100; Verification).
Magnetic Fields
The term 'field' when used for magnetism and/or electricity refers to the remote attraction and/or repulsion between particles that are not in physical contact.
These filds can be static and dynamic.
Static Field
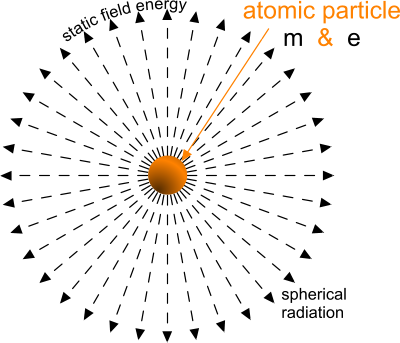
Fig 3. Static Field Energy
Atomic particles (protons and electrons) are packets of magnetic and electrical charge, both of which radiate constant fields of attraction and/or repulsion throughout the universe (Fig 3).
The static magnetic field radiated by all atomic particles attract (only) all other atomic particles in the universe, because magnetic charge is non-polar.
Whilst the magnitude of this field remains constant irrespective of environmental temperature (EME) and distance, it is distributed over the spherical area (4π.d²) at distance 'd', which is the reason the strength of attraction appears to diminish with the square of the distance (d²).
It is calculated in a proton-electron pair using Newton's force formula, thus;
Fₘ = G.mₚ.mₑ/R²
where; 'mₚ' is the magnetic charge (mass) of a proton, 'mₑ' is the magnetic charge of an electron, and 'R' is the electron's orbital radius.
Whereas the attraction force between collections of atomic particles (matter) is calculated like this;
Fₘ = G.m₁.m₂/d²
where; 'm₁' and 'm₂' are collections of atomic particles (masses), and 'd' is the distance between them,
but more accurately calculated like this;
Fₘ = G.(mₙ/d)² . (N₁.N₂)
where; 'mₙ' is the magnetic charge (mass; mₙ=mₚ+mₑ) of a proton-electron pair, and 'N₁' and 'N₂' are the numbers of proton-electron pairs in 'm₁' and 'm₂'; N = m/mₙ.
Note, because magnetic strength accrues, both 'm₁' and 'm₂' ('N₁' and 'N₂') can be any value.
The static electrical field radiated by all atomic particles repel (like poles) or attracts (unlike poles) all other atomic particles in the universe, because electrical charge is polar.
Whilst the magnitude of this field remains constant in electrons and lone protons, irrespective of environmental temperature (EME) and distance, it is distributed over the spherical area (4π.d²) at distance 'd', which is the reason the strength of attraction appears to diminish with the square of the distance (d²).
However, the magnitude of this field in proton partners (protons with an orbiting electron) varies with environmental temperature (EME) and distance, it is also distributed over the spherical area at distance 'd'.
It is calculated in a proton-electron pair using Coulomb's force formula, thus;
Fₑ = k.(e/R)²
where; 'e' is the electrical charge of an electron, and 'R' is its orbital radius.
However, because electrical charges are shared, the associated force between collections of electrons may be ignored as separation distances (R) are large;
Fₑ = k.(e/R)² . (Ň/N̂)
where; Ň is the lesser collection of electrons and N̂ is the greater collection.
For example:
The magnetic charge force (of attraction) between a proton-electron pair @ 300K is;
Fₘ = 2.96626261189654E-51 N
The electrical charge force (of attraction) between a proton-electron pair @ 300K is;
Fₑ = 6.73015473795743E-12 N
In this instance, the electrical force of attraction is 2.26890050495373E+39 times greater than the magnetic force of attraction.
Whereas the potential forces between two one-kilogram bodies one-metre apart (d), may be calculated like this;
The number (N) of proton-electon pairs in 1kg;
N = m/mₙ = 5.97538412973187E+26
where; mₙ is the mass of a proton-electron pair (1.67353257680E-27 kg)
Fₘ = 6.67359232004333E-11 N
Fₑ = 2.30707714465368E-28 N
In this instance, electrical force is 3.45702439408032E-18 times less than the magnetic force.
This discrepancy rises with increasing masses and separation distances, such as in celestial bodies.
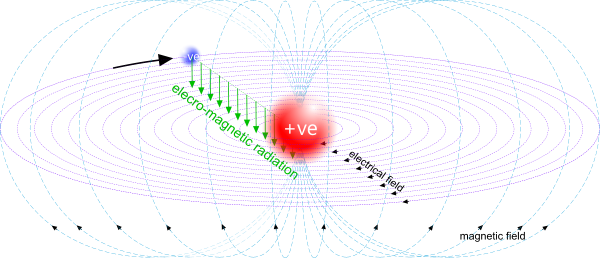
Dynamic Field
Dynamic fields are the electro-magnetic fields generated by proton-electron pairs (Fig 4); they are responsible for magnetic forces in bar magnets, solenoids and transformers.
Joseph Henry gave us a variable and a constant we can use today to define the strength of this field:
variable; μ = m.R/e² {kg.m/C²}
where; 'R' is the orbital radius of the proton-electron pair generating the field.
Bar Magnets
The strength of a bar magnet is due to the alignment of its shell-1 proton-electron pairs. In an iron magnet, this is achieved with a lodestone.
Therefore, the strength calculated below is a maximum value that is dependent upon the care with which the lodestone is applied.
For example;
The electro-magnetic force generated by a single proton-electron pair @ 300K may be calculated like this;
Fₘ = μ.I² . (2π)² = 1.23575813653594E-08 N
where; μ = mₚ.R₁/e²; I = (e.ƒ₁); R₁ = Xᴿ/Ṯ; ƒ₁ = (Ṯ/Ṯₙ)¹˙⁵ / tₙ
The electro-magnetic force generated by an iron bar magnet of 0.1 kilogram at a distance of 'd=0.25' metres may be calculated like this;
distance 'd' is between centres of mass
the number of shell-1 proton-electron pairs in this bar magnet is; N° = 2.Z/RAM . m/mₐ = 9.96252618319693E+23
every iron atom has two shell-1 proton-electron pairs
Fₘ = N° . μ.I² . (2π)² . (R₁/d)² = 6.75242865803415 N
If you position two identical bar magnets (as described above), the attraction force between their opposite poles will be twice the above value.
If you position two identical bar magnets (as described above), the repulsion force between their identical poles will be twice the above value.
Solenoid
The conventional calculation method is;
where; N is the number of turns and A is the coil cross-sectional area
Fₘ = μ.(N.I)².A / 2.d²
actually, 'A' & 'N' play no part in this formula, what's important is the length of wire involved (ℓ).
So, if we rewrite the formula on this basis;
Fₘ = μₒ.I² . ½.(ℓ/d)²
For example: I = 1 Amp; ℓ = 100m; d = 0.01m;
Fₘ = 5 N
but the problem with this formula, is that it takes no account of temperature.
Whilst magnetism does not vary with temperature (theoretically), this is not the case with electro-magnetism, because electrical resistance does. For any given current, if resistance increases, Voltage (J/C) falls, and the Joules per Coulomb are responsible for the applied force.
Electro-magnetic field strengths (electrical and magnetic) are equal (and opposite). That is why we can calculate it using Coulomb's force formula;
F = k'.mq²/R₁² = k.(I/ƒ₁)²/R₁²
alternatively, we could use Henry's formula;
F = μ₁.I² . (2π)²
because all of these formulas give identical results.
All of the following properties of the shell-1 proton-electron pairs will vary with temperature,
for example; @ 300 K;
R₁ = Xᴿ/Ṯ = 5.85488721693444E-09 m
mq = I/ƒ₁ / RC = 1.00565768978436E-24 kg
ƒ₁ = (Ṯ/Ṯₙ)¹˙⁵ / tₙ = 5.65364778201147E+12 /s
μ₁ = mₑ.R₁/e² = 0.20777204157239 kg.m/C²
the force generated, according to Coulomb and Henry, is as follows;
F = 8.20251142370473 N
whereas @ 273.15K;
F = 9.00879892773721 N
Coils & Transformers
The same rules apply to any use of coils in electro-magnetism
The number of turns and the coil cross-sectional area play no part in the holding force of a solenoid's plunger, and the current alone is responsible for its dynamic force (mass x acceleration):
1) you need at least one loop to induce a magnetic force in a plunger (or core),
2) wire 'length' and applied 'current' are the only factors that define the holding force in a plunger,
3) dynamic force in a plunger through a loop is defined by current alone.
In a transformer, it doesn't matter how many coils you wrap around the core, the conversion between voltage and current will always be correct if the [wire length] ratios are correct.
Notes
- If we fully understood the concepts of electricity and magnetism, both of which comprise charge and field, and together their charges generate EME, we would realise that the units of measurement for their respective forces and their equivalence should be as follows:
magnetic force (accrues): Fₘ = G.m₁.m₂/R² {kg.m/s²}
electrical force (shared): Fₑ = k.e²/R² {C.m/s²}
equivalence Fₘ:Fₑ = Fₘ/Fₑ = φ (the coupling ratio). - When the reciprocal of this factor (1/K) is divided by the mass of an electron, we get Coulomb's modified constant; k' = 4π² / K.mₑ = 2.78024810626745E+32 {m³/s² / kg}.
- The highest energy electron shells will dominate the reaction in magnetism and lodestone alignment. This means that shell-1 proton-electron pairs will define magnetic strength, and every atom (except hydrogen) must have at least two aligned electron shells, because two proton-electron pairs always occupy shell-1.
- Lodestones are not the only method of creating permanent magnetism in a bar-magnet, you can also put it inside an energised electro-magnetic coil. But the thicker the bar, the more time and current (in the electro-magnetic coil) will be required to maximise its strength.
Further Reading
You will find further reading on this subject in reference publications(3, 68, 69, & 70)