Magnetism; the Basics
The profusion of constants, variables and formulas we have generated over the years, together with our confusion over the units of measurements, make it abundantly clear that we do not understand magnetism.
Yet it isn't as complicated as it appears. Electrical and magnetic charges are straightforward enough; there's nothing mystical or complicated here. If you revolve one of these charges about the other, you will generate electrical and magnetic fields, the magnitude of which is based upon the performance of the proton-electron pair, and that's it; simple isn't it.
But before we can measure magnetism, we must understand it, both logically and mathematically, and to understand it, we need to know its origins.
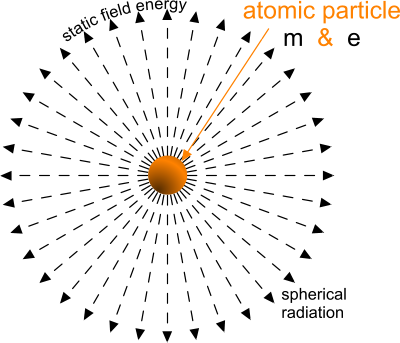
Fig 1. Static Field Energy
Universal Matter
Statements of fact:
Everything in the universe comprises only electrons and protons, that exist as; neutrons, proton-electrons pairs or lone electrons and lone protons; nothing else.
Every lone electron is identical to every other lone electron, and every lone proton is identical to every other lone proton.
Every electron and every proton is a packet of electrical and magnetic charge; nothing else.
Electrons and protons are indivisible; they do not comprise smaller particles.
The electrical charges of both lone particles are of equal magnitude that radiate static electrical fields of attraction or repulsion (Fig 1) according to their polarity; the electron being negative and the proton being positive.
The magnetic charges of both particles, which are of unequal magnitude, radiate static magnetic fields of attraction (Fig 1) according to their magnitude.
The magnitude of the proton's magnetic charge is greater than that of the electron by the static ratio 'ξₘ', and both magnitudes are constant.
The static magnetic field radiated by both particles are of attraction only, because their magnetic charges are non-polar.
When united as a proton-electron pair, the orbiting electron will collect energy from its surrounding EME and;
a) alter its kinetic energy accordingly, and;
b) transfer electrical energy to its proton partner, which - using its additional magnetic charge - the proton will convert to, and augment, its own electrical charge commensurate with the magnitude of the EME collected, and;
c) the pair will radiate EME of the same magnitude as the EME collected, and;
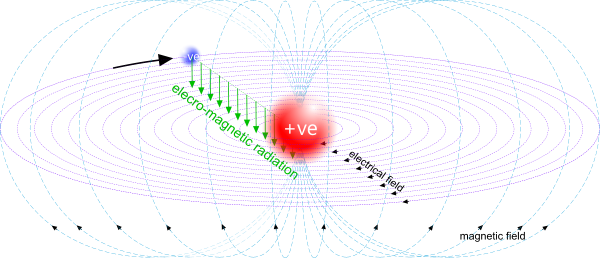
d) generate dynamic electrical and magnetic fields (Fig 3).
Atomic Particles
The electron is a packet of e Coulombs of electrical charge, and mₑ kilograms of magnetic charge, both of which are constant.
The proton is a packet of e Coulombs of electrical charge, and mₚ kilograms of magnetic charge, both of which are constant whilst the proton remains alone.
When the proton traps an electron partner, its electrical charge will vary between e > e' > eₙ
where; eₙ = mₚ.RC
The additional electrical charge in a proton (e') cannot affect the potential energy in a proton-electron pair as their shared energy must be the lesser of the two, that of the electron; e;
The purpose of this additional proton electrical charge (e') is to repel adjacent atoms, causing the matter to exist in a gaseous or viscous state.

Fig 2. Dynamic Field Energy
Magnetic and Electrical Charges
Mass and inertia (kilograms) are the terms (and unit) we use today for non-polar magnetic charge. And gravity is the attractive static field energy (Fig 1) radiated by this magnetic charge.
Polar electrical charges (Coulombs) also radiate a static field energy, but the attraction or repulsion between adjacent atomic particles is dependent upon their relative polarity (positive and/or negative).
This static field energy is calculated using Newton's (magnetic) and Coulomb's (electrical) energy formulas;
E = G.m₁,m₂/R and E = k.e²/R respectively
where 'm₁' and 'm₂' are magnetic charges, and 'e' is electrical charge.
Static Fields
Whilst these static fields are radiated at constant magnitude throughout the universe, irrespective of distance (Fig 1), they are distributed over the spherical area (A = 4π.d²) at any distance 'd', so they will appear to diminish with distance between any two particles.
Whilst the dynamic fields generated by proton-electrons pairs are stronger than the static fields by the coupling ratio, their field of influence is highly localised (Fig 2).
Static Field Energy
Because magnetism accrues ...
... the accumulation of protons, electrons and neutrons will result in an increase of this energy, exactly as Newton and Gilbert predicted, where m₁ and m₂ are collections of magnetically charged particles.
As you can imagine, the magnetic field between particles will be tiny until their number becomes huge, e.g. in celestial bodies.
For example; the potential energy of attraction between two protons 1E-09m apart will be;
E = G.mₚ²/d = 1.86704632674428E-55 Joules.
Whereas accretion means that the same energy between the earth, which contains 3.5600520242213E+51 (N₂) proton-electron pairs, and our sun, which contains 1.18820513419718E+57 (N₁) proton-electron pairs, at the earth's orbital perigee will be;
E = G.mₚ²/d . N₁.N₂ = 5.37499262449805E+33 Joules.
N₁ & N₂ include neutrons because neutrons have the same magnetic charge (mass) as a proton-electron pair
Because electricity is shared ...
... the accumulation of protons and electrons will result in a decrease of this energy, exactly as Coulomb predicted; where e is the lesser magnitude of any two interacting electrically charged particles. As you can imagine, the electrical field between particles will decrease as the number of adjacent particles increases; becoming negligible between atomic particles in celestial bodies.
For example; the potential energy of repulsion between two protons 1E-09m apart will be;
E = k.e²/d = 2.30707714465368E-19 Joules.
Whereas sharing means that the same energy between any two protons in the earth will be;
E = k.e²/d / N° <≈ 2.03549762377506E-86 Joules
where 'd' is approximated to half earth's radius
N° excludes neutrons, because neutrons do not radiate electrical charge
As you can see; the electrical repulsion between two adjacent protons is 1.23568285993027E+36 times greater than their magnetic attraction, proving that our solar-system cannot possibly have accreted from hydrogen gas.
Moreover, the electrical interaction between the earth's atomic particles shows us why there is negligible electrical interaction between celestial bodies.
Summary
Every atomic particle possesses magnetic and electrical charge that radiates a static field energy throughout the universe, and interracts with every other atomic particle in the universe.
Magnetic static field energy accrues between atomic particles, increasing with their accumulation in a collective body.
Electrical static field energy is shared, between atomic particles, decreasing with their accumulation in a collective body.
Whilst the strength of this energy remains constant throughout the universe, it is distributed over the spherical area at the radial distance from its origin.
The strength of these fields are calculated according to Newton's and Coulomb's force formulas.
This is an accurate and straightforward calculation for the magnetic strength (potential and gravitational) between every body in the universe; atomic and celestial (e.g. Newton's laws of orbital motion).
Magnetic and Electrical Fields
First we must validate Joseph Henry's magnetic field force formula by comparing it to force formulas we already know.
The controlling constants:
hₑ = Rₙ.c = 8.4479654849081E-07 m²/s Newton's constant of motion for the orbiting electron at the neutronic condition
μₒ = mₑ.Rₙ/e² = 1.00000000000000E-07 kg.m / C²
c = 2πRₙ/tₙ = 2.99792459E+08 m/s
I = e.ƒ = e/t
Fₘ = μ.I² . (2π)² kg.m/s²
e.ƒ is the current generated by an orbiting electron in a proton-electron pair
The standard force formulas:
F = μₒ.(e/tₙ)² . (2π)² = 29.0535538991261 kg.m/s²
F = k'.(mₑ/Rₙ)² = 29.0535538991261 kg.m/s²
F = k.(e/Rₙ)²= 29.0535538991261 kg.m/s²
F = G/φ . ξₘ.(mₑ/Rₙ)²= 29.0535538991261 kg.m/s²
all of which give identical results to that of the neutronic force in a proton-electron pair;
Fₙ = PEₙ/Rₙ = mₑ.c²/Rₙ = 29.0535538991261 kg.m/s²
Now if we generate a force factor (F) using Henry's formula:
F = μ.I² . (2π)² . R³ kg.m⁴/s²
and apply it to the proton-electron pair in the neutronic Condition;
F = μₒ.(e/tₙ)² . (2π)² . Rₙ³ = 6.50120024835403E-43 kg.m⁴/s²
F = mₑ.Rₙ/e² . e²/tₙ² . (2π)² . Rₙ³
F = mₑ.Rₙ⁴ / tₙ² . (2π)²
F = mₑ.Rₙ⁴ . (2π/tₙ)²
F = mₑ.Rₙ² . (2πRₙ/tₙ)²
F = mₑ.Rₙ² . c²
F = mₑ . (Rₙ.c)²
F = hₑ².mₑ = 6.50120024835404E-43 kg.m⁴/s²
This means that Joseph Henry's force formula is directly related to Newton's constant of motion in a proton-electron pair.
Moreover, when we divide this value by volume (Rₙ³), we get Fₙ;
Fₘ = hₑ².mₑ/Rₙ³ = 29.0535538991261 kg.m/s²
This procedure has demonstrated that all of the formulas are; a) related, and ; b) correct. So, it shouldn't be too difficult to derive a magnetic field force from Henry's formula.
Calculations
Electro-Magnetic field strength must be measured in units of force; kg.m/s², which may be achieved from Henry's formula;
μ = m.R/e² {kg.m/C²}
along with internal (atomic) current;
I = e.ƒ {C/s}
where; ƒ = (Ṯ/Ṯₙ)¹˙⁵ / tₙ
F = μ.I² . (2π)² {kg.m/C² . (C/s)² = kg.m/s²}
The magnetic field strength of a proton-electron pair may be calculated as follows:
μ = mₑ.R/e² {kg.m/C²}
where; R = the electron orbital radius.
Fₚₑₚ = μ.(e.ƒ)² . (2π)²
Fₚₑₚ = mₑ.R/e² . (e.ƒ)² . (2π)² {kg.m/s²}
Fₚₑₚ = mₑ.R.ƒ² . (2π)² {kg.m/s²}
@ 300 K:
μ = 0.20777204157239 kg.m/C²
Fₚₑₚ = 6.73015473795743E-12 {N}.
But both magnetic charges (the proton and the electron) contribute to the electro-magnetic field energy generated by a proton-electron pair, so we must multiply this result by the static ratio; ξₘ;
F = 1.23575813653594E-08 N
The electrical field strength of a proton-electron pair may be calculated as follows:
k = mₑ.Rₙ³/e² . (2π/tₙ)² {kg.m³ / s².C²}
Fₚₑₚ = k.(e/R)²
where; R = the electron orbital radius.
Fₚₑₚ = k'.(mq/R)² {kg.m/s²}
where; mq = e/RC
@ 300 K:
Fₚₑₚ = 6.73015473795743E-12 {N}
But both magnetic charges (the proton and the electron) contribute to the electro-magnetic field energy generated by a proton-electron pair, so we must multiply this result by the static ratio; ξₘ;
F = 1.23575813653594E-08 N
As you can see, the electrical and magnetic potential forces (Fₚₑₚ) in a proton-electron pair are identical. But as they accumulate, interracting magnetic forces between atomic particles will accrue (increase), and interracting electrical forces are shared between atomic particles (decrease). This is why two planets are magnetically attracted, but electrical interraction is non-existant.
Because these forces are identical in a proton-electron pair, their electro-magnetic field forces will also be identical, but the rules for magnetic accrual and electrical sharing still apply.
Bar Magnets
Bar magnets radiate (Fig 2) dynamic field forces (Fig 3) in their aligned shell-1 proton-electron pairs in their atomic elements.
The field forces generated by a proton-electron pair @ 300K are calculated as follows:
magnetic: Fₘ = mₚ.R₁.ƒ₁² . (2π)² = 1.23575813653594E-08 N
electrical: Fₑ = kꞌ.⁺mₚ.⁻mₑ/R₁² = -1.23575813653594E-08 N
Excluding neutrons because they do not generate the fields we are seeking.
Now we can apply these field forces (magnetic and electrical) to an iron bar magnet @ 300 K thus:
material properties (iron):
atomic mass; mₐ = 9.34617738165495E-26 kg;
bar mass; m = 0.1 kg;
distance between centres of mass; d = 0.25 m
number of shell-1 proton-electron pairs: N° = 2.Z/RAM . m/mₐ = 9.96252618319694E+23
every atom (except hydrogen) has two shell-1 proton-electron pairs
magnetic (accrued): Fₘ = mₚ.R₁.ƒ₁² . (2π)² . N° . (R₁/d)² = 6.75242865803416 N
electrical (shared): Fₑ = k.(e/d)² / N° = -3.7052082610049E-51 N
Note: this value does not vary with temperature as the use of R₁ and ƒ₁ cancel out. Confirming that Henry's field formula complies with the known fact that intrinsic (non-electrical) magnetism does not vary with temperature.
This exercise demonstrates the reduction of electrical field force with the accumulation of atomic particles.
If you position two identical bar magnets (as described above), the attraction force between their opposite poles will be twice the above value.
If you position two identical bar magnets (as described above), the repulsion force between their identical poles will be twice the above value.
Solenoid
The force induced by a solenoid plunger on its target, separated by distance 'd' (Fig 4), may be calculated as follows:
This force is due to solenoid activation; the applied current.

Fig 4. Solenoid Force
The conventional calculation method is;
where; N is the number of turns and A is the coil cross-sectional area
F = μ.(N.I)².A / 2.d²
actually, 'A' & 'N' play no part in this formula, what's important is the length of wire involved (ℓ).
So, if we rewrite the formula on this basis;
F = μ.I² . (ℓ/d)² / 8π
and,
F = μₒ.I² . ½.(ℓ/d)²
we get exactly the same result but the calculation is much simpler.
Therefore, the best version of this formula must be:
F = μₒ.I² . ½.(ℓ/d)²
For example: I = 1 Amp; ℓ = 100m; d = 0.01m;
F = 5 N
but the problem with this formula, is that it takes no account of temperature.
Whilst magnetism does not vary with temperature (theoretically), this is not the case with electro-magnetism, because electrical resistance does. For any given current, if resistance increases, Voltage (J/C) falls, and the Joules per Coulomb are responsible for the applied force.
Because of magnetic accrual and equal electrical and magnetic forces in a proton-electron pair, we can use both Coulomb's and Henry's force formulas to determine the strength of a solenoid;
F = k'.mq²/R₁² = k.(I/ƒ)²/R₁² = μ₁.I² . (2π)²
all of which give identical results.
The following properties of the shell-1 proton-electron pairs will vary with temperature,
for example; @ 300 K;
R₁ = Xᴿ/Ṯ = 5.85488721693444E-09 m
mq = I/ƒ / RC = 1.00565768978436E-24 kg
ƒ = (Ṯ/Ṯₙ)¹˙⁵ / tₙ = 5.65364778201147E+12 /s
μ₁ = mₑ.R₁/e = 0.20777204157239 kg.m/C²
the force generated, according to Coulomb and Henry, is as follows;
F = 8.20251142370473 N
whereas @ 273.15K;
F = 9.00879892773721 N
Realisation that the number of turns and the coil cross-sectional area play no part in the holding force of a solenoid's plunger, and that current alone is responsible for its dynamic force (mass x acceleration), we can conclude the following:
1) we need at least one loop to induce a magnetic force in a plunger (or core),
2) wire 'length' and applied 'current' are the only factors that define the holding force in a plunger,
3) dynamic force in a plunger through a loop is defined by current alone.
In a transformer, for example, it doesn't matter how many coils you wrap around the core, the conversion between voltage and current will always be correct if the [wire length] ratios are correct.
input and output power (current x Voltage) will always be identical (minus losses).
The length and diameter of the wire used in a transformer's coils are important factors in minimising its losses;
1) the smaller the wire diameter, the greater its temperature, and the greater its electrical resistance,
2) the longer the wire, the greater its electrical resistance,
in either/both cases, transformer efficiency will be reduced.
In other words, both of the following example transformers ...
1) 0.5mm diameter wire, input circuit 300 turns, output circuit 200 turns
2) 20mm diameter wire, input circuit 3 turns, output circuit 2 turns
... will result in the same electrical conversion, but losses in example 2) will be lower; greater efficiency.
Finally
Today, we define both electrical and magnetic force (kg.m/s²) using magnetic charge (kilogram), whereas electrical charge forces should be based upon electrical charge (Coulombs).
This confusion has arisen because we have not yet realised that mass is actually magnetic charge, which has led to our having given the elementary magnetic charge (mₑ) and the elementary electrical charge (e) different magnitudes, whereas they are actually equal.
To overcome this problem, Coulomb found it necessary to convert electrical charge to mass in his constant (k), and we need a relative charge capacity constant (RC) to compensate for this misconception.
In reality, we would all find mathematical physics infinitely simpler if we set the four basic constants (distance, time, magnetic and electrical charges) to unity at the neutronic condition, and accepted a common formula for both magnetism and electricity, whereupon the Newton's and Coulomb's force constants would have corrected magnitudes, that reflect the coupling ratio, and compatible units;
aₒ = (ξᵥ / 4π)² = 18778.8808461551 m
c = 2π = 6.28318530717959 m/s
mᵤ = 1 / (⁴/₃π.rₑ³) = 7.82336489952175E+46 kg
G = aₒ.c/mᵤ = 9.47623573370968E-42 m³ / kg.s²
μ₀ = Rₙ.mₑ/e² = 1 kg.m/C²
k = (2π)².μ₀ = (2π)² = 39.4784176043574 m³ / C.s²
The magnetic force in a proton-electron pair becomes;
Fₘ = G.ξₘ.(mₑ/R)² kg.m/s²
The electrical force in a proton-electron pair becomes;
Fₑ = k.(e/R)² C.m/s²
And the coupling ratio becomes;
φ = Fₘ/Fₑ = G.ξₘ/k = 4.40742111792334E-40 kg/C
because; mₑ=1 kg and e=1 C