Thermodynamics
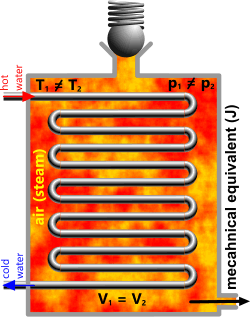
Fig 1. Constant Volume⁽¹⁾
The term ‘thermo’ implies heat; and the term ‘dynamic’ implies movement. So ‘thermodynamic’ means the movement of ‘heat’. And because heat is EME, thermodynamics is nothing more than the transfer (or movement) of EME.
It is important to remember the first two laws of thermodynamics;
1) Energy is never lost or gained from a process. All the energy present (in the system) at the start of a process, plus that which is added (or subtracted), is still there at the end of the process; it is simply redistributed.
2) You can’t increase the energy in a system by taking energy out of it (removing heat).
Validity of the third law is questionable because ‘entropy’ is ambiguous; open to interpretation.
Systems & Processes
The complicated bit is deciding on the most appropriate process of energy transfer within a system, for example:
The transfer of energy through a tube inside a pressure vessel (heat exchanger) is generally considered to be ‘constant volume’; also referred to as isochoric.
The transfer of energy onto a piston inside a cylinder (internal combustion engine) is generally considered to be ‘constant pressure’; also referred to as isobaric.
The transfer of energy inside a hot-air balloon of ‘constant temperature’, the volume and pressure of which is free to vary with altitude; also referred to as isothermal.
The transfer of energy inside a system in which the energy is constant, but in which pressure, temperature and/or volume may vary individually, is generally considered to be ‘adiabatic’; also referred to as isentropic.
The transfer of energy in which any or all of the above may occur is generally considered to be an ‘absolute’ process; also referred to as polytropic.
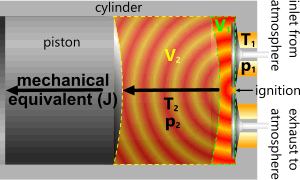
Fig 2. Constant Pressure⁽¹⁾
However, most processes are polytropic, and also prone to energy loss into the environment, so, unless the exact ‘before’ and ‘after’ conditions are fixed and known, it is important to ensure that all aspects of the process and the system, including the environment, are carefully considered in thermodynamic calculations.
For example, whilst the conditions within a cylinder may be reliably replicated theoretically, process losses can come from any part of the system; heat losses through the cylinder-wall; temporary air pressure build-up behind the piston; pressure loss across piston rings; etc. It is up to you to determine the need for their inclusion in your calculations.
The gas or liquid medium responsible for transfer of energy is referred to here as the 'medium'.
Gas Constant (R)
The principal input constant for thermodynamic calculations is the gas constant - which applies to both viscous and gaseous matter - and it comes in three forms:
Rᵢ = {J/K/mol, ft-lbf/R/mol, etc.}
Rₐ = Rᵢ/RAM {J/K/kg, ft-lbf/R/lb, etc.}
R = Rₐ.mass {J/K, ft-lbf/R, etc.}
In your own hand calculations, if you're looking for results per unit mole; e.g. J/K/mol, ft-lbf/R/mol, etc., you must use Rᵢ and mass = 1/RAM#. This option doesn't apply to Thermodynamics calculations, which only uses Rₐ.
Rₐ is used only for isothermal calculations in Thermodynamics.
Your output units will depend upon the value entered for 'mass', for example;
if you want specific results (per unit mass), you must enter 'm' = 1; and your results will be both specific {J/K/kg or ft-lbf/R/lb}, and actual {J/K or ft-lbf/R}. But don't forget; your volumes must also be specific {m³/kg or ft³/lb};
if you enter something other than '1' for 'm', your result will be actual (for the mass entered) {J/K or ft-lbf/R}.
# Don't forget to convert RAM to the correct units; e.g. RAM for N₂ is 14.0067, which is also g/mol, so, to convert this to kg you must divide the RAM by 1000 (RAM ÷ 1000), or to lb you must multiply RAM by 0.00220462 (RAM x 0.00220462). The correct gas constant will then be; Rᵢ divided by the converted value for RAM, which is Rₐ.
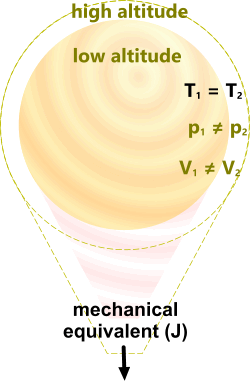
Fig 3. Constant Temperature⁽¹⁾
Specific Heat Capacities (cₚ, cᵥ) & their Ratio (γ)
The specific heat capacity (SHC) of any atom describes the amount of kinetic energy in its orbiting electrons per unit mass per unit temperature any atom can hold, and is not temperature dependent.
In other words, it is a measure of the EME intensity radiated by all of the proton-electron pairs in a unit mass of the matter for each degree of temperature change, and it is consistent and constant.
It is described as follows:
Constant Pressure: cₚ = SHC
Constant Volume: cᵥ = cₚ/γ
Absolute: cₙ = cᵥ.(n-γ)/(n-1)
The specific heat ratio (γ) ranges between; >1.0 for the most complex molecules to 1⅔ for monatomic atoms.
The ratio of specific heats for diatomic gases is 1.342, and because 99% of our atmosphere comprises diatomic gases (N₂ & O₂), this is the value you may use in your calculations for air.
If you wish to calculate the specific heat capacity of a compound gas, you may do so as follows:
if 'm' represents the total mass of the gas or matter,
'm₁' represents the mass of element-1 in 'm' and SHC₁ represents its specific heat capacity,
'm₂' represents the mass of element-2 in 'm' and SHC₂ represents its specific heat capacity,
'm₃' represents the mass of element-3 in 'm' and SHC₃ represents its specific heat capacity,
etc.
the effective specific heat capacity of the total mass: SHC = SHC₁.m₁/m + SHC₂.m₂/m + SHC₃.m₃/m + etc.
Exponent (n)

Fig 4. Adiabatic⁽¹⁾
The exponent that applies to your input variables depends upon your operating system:
Constant Volume: n = ∞;
Constant Pressure: n = 0;
Constant Temperature: n = 1;
Adiabatic: n = γ;
Absolute: n = ln(p₁/p₂) / ln(V₂/V₁)
PVRT
The formula p.V=n.Rᵢ.Ṯ is generally used to calculate the properties of a gas, based upon the ideal gas constant and number of moles of matter in the gas under consideration.
This calculation is provided in Thermodynamics under the 'Constants' calculation option, the results for which are provided with the output symbol; 'pᵣ'. This value will be correct irrespective of the units used for your input data, as long as they are consistent.
But there is now an alternative calculation technique based upon the kinetic energy of an atom's innermost proton-electron pairs, that provides identical results; 'pₑ'. This calculation option is provided only for those wishing to verify the Newton-Coulomb atom.
However, this calculation uses hard-wired values for the mass of a neutron and relies on knowing the number of proton-electron pairs and neutrons in the gas atoms (or molecules) to calculate its atomic (or molecular) mass; mass = RAM (g/mol) x mₙ, therefore, this output value only works if the input data is entered in kilograms.
Input & Output Variables
All thermodynamic calculations begin with a process start, which is identified with the subscript '1', and a process end, which is identified with the subscript '2'.
Your primary input variables are for the variations in pressure, temperature and volume, at the start of the process and at the end of it.
You will also need to enter specific heat values for the gas (or matter) concerned, along with its mass.
But because of the various relationships for each system/process, it is possible to predict one of the input variables in each case. Therefore, if there are six possible inputs, you only need to enter values for five, the remaining value can be calculated automatically.
Your primary output variables are the amounts of heat (Q) and work (W) transferred during the process, together with the changes in internal energy (δU), enthalpy (δH) and entropy (δS).
The work done (W), is equal to the equivalent mechanical energy, after subtracting any losses in the system.
System Constants and Performance Relationships
The following relationships and constants identify each potential system/process; you must select your own calculation option and input data that best suits your own.
Constant Volume
V is a constant
V₂/V₁ = Ṯ₂/Ṯ₁
Constant Pressure
p is a constant
p₂/p₁ = Ṯ₂/Ṯ₁
Constant Temperature
Ṯ is a constant
p₂/p₁ = V₁/V₂
Adiabatic
p.Vγ is a constant
p₁.V₁γ = p₂.V₂γ
and;
p₁.V₁/Ṯ₁ = p₂.V₂/Ṯ₂ (two or more properties of which may vary)
Absolute
p.Vⁿ is a constant
p₁.V₁ⁿ = p₂.V₂ⁿ
Thermodynamics Calculator - Technical Help
Thermodynamics calculates the energy used or expended during a process that involves a change in the temperature, volume and/or pressure of a medium.
Units
You may use any units you like in these calculations, but you must be consistent. Metric and Imperial values and/or conversions are provided in the Technical Help menu for gas constants and specific heat capacities.
Calculation Procedure
Apart from the 'Constants' calculation option, there are six possible input values; p₁, V₁, Ṯ₁, p₂, V₂ & Ṯ₂. Thermodynamics will expect you to provide five or six of these (dependent upon the calculation option), and the missing value will be calculated automatically.
You must delete the value(s) you wish the calculator to calculate for you.
Thermodynamics will provide messages (at the top of the calculator window) to guide you towards a successful calculation, after which the messages will be replaced by a CalQlata logo image.
For reasons of clarity; if you see the CalQlata logo at the top of the calculator (Fig 5), the calculation has been successful, otherwise, you will need to incorporate the changes recommended by the message presented.
You will then be provided with the energies expended during the process; Q, W, δU, δH & δS.
If you divide the energy by time, you will have the power (J/s or W) available from the process.
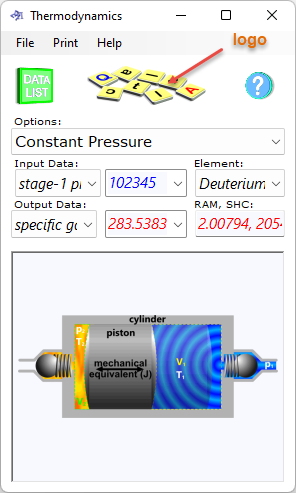
Fig 5. Successful Calculation
Input Data
Constants
Rᵢ; ideal gas constant.
cᵥ; specific heat capacity of the medium for constant volume.
cₚ; specific heat capacity of the medium for constant pressure.
RAM; relative atomic mass of the medium.
m; the mass of the medium.
Ṯ; gas temperature; applies to pᵣ and pₑ calculations only.
ρ; gas density; applies to pᵣ and pₑ calculations only.
Constant Volume; Constant Pressure; Constant Temperature; Adiabatic; Absolute;
p₁; the pressure in the medium at the start of the process (stage 1)
V₁; the volume of the medium at the start of the process (stage 1)
Ṯ₁; the temperature of the medium at the start of the process (stage 1)
p₂; the pressure in the medium at the end of the process (stage 2)
V₂; the volume of the medium at the end of the process (stage 2)
Ṯ₂; the temperature of the medium at the end of the process (stage 2)
Output Data
Rₐ; gas constant (per unit mass).
R; gas constant for the total mass of the medium.
pᵣ; classic pressure of gas density (ρ) and temperature (Ṯ); see PVRT above.
pₑ; Newtonian pressure of gas density (ρ) and temperature (Ṯ); see PVRT above.
γ; specific heat ratio of the medium.
n; exponent for the absolute (polytropic) calculations.
cₙ; specific heat capacity calculated (and displayed) for the absolute process (only).
Q; quantity of heat transferred during the process.
W; work done during the process, also equal to the mechanical equivalent for the system; e.g. as that generated by a piston.
δS; change in entropy during the process.
δU; change in internal energy during the process.
δH; change in enthalpy during the process.
RAM, SHC
Thermodynamics includes a dropdown list of the 92 natural elements along with their relative atomic masses and their specific heat capacities.
This list is provided for your information and assistance, should you wish to use it.
You simply select an element from the list, and its relative atomic mass (RAM) and specific heat capacity (SHC) will be displayed in the TextBox below as "RAM, SHC".
You may copy & paste the value(s) into the appropriate input values (using 'SHC' as 'cₚ') in your calculation.
Applicability
As stated above, whilst thermodynamics is generally used to describe the transfer of energy in gases, it also applies to solids and liquids, as long as the appropriate - and associated - pressures and volumes are used.
Accuracy
These calculations provide output data (calculation results) as accurate as the data entered.
Notes
- The images provided are for guidance only, they do not imply an exact system nor do they identify the source of losses, which vary considerably, for any system.
Further Reading
You will find further reading on this subject in reference publications(1, 12 & 13)

