Magnetism is described in detail on our dedicated web page for this subject. The practical applications will be described here.

Gravity (potential energy)

Magnetism starts with the magnetic charge, which we today refer to as mass. This non-polar magnetic charge is the source of the potential energy between any two bodies of matter. Gilbert and Newton gave us a solution to this problem well over 300 years ago with their force formula: F = G.m₁.m₂/R², where 'm₁' and 'm₂' are collections of magnetic charges. Newton's solution was in terms of force. Because energy is 'force times distance', potential energy becomes; E = G.m₁.m₂/R.

However, this formula also allows us to calculate the 'gravitational' acceleration exerted on one body by the other; a = G.m/d². For example:
If we enter a mass of 1.9885E+30 kg for 'm₁', and a distance of 1.47095E+11 m for 'd', output 'a₁' will be the gravitational acceleration induced by our sun on the earth at the earth's orbital perigee.
Moreover, if we enter a mass of 5.957863E+24 kg for 'm₂', at the same distance 'd', output 'a₂' will be the gravitational acceleration induced by the earth on our sun, also at the earth's orbital perigee.

This calculation applies to any and all masses, irrespective of their composition and separation (distance). In fact, all the particles in every body of matter radiate potential energy of attraction over a distance of infinity. But the force of attraction will be distributed over the spherical area at the distance between them, i.e.; F = Fₒ / 4πd².
Moreover, the origin of attraction by any collective mass (of atomic particles) is always concentrated at the body's centre of mass. Therefore, 'd' must always be the distance between centres of mass.

Bar-Magnets

A bar magnet is merely a lump of elemental matter capable of attracting a body of ferro-magnetic material. Its magnetism is indirectly due to electrical and magnetic charges.

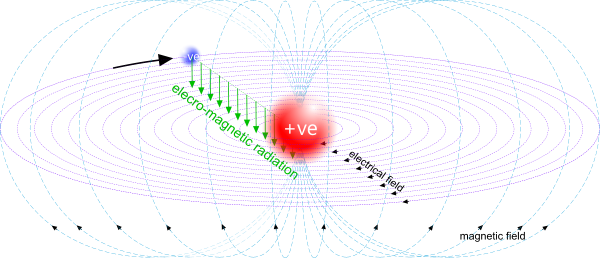
Every atomic particle (in the universe) is either a proton or an electron (see neutron), both of which carry an electro-magnetic charge. If you rotate one electro-magnetic charge about another, you will generate electrical and magnetic fields, and radiate EME. This rotary affiliation is called a proton-electron pair, every atom comprises collections of proton-electron pairs - together with their one or two neutron partners - and nothing else. These electrical and magnetic fields are illustrated in Fig 1. Magnetic fields accrue, increasing their strength if their proton-electron pairs are aligned.

Whilst the electrical fields cannot conglomerate (Fig 1), magnetic fields can. However, in all metallic elements - the natural state of which is random (small crystals) - the magnetic attraction of the collective body is also random, and therefore directionally weak.

Because the strongest fields are generated by an atom's shell-1 (innermost) proton-electron pairs (2-off), alignment of all these (shell-1) proton-electron pairs will cause all their magnetic fields to act together, maximising their field of influence. This is a bar magnet; a body of matter that will influence the behaviour of other magnets and ferro-magnetic matter.

This form of magnetism is polar, but because it is generated by the electrical charge in the element’s atomic particles, it is therefore stronger by the reciprocal of the coupling ratio. However, whilst it is strong, it is unidirectional and has a very limited field of influence.

Some elements exhibit this behaviour naturally, all of which are hcp. But unusually, the shell-1 proton-electron pairs in the bcc element iron can be artificially aligned (semi-)permanently with a lodestone. Very few other elements can be magnetised with a lodestone; e.g. nickel and cobalt, because the ability to do so is entirely dependent upon an element's lattice structure, its RAM and its neutronic ratio; all of which must together permit close to 100% alignment for a magnet to be effective.

Important Note: The result you get here is based upon 100% alignment, which is only possible in a single crystal of pure elemental matter. In fact, this is the reason most elements cannot be magnetised; it is impossible to align a significant percentage of their atoms. But because all natural metals are collections of small crystals, some of which will not align perfectly, you should expect a less-than-perfect strength in most bar magnets; e.g. 60% of the calculated value.

Electro-Magnetic Coils

An electro-magnetic coil is merely a length of wire wound into a coil. Pass a current through it and you will generate a localised field along the wire, wind the coil tightly and you will generate a highly localised field along the coil, turning the coil into an electro-magnetic 'bar-magnet' that will transfer its magnetism to any ferro-magnetic material within its coils. The simplest, and commonest of this type of magnet is the solenoid (Fig 2).

Today we calculate the force induced in an electro-magnetic coil using what CalQlata refers to as calculation 'method-1';
F = μ.(N.I)².A / 2.d²
where 'A' is the cross-sectional area of the coil, 'N' is the number of turns and 'd' is the gap between the end of the plunger and the 'stop'.
In reality, however, 'A' and 'N' play no part in the coil's performance; it is governed by the ratio of wire-length (ℓ) and the gap (d). So it doesn't matter how many turns your coil has so long as the ratio is correct, and when you take electrical resistance into account, the longer the wire and the smaller its diameter, the greater the electrical resistance, and the lower the coil's efficiency.
Moreover, the above formula takes no account of temperature, and as we all know, current only defines electron velocity, it does not tell us how much energy is required to generate it. Voltage, on the other hand, is Joules per second, which is the primary energy generator, and this is dependent upon electrical resistance (I = V/Ω), which is dependent upon temperature. This consideration becomes very important when designing transformers.

Therefore, CalQlata recommends the use of what we call calculation 'method-2', which is based upon Coulomb's and Henry's calculation techniques and includes the effect of temperature. Notwithstanding the above, from a practical standpoint, you should design your coil such that it adequately contains and controls plunger movement (Fig 2).

Magnetism - Technical Help

Units

You must enter your data in metric units; metres, kilograms and Kelvin (and Couloms and seconds), but your output data will also provide conversions to ft and lbf.
note: Amps are Coulombs per second (C/s)

Input Data

The following input data applies to all calculation options:
m₁ = mass-1 [kg]
m₂ = mass-2 [kg]
m = mass [kg]
d = distance between bodies [m]
ℓ = length of wire in coil [m]
A = coil cross-sectional area [m²]
I = applied electrical current [C/s]
Ṯ = temperature of the magnet [K]
Z = atomic number
RAM = relative atomic mass [g/mole]
ε = bar-magnet efficiency

Output Data:

The following output data applies to all calculation options:
F = potential force induced by magnet
PE = potential energy induced by magnet
a = potential acceleration induced by body₁ or body₂ at distance 'd'

Calculation Options

Gravity: Potential force and energy generated by this calculation option are obvious, but it is not quite so obvious for potential acceleration. For example:
enter m₁ = 1.9885E+30 kg & m₂ = 5.957863E+24 kg.
Calculate the gravitational acceleration induced by; our sun on the earth at the earth's orbital perigee, and that induced coincidently by the earth on our sun:
enter; d = 1.47095E+11 m
a₁ = 0.006133233 m/s²
a₂ = 1.8376143E-08 m/s²
respectively.
Calculate the gravitational acceleration at the surface of our sun and the earth:
enter; d = 695710000 m, you will get; a₁ = 274.1755834 m/s²
alter; d = 6367444.5 m, you will get; a₂ = 9.8066314 m/s².
respectively.

Bar Magnets: Whilst temperature is included in this calculation, you should see no change in the force (and energy) in the output data if you alter its value.
This is because magnetism of this type does not vary with temperature. It is included in this calculation option merely to; a) demonstrate this fact, and; b) by way of formula verification.
'd' in this calculation option is between centres of mass.

Electro-Magnetic Coils: The conventional calculation technique we use today (method-1) can only ever be approximate. Not only does it ignore the effect of electrical resistance in the coil, it also ignores the ratio of lengths. For example:
current; I = 1 C/s
wire length; ℓ = 100 m
coil area; A = 0.01 m²
gap (distance); d = 0.01 m
temperature; Ṯ = 300 K
Calculation method-1 (the number of turns (282.1) is calculated):
F₁ = 5 N
Calculation method-2:
F₂ = 8.2025 N
It is up to you which calculation method you prefer.

Applicability

Magnets applies to to any and all bodies of matter, bar-mafgnets and electro-magnetic coils, such as solenoids.

Accuracy

Accuracy depends on the calculation option selected;
'Gravity' is as accurate as the data entered.
'Bar-Magnets' is as accurate as the value entered for efficiency (ε).
'Electro-Magnetic Coils' subscript two (₂) values are more accurate than subscript (₁) values because the latter takes no account of temperature.

Further Reading

You will find further reading on this subject in reference publications^(??)