Mass Density (a working hypothesis)
{Keith Dixon-Roche © 07/07/25}This web page is a moving beast; its content will be updated periodically as a result of future discoveries.
Density is the only feature of elemental matter that we have not yet been able to predict from its elemental properties (States of Matter). We have, however, managed to define its pattern mathematically (Fig 1).
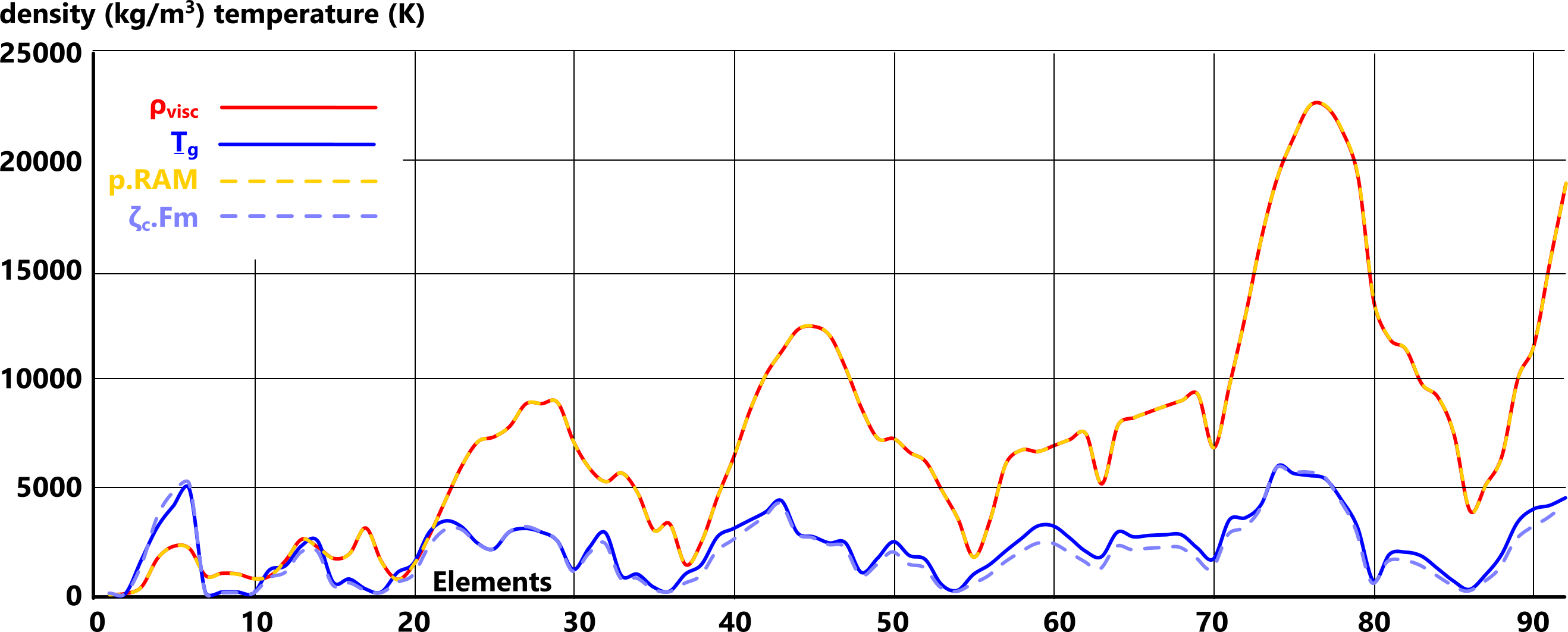
As demonstrated in Fig 1, matter density and gas-transition temperature are related. This is because they are both dependent upon the same inter-atomic forces (Fig 2; Fₑ & Fₘ).
Adjacent atomic elements are attracted to each other by the magnetic field force (Fₘ) generated by their proton-electron pairs.
Adjacent atomic elements are forced apart by the electrical charge force (Fₑ) in their nucleic protons, which varies linearly with temperature.
The neutronic ratio (ψ) of each element determines its nucleic structural (lattice) arrangement, which is replicated in the structural arrangement of elemental atoms in matter, in both gaseous and viscous states.
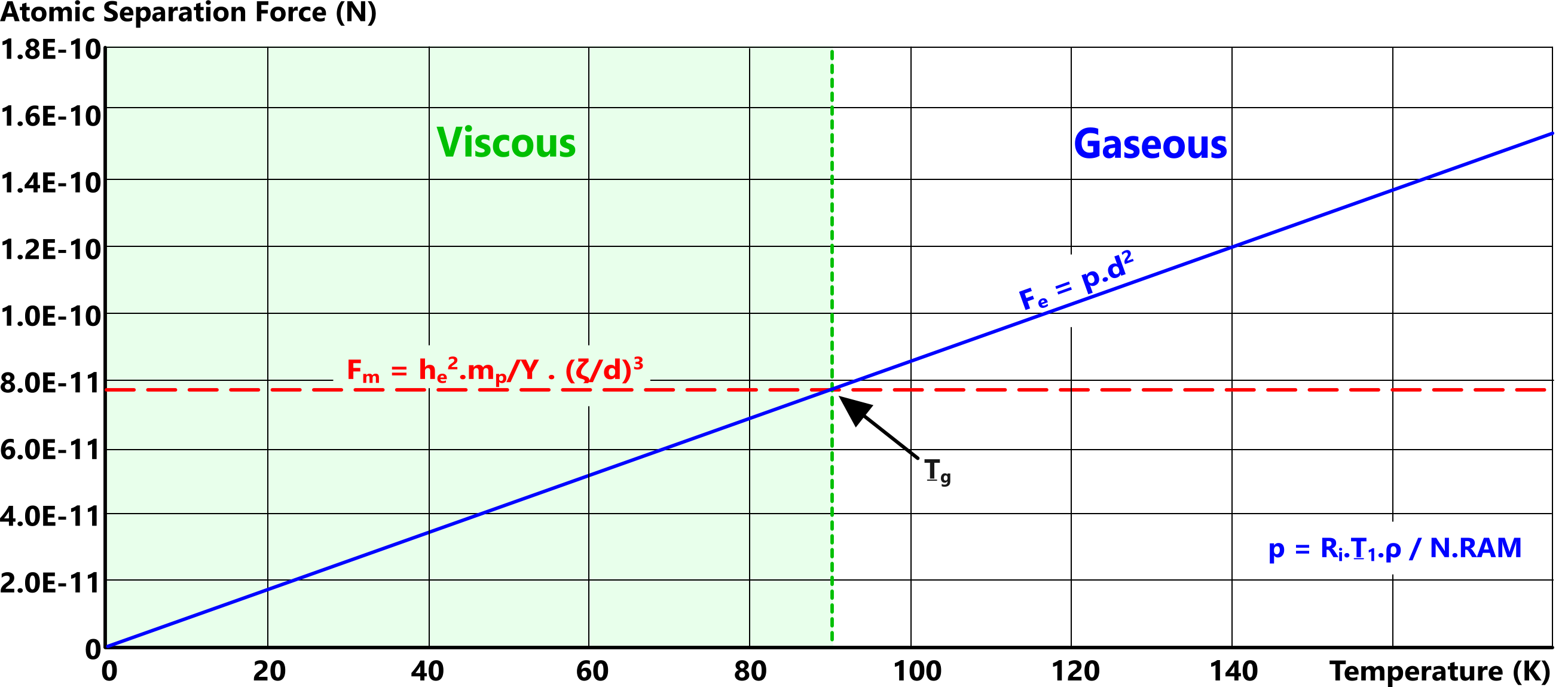
The state of matter is defined thus (Fig 3);
Fₑ < Fₘ: matter will be viscous (liquid or solid),
Fₑ = Fₘ: viscous-gas-transition,
Fₑ > Fₘ: matter will be gaseous.
Whilst the density of viscous matter is [theoretically] constant, raising 'Fₑ' will weaken the strength of attraction between adjacent atoms. This reduction in strength is what causes matter to flow (melt) due to gravity.
Because electron shell radii vary inversely with temperature, if you continue to raise its temperature, eventually the outermost orbital shell radii of elemental atoms will fall below 'd' (viscous atomic spacing), eliminating electron sharing. This is what transforms molecular gas to atomic gas.
Conclusion
This formula demonstrates that inter-atomic forces are defined by a lattice factor:
ζ = ³√[ (d/Rₙ)² . Ṯg/Ṯₙ / ξₘ ]
Whilst 'd' is known, because density is easily established with minimal error;
'ζ' and 'Ṯg' are both dependent variables, so one of these must be defined exactly if we are to solve gas-transition.
Of one thing we can be sure, however, our current understanding of elemental lattice structures is incorrect; 'ζ' differs for every element.
As none of the documented values for 'Ṯg' are likely to be accurate, the answer must lie in Fig 4.
Inter-Atomic Forces
Fig 2 is a plot of the inter-atomic forces - attraction (Fₘ) and repulsion (Fₑ) - of all the natural atomic elements (1 to 92) at three different temperatures; 90.15K, 2329K & 6200K. As we can see, the magnetic force of attraction is [theoretically] constant irrespective of temperature, and the electrical charge force of repulsion varies linearly with temperature. Above 6200K, all elements are gaseous.
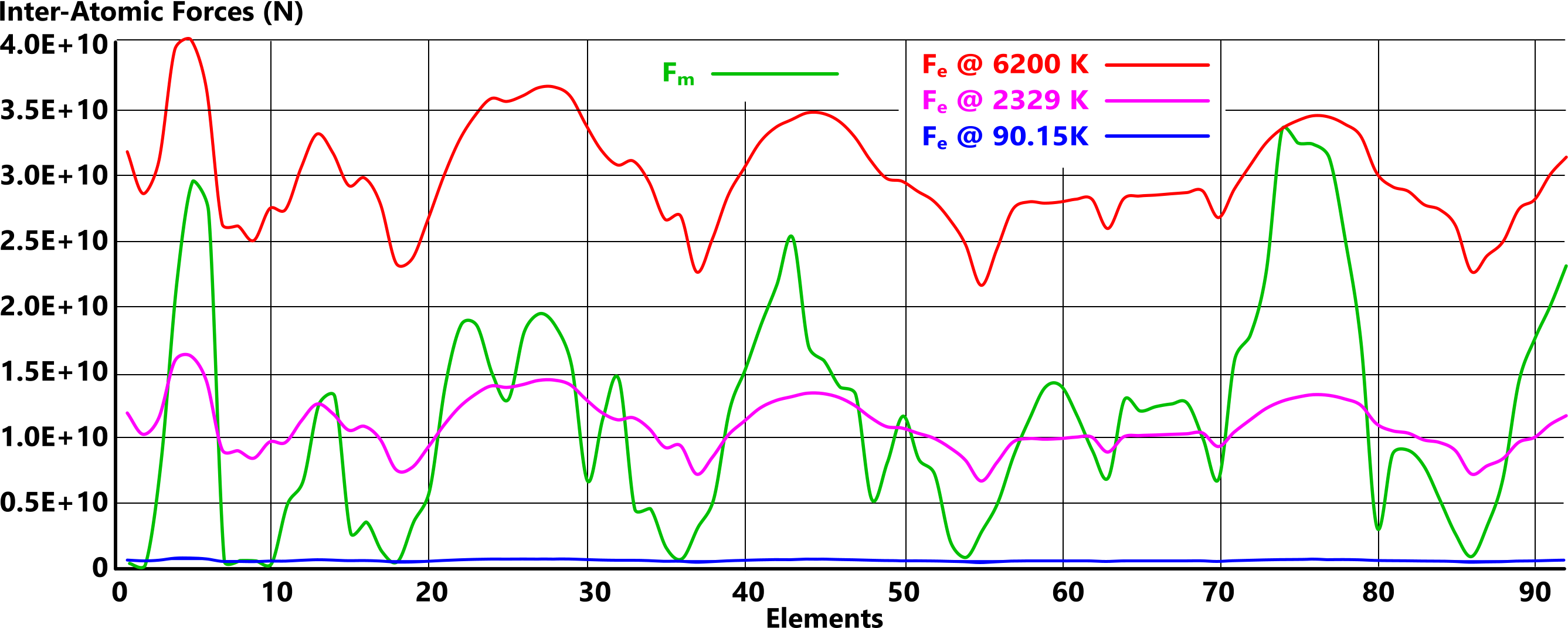
However, we must not forget that there is a subtle difference between a vapour, a molecular gas and an atomic gas;
A vapour is an atmospheric gas that holds globules of molecules or atoms in suspension, so the above temperatures, in many cases, predict vaporisation rather than gas-transition.
When the repulsion electrical [charge] force, exceeds the elemental magnetic [field] force, matter will exist as a molecular gas (e.g. N₂).
When the orbital radius of an elemental atom's outermost proton-electron pair is less than 'd', electron sharing will be lost, and the elemental atoms will exist as an atomic gas (e.g. N).
For example; whilst raising the temperature of nitrogen to 77.3K will cause its transition from viscous to molecular gas (Fₑ>Fₘ), you would need to heat it to more than 4533K to eliminate electron sharing and change it to an atomic gas.
These forces may be predicted mathematically as shown below:
Subscripts:
'ₘ' = magnetic
'ₑ' = electrical or electron
'₁' = innermost shell; shell-1
'ₛ' = outermost shell
The magnetic field force of attraction (Fₘ) between adjacent atoms:
Fₘ = μₒ . Iₛ² . (2π)² . ξₘ/Y . (ζ.Rₛ/d)³ = mₚ/Y . Rₙ⁴/tₙ² . (2π)² . (ζ/d)³ = mₚ/Y . (c.Rₙ)² . (ζ/d)³ = mₚ/Y . hₑ² . (ζ/d)³
As can be seen from the above formula, the variables all cancel out, leaving only constants; hence the constant magnetic force (irrespective of temperature).
Whilst this means that the density of all elements remains constant at any temperature, such a claim is theoretical; it actually falls gradually due to changes in lattice structure, together with weakening attraction as repulsion forces rise with increasing temperature.
The electrical force of repulsion (Fₑ) between adjacent atoms:
Fₑ = p.d²
Fₑ = PE₁ / Y.d
Fₑ = μ₁.I₁².(2π)² / (d.Y/R₁)
Fₑ = k.e'₁² / (d.Rₙ.FT)
All of which give exactly the same value for any element at any temperature.
Where:
Iₛ = electrical current in the proton-electron pair
Rₛ = electron orbital radius
d is the average inter-atomic spacing (³√[mₐ/ρ])
ζ = lattice factor
p = internal pressure (PVRT)
μₛ = mₑ.Rₛ/e²
R₁ = electron orbital radius
I₁ = electrical current
e'₁ = proton electrical charge
Ṯ₁ = proton-electrical pair temperature
Ṯₖ = temperature constant (Ṯₙ / Y.ξₘ = 19.4336001664707 K)
FT = Ṯ₁/Ṯₖ
Both density and gas-transition temperature may be found from the magnetic field attraction force between adjacent atoms (Fₘ) thus:
Ṯg = Fₘ.d . ξₘ.X.Y / mₚ
ρ = Fₘ . Y/hₑ² . RAM/ζ³ . mₙ/mₚ
Lattice Structure
The lattice structure of elemental matter defines its density and its gas transition temperature. It is specified for each element by name, which represents a 3-D arrangement of its atoms. However, this same arrangement originates in an element's nucleus, and is replicated in elemental matter in both viscous and gaseous states.
Lattice factor 'ζ' applies @ Ṯg when Fₘ = Fₑ:
1 = Fₑ/Fₘ = (k.e'₁² / (d.Rₙ.FT)) / (hₑ².mₚ / Y.d³) / ζ³
ζ = ³√[ (k.e'₁² / (d.Rₙ.FT)) / (hₑ².mₚ / Y.d³) ]
ζ = ³√[ (Y.k.Ṯₖ) / (Rₙ.hₑ².mₚ) . (mₚ.RC.Ṯg/Ṯₙ)² . d²/Ṯg ]
ζ = ³√[ (d/Rₙ)² . Ṯg/Ṯₙ / ξₘ ]
ζ³ = (d/Rₙ)² . Ṯg/Ṯₙ / ξₘ
d² = ζ³.Rₙ².Ṯₙ.ξₘ / Ṯg
d = Rₙ. √[ Ṯₙ.ξₘ . ζ³/Ṯg ]
ρ = mₐ / [ (ζ³ . hₑ².mₚ.Ṯg.Rₙ) / (Y.k.e'₁².Ṯₖ) ]¹˙⁵
ρ = mₐ / [ (ζ³ . hₑ².mₚ.Ṯg.Rₙ) / (Y.k.(Ṯ₁ . ξₘ.e/Ṯₙ)².Ṯₖ) ]¹˙⁵
ρ = mₐ / [ (ζ³.Ṯg . hₑ².mₚ.Rₙ.Ṯₙ²) / (Ṯg² . Y.k.ξₘ².e².Ṯₖ) ]¹˙⁵
Optimise the constants in the above formula
Constant Λ = (hₑ².mₚ.Rₙ.Ṯₙ²) / (Y.k.ξₘ².e².Ṯₖ) = ξₘ.Rₙ².Ṯₙ = 9.0882370009374E-18 {m².K}
The relationship between matter density and gas transition temperature is therefore:
ρ = mₐ / [ Λ . ζ³/Ṯg ]¹˙⁵
Ṯg = (ρ/mₐ)⅔ . Λ.ζ³
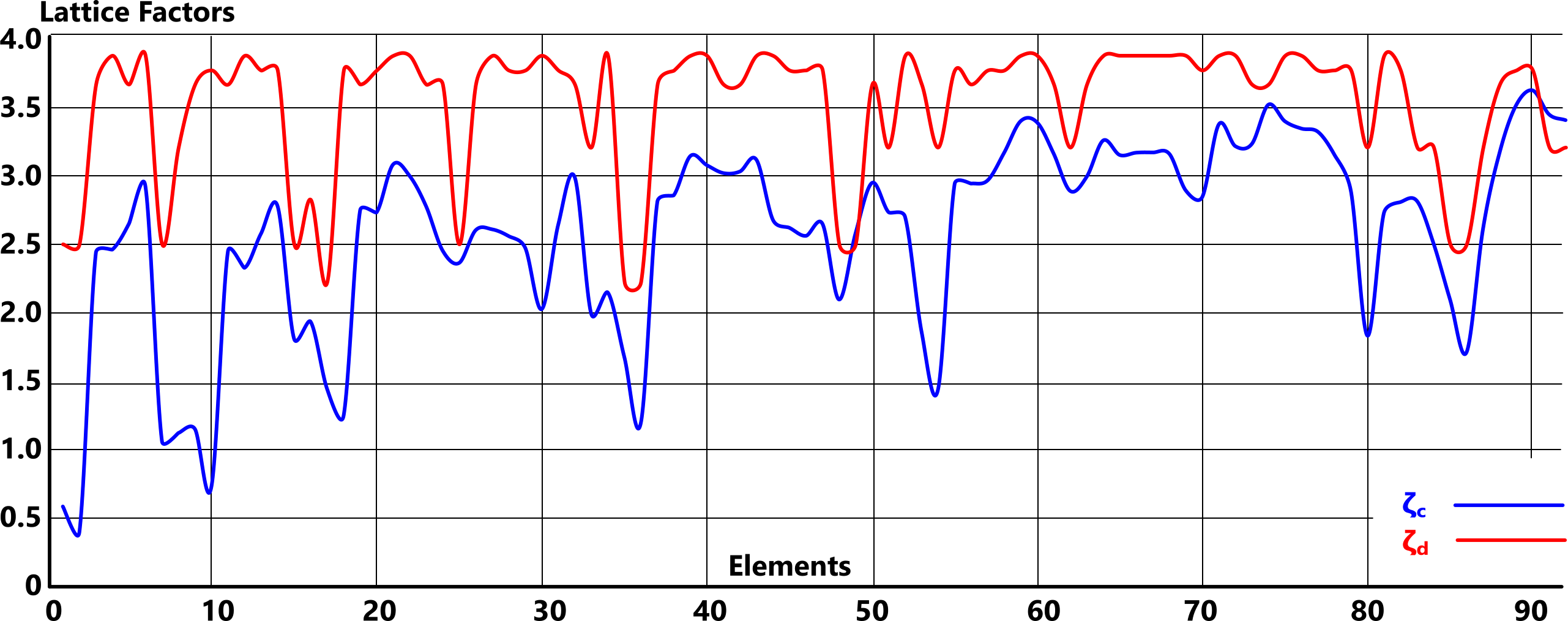
Whilst there is an unmistakeable relationship between the documented lattice structures (some of which vary with source) as is evidenced in Fig 4, the actual (calculated) values reveal that they are simplistic; every lattice structure (ζ) is different.
The numerical values for each documented lattice structure, which define the elemental atoms are listed below:
bcc; 2.5
cubic; 3.25
cubic+2; 3.5
fcc; 2.45
hcp; 2.4
hcp+3; 2.5
monoclinic; 2.75
orthogonal; 2.5
rhombic; 2.75
rhombic+2; 3
tetra; 2.75
Discussion
Fig 1 shows us that the density and gas-transition temperature of elemental matter are related.
Figs 2 & 3 show us that the inter-atomic forces between adjacent elemental atoms reveal their gas transition temperature.
The mean separation distance (d) between adjacent elemental atoms defines their density as viscous matter; mₐ/d³, and their magnetic force of attraction (Fₘ) between adjacent atoms. Fₘ does not vary with temperature.
The positive electrical charge held by all nucleic protons (e') generates a repulsion force (Fₑ) between adjacent atoms, that varies linearly with temperature.
It is the difference between these forces (F = Fₑ - Fₘ) that determines whether elemental matter exists in a gaseous or viscous state.
The melting point of any elemental matter simply tells us above which temperature it can no longer hold its shape under the influence of the gravitational forces to which it is exposed; i.e. when it will begin to flow.
The idea that a block of cold iron is viscous may seem odd to us, but it is perfectly valid; for example it would flow as a liquid at the surface of a galactic force-centre.
In other words; the melting point of any matter you find in any reference document only applies at sea-level on the surface of the earth. It will be different everywhere else in the universe.
However, the lattice structure of an elemental atom is fixed; it is defined by the arrangement of its deuterium and tritium nucleic protons. Therefore, the viscous density and gas-transition temperature of matter are theoretically constant anywhere throughout the universe, apart from the influence of atmospheric pressure.
But its melting point will vary.
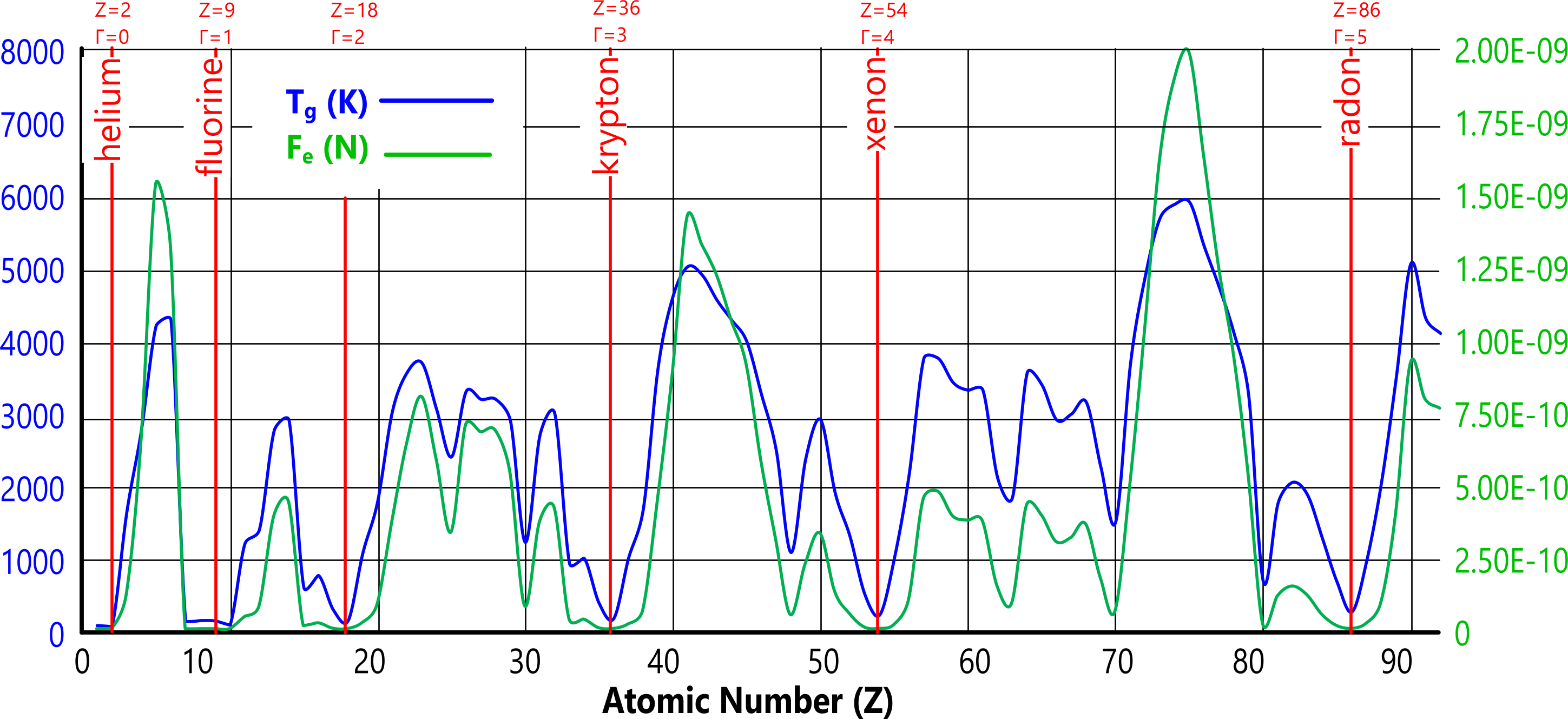
Fig 5 demonstrates that an unmistakable relationship exists between an element's neutronic ratio (ψ) and its density and gas-transition temperature. As we can see; the gamma function; Γ = 9.(ψ-1), which reveals the noble gases (albeit fluorine instead of neon), is dependent upon 'ψ' and the factor 9. It would appear therefore, that 9 constitutes a limiting nucleic group for an element's deuterium and tritium atoms.
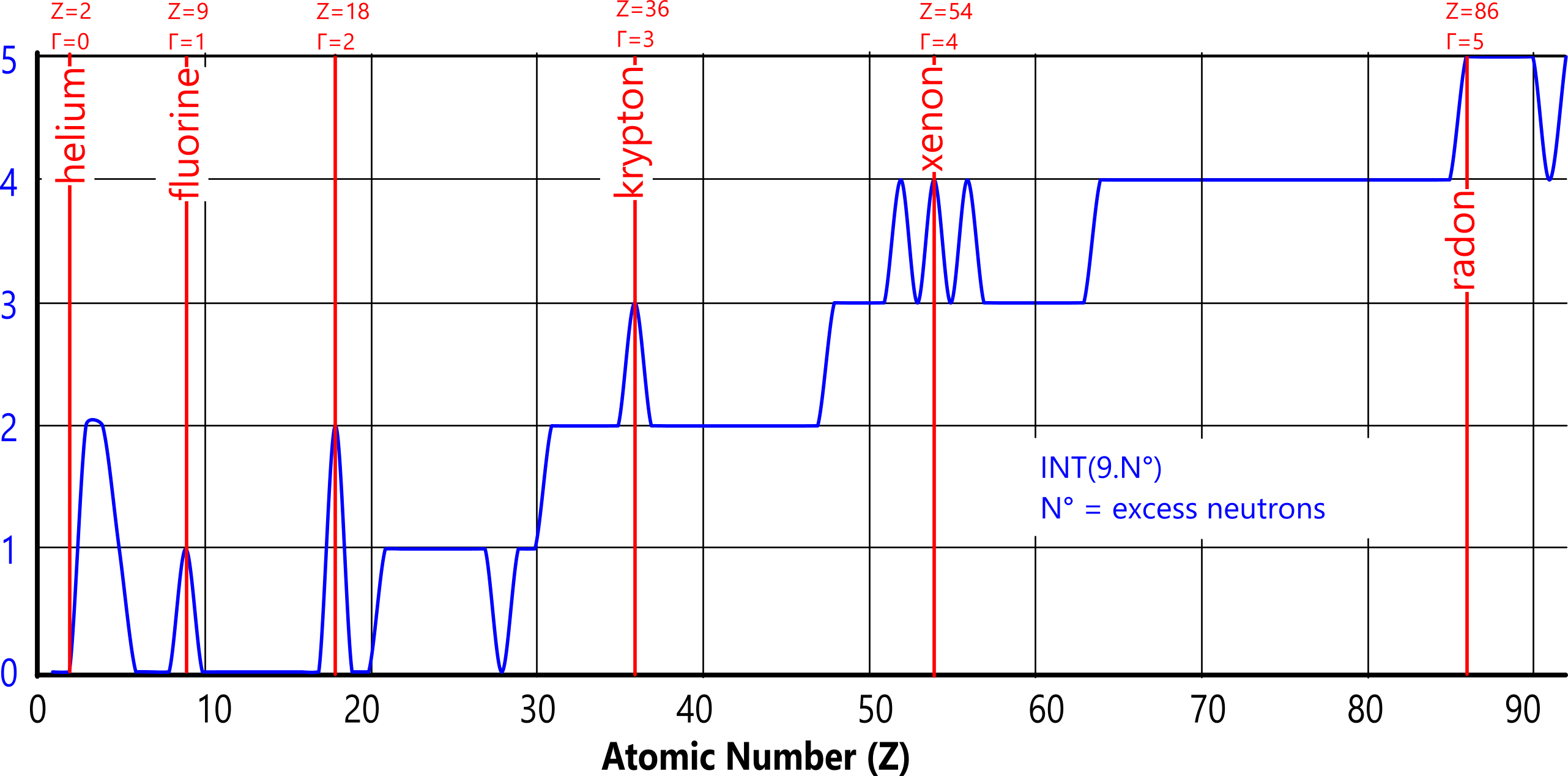
This prominence appears again if we plot (Fig 6) the integer values for the number of excess neutrons (tritium atoms), in which the same elements are the first to jump to the next integer, except for tellurium and barium which uniquely possess an even higher percentage of neutrons (RAM/Z-2) than xenon.
Further Reading
You will find further reading on this subject in reference publications(69, 70, 71 & 73)