Core Pressure Calculator
This web page and the maths associated with this calculator are copyright protected by
Keith Dixon-Roche {© 08/11/17}
Core pressure is the pressure inside an astronomical body (Fig 1: the earth).
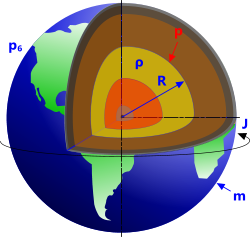
Fig 1. Structure of a planetary body
The core pressure of any planetary body can be estimated from its polar motion of inertia, which can be established from Isaac Newton's laws of motion and Spin Theory. Once known, the density of its various layers (inner-core, outer-core, mantle, crust) can be generated to reproduce the calculated polar moment of inertia.
Newton's famous formula (F = G.m₁.m₂/R²) for gravitational attraction may be applied to any internal radius to establish the force imposed by the mass of material outside the radius (R); m₁ being the mass of material inside 'R' and m₂ being mass outside it.
Newton's formula only allows us to calculate internal pressure due to gravity, it is necessary to apply thermodynamics to determine the additional internal pressure from heat.
From the various layer-densities it is also possible to estimate the elements it comprises.
Core Pressure Calculator – Technical Help
Cores provides for up to 6 internal layers, the interface radii and densities of each must be iterated until the two factors (Fm & FJ) equal 1.0, after which the mass and polar moment of inertia will be representative of the astronomical body being investigated.
Units
You may use any units you like, but you must be consistent.
Input Data
R₀ to R₆ are the interface radii. R₀ is the inner-most radius such as that of a proton. The pressure here is pretty meaningless but setting R₀ to 0 will generate a zero pressure due to m₁ also being zero. It is also recommended that R₁ should be about 1m as the inner-most practical radius. R₆ must the outside radius of the planet.
ρ₀ to ρ₆ are the interface densities. ρ₀ is the inner-most density. The density of each layer will be assumed to vary linearly between each interface. If the innermost density is that of a proton, it should be set to that of proton (i.e. 7.12661E+16 kg/m³). ρ₆ must the average density of the planet's surface material.
m is the known mass of the astronomical body
J is the known polar moment of inertia of the astronomical body (e.g. kg.m² or lb.in²)
p₆ is the atmospheric pressure at the surface of the astronomical body
G is Isaac Newton's gravitational constant
Output Data
Fm is the mass factor that must equal 1.0 for the calculation to be correct
FJ is the polar moment inertia factor that must equal 1.0 for the calculation to be correct
p₀ to p₅ are the pressures at each internal interface (gravitational only)
Applicability
The Cores calculator is applicable for any astronomical body
Accuracy
The accuracy of Core's output is commensurate with the data entered. The closer Fm and FJ are to 1.0 the more representative the calculation result.
Further Reading
You will find further reading on this subject in reference publications(55, 61, 62 & 64)

