Lift Rigging Calculator (2, 3 & 4 Legs)
When using a lifting system to lift and move a body (mass) from one place to another, it is essential that you know the exact dynamic loading conditions to which it will be exposed or that you apply suitable safety factors to accommodate your unknowns. It is also important to remember that all lifts are dynamic, no matter how slow the speed of movement.
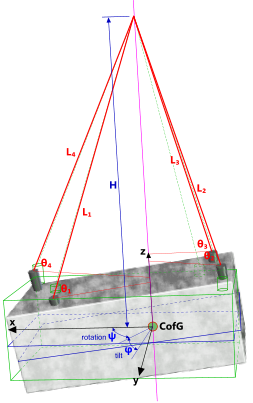
Fig 1. Typical Lift Rigging
In a configuration where all legs are of exactly the same length and connected to the mass equidistant from the centre of lift and from each other and connected to the lift wire at the same point, the load in each leg will be the same and the body should lift 'flat and even' off a stationary terrain. Otherwise the load in each leg will vary.
If the legs are not of correct length according to the lift point positioning, the body will suffer from uncontrolled tilt, which is never acceptable (see Safety Factors; Quality below). Where a tilted lift is desirable, i.e. the body is to be placed on a tilted surface, the unevenness of the leg lengths should be determined by calculation and the system (leg lengths) should be manufactured accurately.
It is usual to install a mechanical turnbuckle in at least one of the legs in a four-leg system in order to ensure equally distributed loads or to lift your mass using a three-leg system, which always distributes loads evenly between each leg according to its horizontal distance from the CofG.
A dynamic amplification factor must always be applied to your static weight, and a safety factor must always be applied to the strength capacity of your lifting system (see Dynamic Amplification Factor and Safety Factor below).
Dynamic Amplification Factor (DAF)
A dynamic amplification factor is a value (greater than 1.0) by which you multiply your static weight in order to determine the total dynamic load you should expect in your lifting system.
A DAF must always be applied to this weight in order to account for even the minimal dynamic amplification induced by the speed of the winch. At worst, the accelerations and winch-wire velocities of a crane and or mass such as located on a moving base (e.g. a ship at sea) must be included in your calculations.
Typical DAF Calculations
Three example calculations for DAF are provided below ('g' is gravitational acceleration ≈9.8066m/s²):
1) A static crane lifts a mass from solid ground using a 4-leg lifting system with the load equally distributed between each leg:
Winch operating speed (v) is 0.3m/s (≈17 seconds to raise a load 5m)
Young's modulus (E) for the wire rope (see CalQlata's Wire Rope calculator) used for your lifting legs is 2.7E+10N/m²
The length (L) of the leg under consideration is 2.7m
The cross sectional area (A) of the lift wire (including gaps) = 0.00018m²
The maximum static tension (T) in the lift leg under consideration is 2,750N
The extension (d) in the lift leg at the applied load is calculated thus:
d = T.L ÷ A.E (from; E = σ/e) = 2750 x 2.7 / 0.00018 / 2.7E+10 = 0.00156m
Acceleration (a) of the applied load (at pick-up) is calculated thus:
a = (v² - u²) ÷ 2.d = (0.3² - 0²) / 2 / 0.00156 = 28.92m/s²
The resultant dynamic amplification factor for initial pick-up is therefore:
DAF = 1 + a/g = 1 + 28.9/g = 3.95
After pickup, the DAF drops to:
U = ½.m.v² = 0.5 x 2750/g x 0.3² = 12.62N.m
Thus assuming maximum velocity (0.3m/s) is applied to the winch prior to, during and after pick-up, the initial DAF of 3.95 will drop to 1.0046 thereafter. This is recognised as a 'snatch load' and means you need to ensure that; either your lifting system is capable of handling the snatch DAF or that your crane operator is careful to apply a lower winch speed at initial pick-up.
2) A ship's crane lifts a mass off the deck of another ship sitting alongside whilst at sea:
Assume the same crane and lifting system as that in example calculation 1) above.
The total vertical movement⁽¹⁾ (d) of the crane is 4m over a period (t) of 8 seconds for each ship (see CalQlata's Velocity & Acceleration & Vessel Motions calculators), for reasons of conservativeness (worst-case-scenario) it is necessary to assume that both vessels will move simultaneously in equal and opposite directions at the time of lift:
The winch speed must be such that the load can be raised a height of 8m (2.d) in at least 8 seconds i.e. v = d/t > 8/8 > 1m/s
In this case the above DAF value for post pick-up conditions is modified thus:
a = (v² - u²) ÷ 2.d = (1² - 0²) / 2 / 8 = 0.0625m/s²
DAF for the winch is therefore; DAF = 1 + a/g = 1 + 0.0625 / g = 1.00637
The same snatch load considerations apply to this scenario.
If the maximum expected vertical accelerations (av) for both ships at the moment of pick-up are an equal and opposite 2.3m/s², the DAF due to opposing vessel accelerations will be DAF = 1 + 2.av / g = 1 + 2 x 2.3 / g = 1.469
Of the three potential DAF values in an operation such as this; 3.95, 1.00637 & 1.469 the snatch load DAF (3.95) is still the worst-case scenario and this margin provides sufficient allowance to compensate for the unknown factors (due to weather and relative vessel movements) in the other two operations.
3) Assume the same lifting vessel as that described in example 2) above is lowering the body into the sea in the same conditions and no constant tension or heave compensation system is fitted to the crane winch:
The winch speed is usually ignored in such calculations as; a) the associated DAF is negligible compared to the added mass and drag (see CalQlata's Added Mass & Drag calculator) applied to the load and the winch is paying out so the loads will be reduced. On the other hand, if the load is being raised through the water column, winch speed should not be ignored.
The vertical acceleration applied to the load (and hence the lifting legs) is the sum of the coincident accelerations of; gravity, wave water (see CalQlata's Ocean Waves calculator) and vessel (a = g+av).
In addition to the above, the effect of displacing water around the immersed body must be considered. For the purposes of this calculation example, we shall assume the total vertical acceleration in the vessel (a) is 14.4m/s:
F = m x a + FC
where FC is the force due to drag and added mass (see CalQlata's Fluid Forces calculator)
If we apply values of 280N and 260N for the drag force and added mass respectively to the 1000kg mass in example 1) above we get a total Force; F = 1000 x 14.4 + 280 + 260 = 14,940N (÷ 4 for each leg)
The resultant dynamic amplification factor is: DAF = F / W = 3,735 / 2,750 = 1.358
As with calculation example 2) above, it is advisable to increase the above DAF (1.358) by a suitable factor to account for unknown weather conditions. However, also as with calculation example 2) above the DAF for the snatch-load provides sufficient allowance to compensate for the unknown factors in this operation.
Note: When raising the mass up out of the water, the winch speed should be such that the lifted mass is raised fast enough to avoid being hit below by a rising wave as it passes through the splash zone because it will drop again as the wave passes increasing the above DAF.
Sheave Blocks
When using a sheave block in the lift system, remember to reduce the lift speed according to the number of pulleys it contains and the associated DAF accordingly. For example; a 6-Pulley sheave block will reduce the lift speed by a factor of 12.
Safety Factor (SF)
Safety factors must be applied to the strength rating of your lifting legs, and the value of your safety factor should depend on a number of considerations (see Typical SF Calculation below):
The number of lifts the system will be expected to make during its design life
The accuracy with which you know the loading conditions for all lifts; incl. the DAF
The storage and maintenance conditions that shall be used
The consequences of a lift failure
The number of legs in the lift system
The quality of your components (legs, sheave blocks, wire ropes, hooks, shackles, padeyes, etc.)
Relevant design code or operating guidelines
Number of Lifts: The greater the number of lifts the system is expected to make the more unlikely you will be able to maintain total control over the operating load for each and every operation
Load Accuracy: If your lifting condition is known exactly you need not increase the safety above the minimum required for 'Quality'. Calculated weights that involve unknown factors such as; weather and/or a moving crane and/or load at the time of the lift will require an SF greater than 1.0
Storage and Maintenance: No consideration need be made if these conditions are totally controlled such that negligible deterioration can be assured during the design life of the system. However, you must assess the probable type and level of deterioration for systems stored in-the-field and apply a suitable safety factor to account for it.
Consequences: If the consequences of a component failure are unacceptable, then the SF should be high. If there are minimal consequences then the SF can remain low
Number of Legs: The higher the number of legs in the lift system the smaller the required SF
Quality: The components comprising your lifting system will define the lowest SF you should apply. I.e. the calculated SF required for your system must be lower than the smallest safety factor of any constituent part. It is also important that the leg lengths are manufactured accurately, otherwise at least one of them will be redundant and all the lift-load will be shared between fewer legs than for which the system has been designed; turnbuckles are normally installed in at least one leg to allow for leg-length adjustment.
Codes and Regulations: The safety factor of your system should be no less than that required by the authority's regulating the operation
Typical SF Calculation
CalQlata suggests the following approach for determining your design SF:
One lift; SF=1, unknown number of lifts; SF = 1.5#
Absolute accuracy; SF = 1, unknown lift conditions; SF = 2#
Clean, dry, oiled, protected conditions; SF = 1, left in weather and unprotected; SF = 5#
Failure consequences unimportant; SF = 1, serious; SF = 1.5#
1-leg; SF = 2, 4-legs; SF = 1⁽²⁾#
design SF ≤ minimum component SF
design SF & component SF ≥ minimum relevant design code or operating guidelines
Note: # values may be interpolated for intermediate conditions
The following shall be assumed for these example calculations:
minimum required SF according to the relevant design code or operating guidelines = 4
component parts for lifting equipment are normally designed with a safety factor of 5:1
1) A 3-leg lifting system in 'as-new' condition is to be used for a single lift in well-known conditions with serious consequences of failure: 1 x 1 x 1 x 1.5 x 1.33 = 2
Action: No action needs to be taken as the system complies with all necessary requirements ##
2) A 4-leg lifting system that has been left outside under a tarpaulin in a cold wet environment for 12 months with no attention is to be used for 10 lifts in fairly well known operational conditions and failure consequences are not serious⁽³⁾: 1.1 x 1.2 x 4 x 1 x 1 = 5.28
Action: Assume in this case that you have no way of testing the lift rigging before use. By improving your knowledge of the lift conditions, you can reduce the associated factor from 1.2 to 1.1 bringing the design SF down to 4.8, which would appear to be the simplest corrective action. The system now complies with all necessary requirements ##.
3) A 12 months old 2-leg lifting system that has been stored in dry conditions but unattended is required to carry out 50 lifts in unpredictable conditions with serious consequences of failure: 1.3 x 2 x 2 x 1.5 x 1.66 = 12.95
Action: A number of things can be done to reduce the design SF: a) Improve your knowledge of the lift conditions by reducing your weather window; b) increase the number of legs in the lifting system, c) reduce the seriousness of the consequences of failure⁽⁴⁾ and d) test (certify) the lifting equipment before use; e.g. 1.3 x 1.5 x 1.1 x 1.2 x 1.33 = 3.42. The system now complies with all necessary requirements ##
Note: ## Compliance is demonstrated as the component SF for the manufactured lifting system is greater than those required for operation and the regulatory authority
Typical design codes such as those referenced at the foot of this page provide formulas calculating their minimum requirements. However you establish your safety factors they must fall within the design code requirements that are imposed by the regulatory authorities. The above procedure has been formulated to enable you to make the necessary adjustments to do this.
Lift Rigging Calculator – Technical Help
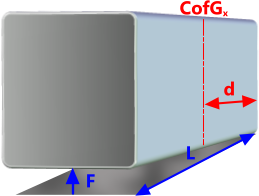
Fig 2. Measure/Calculate CofG
Units
You may use any units you like, but you must be consistent.
The Theory
The position of the CofG within a body must be known, or estimated as accurately as possible, in order to use the rigging calculator. Fig 2 shows a method you can use to determine the CofG in the x,y plane relatively easily.
Lift one end (x-axis) of the mass (of length; L) off the ground and record the force (F) required for the lift . The distance to the centre of gravity is calculated thus; d = F x L ÷ WRepeat this exercise at one side of the mass (y-axis)
You will have to estimate the CofG in the vertical direction (z) by looking at the components immediately above the x=0,y=0 position established above and estimate the height of the centre of mass of the heaviest component(s).
Weight: The weight of the body must include any expected DAF (see Dynamic Amplification Factor above).
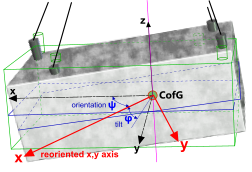
Fig 3. Reoriented (ψ) x,y axis
Dimensions: The x,y dimensions to each lift point and the height (H) to the common connection point on the lift wire (Fig 1) must be entered from the CofG of the body to be lifted along the pre-oriented x,y axes (ψ=0).
Dimension z is always in the same vertical direction, both before and after tilt-orientation and also passes through the CofG of the lifted body (Fig 3).
Tilt: The vertical tilt-plane always passes through the x-axis at y=0. If the orientation of the tilt plane (ψ) is not zero the tilt plane will pass through the reoriented x-axis (Fig 3). The angle of tilt (φ) is negative as shown in Fig 3 (pointing downwards).
As the overall dimensions of the lifted mass are unimportant in Rigging calculations (i.e. you only need the co-ordinates of the lift-points), you may set the direction of the x axis wherever you like relative to the lift-points, in which case you can set the x-axis in the direction of the tilt plane and leave ψ set to zero. For a regular shape, however, such as a container, you will probably find it simpler to enter the x,y co-ordinates in-line with the body and enter an orientation angle for your required tilt.
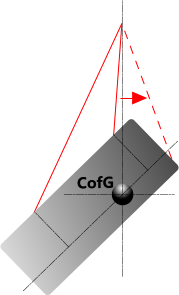
Fig 4. Unreal Lift
The x,y,z co-ordinates listed at the bottom of the Data Listing window, below the output data, relate to the reoriented (ψ) x,y axes, which remain in the horizontal plane and with the same origins (x=0,y=0) as the original axes (Fig 3).
If all these co-ordinates in any direction (x or y) are positive or all are negative, this means that the tilt angle is too great and the CofG has fallen outside the foot-print of the lift points (Fig 4). In which case, the results are unreal and the rigging calculator will provide a warning to this effect.
You must ensure that the tilt you apply is such that the CofG does not fall outside the foot-print of the lift points in both the x and y directions as this will result in an unreal lifting condition.
If you need to lift at this angle, you should reposition your lift point(s) as shown in Fig 4.
An unreal lift condition will also apply if any of the resultant forces (F) are negative. In this case, the load is not distributed to all the legs. You can correct this problem by repositioning the x,y,z co-ordinates of one or more of your lift points.
Accuracy
The results from this calculator are totally accurate according to the dimensions you enter. You must ensure, however, that any tilt you apply is practical, otherwise whilst the results will be correct, they will be unrealistic or unreliable (see Fig 4). Rigging will inform you if the conditions applied result in a lift such that shown in Fig 4
Applicability
The rigging calculator applies to 2-leg, 3-leg and 4-leg lifting systems only. The legs can be manufactured from wire, natural or synthetic rope, chain or manufactured from rigid material. These results also apply only to legs manufactured to correct lengths. Misalignment or incorrect lengths will result in increased loading conditions in the other legs. It is recommended that suitable turnbuckle(s) be installed in at least one leg in order to correct inaccuracies.
Notes
- Twice the RAO of a vessel
- A safety factor of less than 2.0 only applies to legs of accurate manufactured length and/or with turnbuckles that have been adjusted to create accurate leg-lengths
- If lifting equipment has been left unattended for a considerable time in conditions that will deteriorate its materials it is always better to test the system in controlled conditions before use
- Many things can be done to reduce the consequences of an accident; e.g. protect vulnerable equipment; ensure replacement parts and equipment are readily available in the case of an accident; if possible, perform most of the lift away from vulnerable area(s), etc.
Further Reading
You will find further reading on this subject in reference publications(36 & 37)

