Stress
Stress and pressure have the same units for a very good reason; they are the same thing: 'force over area'.
σ = p = F/A
Pressure
The conventional perception of pressure is the application of a [normal] force over a given area of matter (viscous or gaseous).
Internally, the atoms within matter are;
a) held together by their constant attractive magnetic [field] force (Fₘ), and;
b) pushed apart by their repulsive electrical [charge] force (Fₑ), which varies proportionally with temperature.
Therefore, the force (F = Fₘ-Fₑ) holding matter atoms together (viscosity) decreases with increasing temperature.
When Fₑ is less than Fₘ matter will exist in its viscous form (solid and/or liquid), otherwise, it will exist as a gas, but external pressure may be equally applied to it in either condition.
In the case of a 'solid' body, it is assumed that this pressure is applied uniformly throughout all of its atoms. Such uniformity is of course, impossible in the real world. Therefore, the theoretical strength (YS & UTS) of a [solid] body must be significantly higher than its actual strength.
Lattice Structure
It is a fundamental law of nature that all bodies settle at their lowest energy condition. In atoms, this energy refers to the potential energy between neighbours, which is defined by their inter-atomic forces (F = Fₘ-Fₑ) and their separation distances (R):
E = F.R
The atomic structure of elemental matter - how the atoms naturally arrange themselves - is defined by the atom's nucleic arrangement. This is why atoms with similar (but not the same) proton-neutron populations may have very different properties. Their respective inter-atomic forces and radial separations may vary much more than their atomic numbers would suggest.
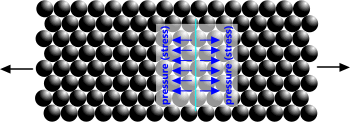
Fig 1. Atoms Under Tension
An atom's nucleic protons and neutrons will organise themselves in such a manner that they exist at their lowest energy level, and also the reason why lattice structures may change with varying temperature affected forces (Fₑ).
The lattice structure of matter represents an atomic arrangement at its lowest energy level; each of which is unique for each element.
Stress
Tension: pulls adjacent atoms apart (Fig 1).
Compression: pushes adjacent atoms together.
Shear: sliding one atomic plane over its neighbouring plane (Fig 2).

Fig 2. Atoms Under Shear
Shear represents the least resistance to relative movement between adjacent atoms because it relies on sliding atomic planes over each other; imagine sliding a load up-hill (shear) as opposed to lifting it vertically through the same height (tension).
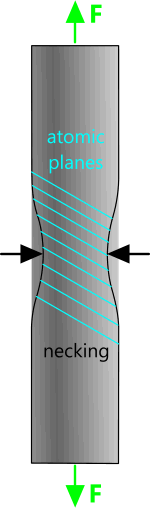
Fig 3. Tensile Necking
The 'elastic range' of matter represents a range of stresses that can be released such that the atoms return [exactly - theoretically] to their relative pre-stressed position; i.e. the matter remains unchanged.
As a body is stretched (or compressed) beyond its elastic limit, the atomic planes rotate as the atoms settle at a new lowest energy condition and slip occurs between adjacent planes due to shear, thereby reducing the material's ability to resist displacement for a given applied stress; this is referred to as plastic deformation. Excessive slippage is responsible for necking of the body under tensile load (Fig 3).
As soon as a crystal of viscous matter is annealed, tempered or work hardened, its structure is modified, altering its resistance to pressure (tensile and compressive). The reason drawing matter through a die increases its UTS, is because this process lines up the atomic planes, reducing average atomic spacing (R).
The generic stress-strain curve (Fig 4) shows two regions of resistance; elastic and plastic.
The elastic region occurs whilst the separation distance (R) is sufficiently small to prevent plane slippage. After 'R' has achieved sufficient separation, the atoms may slip from their original position, causing plastic deformation of the matter.
When a body is stretched (or compressed), no matter by how much, its cross-sectional area must reduce (or increase) accordingly. During elastic deformation this reduction [theoretically] occurs evenly throughout its length. During plastic deformation, cross-sectional reduction occurs unevenly in the body's weaker areas, ultimate failure occurring at its weakest. This is what occurs during necking (or permanent deformation).
Failure invariably occurs at a neck because the tensile stress increases significantly faster as the cross-sectional area of the body reduces.
It is impossible to carefully pull the atoms in a body beyond their elastic limit and carefully release them exactly to their pre-stressed positions because, at their elastic limit, lowest inter-atomic energy configuration changes and plane rotation begins to occur.
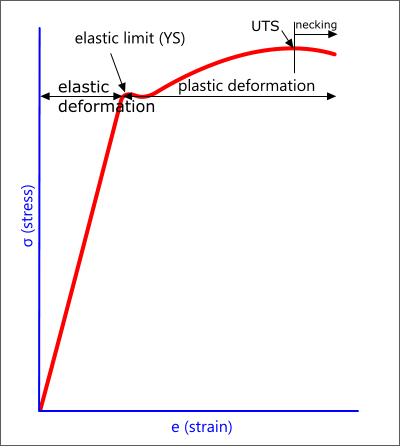
Fig 4. Stress-Strain Curve
Tensile Modulus
The tensile modulus of a substance is dependent only upon the magnetic [field] force (Fₘ), and is therefore constant, irrespective of temperature.
Poisson's Ratio
Poisson's ratio is perceived as the ratio of lateral and longitudinal displacement during elastic deformation. This must mean that the densities of dissimilar metals must vary differently under the same load. But why?
Poisson's ratio of manganese is claimed to be 0.24 and that for copper is 0.34, meaning that manganese must be more brittle than copper because under the same load it will displace laterally less.
In other words; for the same induced stress (σ), the forces (Fₘ & Fₑ) and separation distances (R) must vary considerably more than their relative atomic masses would suggest:
ν; 1.43
Z; 1.16
This discrepancy may be explained by their structural variations.
Different atomic structures will result in different inter-atomic energies and different lowest-energy planes.
For example:
manganese; BCC
copper; FCC
Because the structures are different, the average radial separation between adjacent atoms will also differ, resulting in different resisting energies. This is the reason their UTS values differ more than their atomic numbers would suggest:
Manganese: 650 MPa
Copper: 514 MPa
The ratio of which is 1.26; a compromise!
Poisson's ratio (ν) is therefore dependent upon the body's atomic - or lattice – structure (Fig 5).
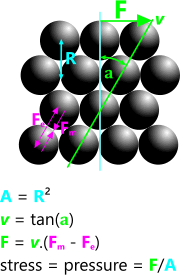
Fig 5. Poisson's Ratio
Calculations
The magnetic force, which is constant, may be derived thus:
Fₘ = hₑ².mₚ.(ψ/R)³ {m⁴/s² . kg / m³ = kg.m/s² . m³/m³ = N}
The electrical force, which varies with temperature, may be derived as follows:
Fₘ = Ṯ.mₑ / X.Y.R {K.kg . m²/K/s² / m = kg.m/s² . K/K . m/m = N}
Where:
ψ = neutronic ratio
R = matter average atomic spacing: R = ³√[mₐ/ρ]
mₐ = atomic mass
ρ = matter density
In a perfect crystal, tensioned exactly normal to its lattice's strongest plane, it should be possible to achieve something close to its theoretical strength, which may be calculated thus:
σ = (Fₘ-Fₑ)/R²
But as stress increases, plane-slippage quickly occurs, so the actual stress must be modified to reflect shear as the atomic planes rotate, which may be calculated as follows:
σ = (Fₘ-Fₑ) . ν/R²
Young's (tensile) modulus may be calculated as follows:
E = Fₘ / R².ν³
Shear stress is the deliberate sliding of atomic planes relative to each other and therefore subject to Poisson's ratio in two planes. It may be calculated thus:
τ = (Fₘ-Fₑ) . (ν/R)²
Fabrics
Fabrics are woven matrices of organic or synthetic threads, of small diameter; ≈0.2 (≈0.008").
When calculating their (the fabrics, not the threads) strength in terms of force per unit area, we must do so using the strength of the thread.
Fabric is normally specified in terms of denier (grams) and tenacity (grams force per denier),
Strength - in terms of; e.g. N/m² - can be calculated as follows:
We begin with a datum value based upon the mass of a silk thread, 9000 metres of which has a mass of ≈1 gram.
Denier (d) is officially the mass of 9000 metres of the thread (grams).
It is actually, however, the ratio of fabric mass to 9000 metres of silk (≈1g);
If 9000 metres of fabric thread weighs 70 grams, the fabric is specified as 70 denier {70g}.
When the mass is specified as grams per denier (gpd), it has no units as it is a ratio.
When calculating the strength of the fabric in terms of N/m², we must first convert its mass to kilograms; gpd/1000
Tenacity (t) is the ultimate tensile strength of a strand of the fabric in terms of grams force {gf} per denier {gfpd or gf/g}, this value therefore, has the real units of acceleration {m/s²}.
The following conversion factor (K) nullifies the 'force' component of tenacity;
K = 9000 . g = 88259.6825124853 {m²/s²}; when applied to tenacity, the units for 't' become; m²/s²
There is no need to convert the specified tenacity value (gfpd) to kg (by dividing by 1000), because it is a ratio; g:g
Density is the measured density (ρ) of the fabric (not the thread) {kg/m³}.
The mass (m) per 9000 metres of the fabric thread is as specified; m = d/1000 {kg/m}
The cross-sectional area of the fabric strand; A = (m/9000) ÷ ρ {kg/m . m³/kg = m²}
When calculating force, tenacity (gfpd) must be converted to; m²/s² (K.t);
The breaking force; F = (K.t) . (m/9000) {m²/s² . kg/m = kg.m/s² = N}
Strength; σᵤ = F/A = (K.t).ρ {m²/s² . kg/m³ = kg.m² / s².m³ = kg.m/s² / m² = N/m²}
Example Calculation
Fabric Specification: denier; 70 {gpd}, tenacity; 23 {gfpd}, density; 600 {kg/m³}, mass; 70/1000 {kg/9000}
A = m/(ρ.9000) = 0.07 ÷ (600 x 9000) = 1.2963E-08 m²
F = (K.t).(m/9000) = (88259.6825124853 x 23) x (0.07 ÷ 9000) = 15.78867654 N
σᵤ = F/A = 15.78867654 ÷ 1.2963E-08 = 1.217984E+09 N/m²
σᵤ = (K.t).ρ = (88259.6825124853 x 23) x 600 = 1.217984E+09 N/m²
Further Reading
You will find further reading on this subject in reference publications(73)