Shaft Calculator
(critical speed and power transmission)
A shaft is a long element that is free to rotate and normally used to transfer movement or force from one end to the other. It can be any shape in section, solid or hollow and supported in bearings or bushes (Journals) in one or more positions along its length. It may also be of constant or varying size and shape along its length, and may be straight or cranked.
Two typical shaft types are shown in Fig 1. Both or either can be analysed using Shafts. Type 'b' can be analysed by addressing each section individually between any two adjacent bearings.
Fig 1. Typical Shaft Designs
Design Characteristics
When optimising the properties of a shaft it is important to concentrate on the following performance characteristics:
1) Torque capacity
2) Speed and response
3) Noise
4) Design life
By carefully optimising all four aspects you should be able to achieve a near perfect design.
Torque Capacity
The ability of a shaft to transmit high loads and yet remain responsive is due to two principal factors
a) Material: The higher a shaft's material strength, the lighter it can be. However, fatigue life must be considered as high-strength usually means brittle fracture, reducing design life (see Material Applications on this website).
b) Stress Concentrations: There should be no sharp corners or deep grooves along its length
Speed and Response
Responsiveness is always best achieved by increasing rigidity and reducing weight and drag
a) Light weight and rigidity is normally best achieved by making the shaft hollow where possible
b) Minimising drag (and therefore power transmission loss) is best achieved by accurate machining of bearing housings and selecting ball or roller bearings over journals and minimising their number. Whilst consideration should be given to fact that journals are normally capable of supporting greater lateral loads than ball or roller bearings, this is becoming less of an issue as material and machining technology improves.
Noise
Noise is always due to vibration and also a sign of potential fatigue. A perfectly balanced shaft housed in the correct bearings, properly lubricated will never vibrate as long as it is run at the correct speeds (see Vibration below). You can minimise vibration (and hence noise) by
a) Accurately balancing the shaft along its length
b) Increasing its polar moment of inertia (rigidity)
c) Running the shaft at speeds greater than 1.4 times its naural frequency
d) Accurate machining of bearing housings
Design Life
Because a shaft designed for a longer life than required will normally perform less well than one designed to fail the day after its design life expires, you should always ensure that all loading conditions have been included in your design scenario
a) Shock Load: Ensure shock loads are applied sinusoidally; i.e. not instantaneous
b) Fatigue: The more accurately you can predict the stress cycles, the more accurately you can optimise the fatigue life of your shaft
c) Wear: The better your lubrication system, the less material loss your design will need to accommodate during its operational life
The most important of the above considerations are: vibration and lubrication.
Vibration
Vibration in a rotating shaft is caused by excessive amplitudes (A). If the rotational speed (ω) of a shaft with a damping ratio of less than ≈0.7 is less than ≈1.4 times its natural frequency (ωⁿ) its amplitude will be amplified (Aƒ) greater than 1 (Fig 2), approaching infinity as it reaches natural frequency (ω/ωⁿ = 1).
The critical speed range to be avoided at all costs is 0.86 < ω/ωⁿ < 1.123, between which your shaft is likely to fail very quickly.
It is always better to aim for a running speed: ω/ωⁿ > 1.4 for a longer design life.
It is possible to install vibration absorbers in a shaft assembly, but as they normally work at a single frequency and can fail during the operational life of a shaft, they are not recommended and whilst lubrication provides some damping even the best systems are unlikely to provide a damping ratio (ζ) greater than 0.02 (see Damping Factor below). Therefore it is almost always better to reduce vibration by altering the design of your shaft. You can ensure that your shaft always runs at speeds greater than 1.4 times its natural frequency with one or both of the following design scenarios:
1) Decrease the eccentric load (W) or its CofG relative to the centreline of the shaft (e). However, these values are usually an integral part of your design and normally fixed
2) Reduce the stiffness (k) of your shaft. This can be achieved by altering the material from which it is made, its diameter(s) (Øₒ and/or Øᵢ) and/or its length, which are usually the simplest features to alter and normally provide the best results
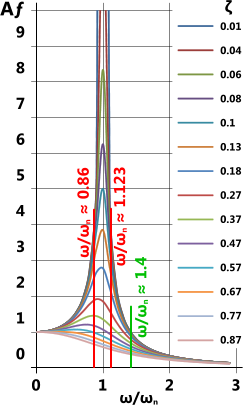
Fig 2. Damping and Amplification
Damping Factor (ζ)
The damping factor (Fig 2) is a ratio of the actual damping (C) to the critical damping (Cc) of the system defined thus: ζ = C ÷ Cc
Assuming the only reliable damping available for a shaft across its entire range of speeds is the lubricating oil, we must first assume that the oil is always present, permanently filling the clearance around the shaft⁽¹⁾.
The smaller the clearance between shaft and bush the greater the damping ratio and it is assumed that you need at least 10μm clearance to ensure free running.
Example: SAE 10 motor oil has a kinematic viscosity (ν) of 4x10ˉ⁶m²/s and a density (ρ) of 875kg/m³ and the clearance around the shaft (L⁽²⁾) is 2x10ˉ⁵m⁽³⁾ ;
C = ν.ρ ÷ L = 4x10ˉ⁶ x 875 / 2x10ˉ⁵ = 350N.s/m²
The default input data in the shaft calculator is;
W =100N, k = 3.1172x10⁷N/m and g = 9.8066m/s²;
Cc = (k.W ÷ g)½ = (3.1172x10⁷ x 100 / 9.8066)½ = 17828.84N.s/m²
ζ = C ÷ Cc = 350 / 17828.84 = 0.009816 (i.e. almost 0.01)
Refer to Fig 2 and you will see that the effect of damping from lubricating oil is negligible for this shaft⁽⁴⁾. Therefore, damping has been left out of the shaft calculator to minimise unnecessary complication. You may if you wish, however, apply a damping factor retrospectively to the results from the shaft calculator; see Applying a Damping Ratio below.
Shaft Calculator – Technical Help
Units
You may use any units you like, but you must be consistent.
Input Data
ω; the actual running speed of the shaft in revolutions per second. Shafts converts this speed to radians per second before use in its internal calculations
T; torque applied to the input side of the shaft in force per unit length. You need to match the units here with those you use for 'E'. I.e. if the units used for this value include 'g' (e.g. 'Newtons') the output stress (τ) will also include 'g'
W; weight of the eccentric mass in units of force (or weight), i.e. you must enter the mass multiplied by gravitational acceleration (g)
e; eccentricity (or off-set) of weight (W) from the centreline of the shaft. The centreline of the shaft is the straight line between the centres of adjacent bearings (one at each end of the shaft)
ℓ; distance from the specified end of the shaft to the weight (W). This is also the point at which the bending stress (σ) is calculated (see Stress Location below)
Øₒ; outside diameter of a solid or hollow shaft. The value entered should be the smallest outside diameter between the two end bearings.
Øᵢ; inside diameter of a hollow shaft. The value entered should be the inside diameter associated with Øₒ
L; the length of the shaft between the inside edges of the two end bearings
E; modulus of elasticity of the material from which the shaft has been manufactured. You need to match the units here with those you use for 'T'. I.e. if the units used for this value include 'g' (e.g. 'Newtons') the output stress (σᴾ) will also include 'g'
ρ; the density of the material from which the shaft has been manufactured
g; gravitational acceleration
Output Data
ωⁿ; resonant or natural frequency of the shaft in revolutions per second
ωʳ; ratio of 'actual' and 'resonant' (or natural) frequencies of the shaft (ω ÷ ωⁿ)
Nᶜ; critical shaft speed Nᶜ = ωⁿ x 60 in revolutions per minute
F; centrifugal force in the shaft resulting from W
yˢ; static deflection in the shaft @ ℓ as a result of W and its weight per unit length
A; amplitude in the shaft @ ℓ as a result of W rotating at ω and includes the effect of Aƒ
M; the bending moment in the shaft @ ℓ as a result of W rotating at ω
τ; shear stress induced in the shaft as a result of T
σ; bending stress induced in the shaft @ ℓ as a result of M
σᴾ; principal stress in the shaft @ ℓ due to σ and τ
k; bending spring-constant of the shaft
Aƒ; dynamic amplification factor
Dividing A by Aƒ will give you the dynamic amplification when ωʳ=0 and <1.4 (see Fig 2)
Applying a Damping Factor (ζ)
If you wish to apply a damping ratio to a calculation from Shafts for any speed (ω₀), you may do so using the following procedure:
1) Read your resultant amplification factor (ω₀/ωⁿ > Aƒ₀) from Fig 2
2) Set constant K = Aƒ₀ ÷ Aƒ
3) A₀ = A x K
4) F₀ = W x ω² x (A₀ + e) / g
5) Apply the formulas in Damping Factor (ζ) above replacing W with F₀ for your revised Cc value
6) Calculate the revised bending moment (M) and bending stress (σ) using CalQlata's Beams calculator using the correct 'Point Load' calculation option for your end conditions and applying F₀ above
7) Calculate the revised principal stress using σ and τ in CalQlata's Combined Stress calculator
Damped natural frequency: ωᵈ = ωⁿ.√(1-ζ²)
Stress Location
The bending moment (M) and consequent stresses (σ & σᴾ) in the shaft are calculated at ℓ
If you would like to know the stress anywhere else along the shaft, you can use CalQlata's Beams calculator by applying the dynamic force (F) as the point load at position 'ℓ' along the beam and entering the position 'x' for which you require a result.
Appicability
The shaft calculator is applicable to all configurations as long as each calculation refers to an unsupported length between two adjacent bearings or bushes, or a cantilever configuration (one bearing at one end of the shaft).
Accuracy
The shaft calculator is as accurate as the data entered. There is no expected margin of error. However, if a vibration absorber is fitted to the shaft, the results from Shafts will not apply to the rotational speed concerned.
Notes
- Because ball and roller bearings are normally press-fit onto shafts, this calculation generally applies to bushes (Journals) and not to roller or ball bearings
- In this calculation, L is represented by the lateral distance the shaft is able to travel through the lubrication oil
- CalQlata's Machining Tolerances calculator gives a minimum clearance of 2.0E-5m for a 30mm shaft
- The example demonstrated here is for a small shaft. Larger shafts will need larger clearances and hence reduce the dmaping ratio still further.
Further Reading
You will find further reading on this subject in reference publications(2, 3 & 4)

