Explosion Calculator
(the sudden release of energy)
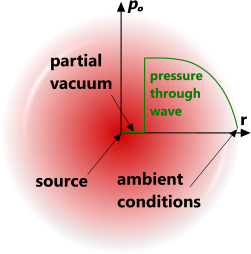
Fig 1. Explosion Pressure Wave
Explosions calculates the properties of the pressure wave resulting from a sudden release of energy in an atmosphere, the output data from which may be used to size the vents and apertures in enclosed spaces according to various standards and specifications, such as the NFPA..
Explosion (a definition)
An explosion is the sudden release of energy into an atmosphere in which it cannot be contained, and as with shock loads this can be anything from 1 Joule to many mega-Joules; it's all a matter of degree. As is the case for a pressure wave generated in an atmosphere with an energy density (pressure) greater than or close to that of the explosion (e.g. deep water) and non-existent if released into a vacuum.
Explosions can be generated from an atomic/chemical reaction or the release of a pressurised gas, both of which will result in a rapidly expanding spherical pressure wave of compressed air radiating away from the source and leaving a partial vacuum at its centre (Fig 1). This vacuum will ultimately fill with atmospheric gas when the pressure wave has lost most of its momentum.
Given that an explosion is simply the release of energy, more than one energy source exploding at the same time can be included in the final pressure wave profile by simply adding them together. The pressure from multiple explosions occurring in the same vicinity but separated by time may be superimposed but shifted according to their radial-time shift (Fig 2).
Protection
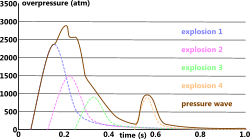
Fig 2. Multiple Explosion Profile
There are four principle threats from an explosion, each of which requires a different method of protection.
1) Overpressure
The highly localised overpressure generated by an explosion is an unnatural state for atmospheric gases (Dalton's Law), which rapidly distribute to equalise with ambient pressure and is the reason why explosion pressure waves disperse so quickly (Fig 3; overpressure).
A pressure wave generated by the release of energy within any fluid (water, air, etc.) will react against anything in its path such as an object or a barrier (e.g. container walls). Overpressure generated within a container, e.g. a room or building, can result in serious damage to its occupants from structural damage or flying objects.
Vents can be provided in enclosed spaces to prevent pressure build-up during an explosion or the risk can be moved outside behind blast-walls.
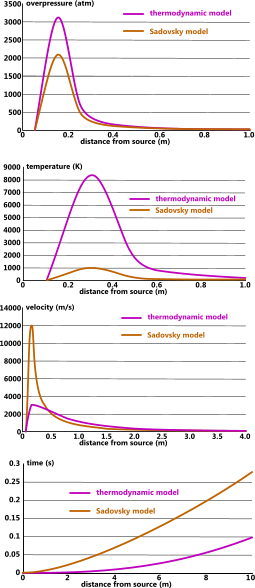
Fig 3. Typical Explosion Profiles
2) Temperature
The air pressure during an explosion is initially very high (Fig 3) and any combustible materials with a lower flash-point than the temperature generated by this pressure will of course ignite if exposed to a spark or flame. However, as can be seen in Fig 3 (temperature) this risk is highly localised.
Risk of damage from excess temperature can be avoided by moving flammable materials and substances out of the vulnerable radius. In the example shown in Fig 3 it would be necessary to move such hazards more than 1m away from the energy source.
3) Flying Objects
The overpressure generated will break and/or propel objects positioned close to the energy source. This threat is generally responsible for most of the damage/injury caused to property/personnel from an explosion.
If you know the velocity of the pressure wave on an object of mass 'm' you can calculate its launch energy from a modified version of Morison's equation;
F = ½.CD.ρ.A.v²
ρ.A = m/d (where distance 'd' = 1)
F = ½.CD.(m/1).v²
E = F.1 = ½.CD.m.v²
Insert the mass of the object (m) and the velocity of the pressure wave (v) into the fomula and you have a launch energy (E) that can be used to determine its flight trajectory along with the damage it could do to an impacted body
(see CalQlata's Engineering Principles, Velocity & Acceleration and Shock Load calculators)
Vulnerable objects should be positioned outside the high-pressure radius. In the example shown in Fig 3 (overpressure) it would be necessary to move such hazards more than 0.4m away from the energy source.
4) Ignition
The ignition of any combustible substance(s) with a flash-point below the temperature of the surrounding compressed air will release additional energy from their specific heats along with the oxygen in the air that together can significantly intensify the pressure wave as the specific heat of any substances is considerably greater than its gas constant. i.e. the energy from an explosion in a methane-rich atmosphere will rise not only according to the gas constant of air (286.8J/kg/K) but also by the specific heat of the mass of entrained methane (1964.1J/kg/K) and oxygen (659.13J/kg/K).
It is normal practice to install EX-Proof (explosion-proof) equipment close to an energy source. Such equipment will have been designed to;
a) withstand a specified explosion
and
b) isolate all means of ignition
Mathematical Models
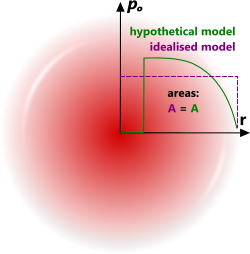
Fig 4. Thermodynamic Model
In reality the pressure, velocity and temperature profiles of the pressure wave generated by an explosion are extremely complex and vary with radial distance, elapsed time, environmental conditions and secondary effects from the proximity of obstacles, all of which interact with and affect each other. Moreover, the volume immediately surrounding the source of an explosion will become a partial vacuum due to the velocity of the radiating particles and will only refill with air after the kinetic energy of the wave front has fallen below a certain level.
Sadovsky created a mathematical model for the pressure wave generated by an explosion that has been incorporated into the explosions calculator.
CalQlata has generated a pressure wave using standard thermodynamic theory to define the behaviour of the air around an explosion, which whilst results in a similar pattern to Sadovsky's model, is more conservative in that it predicts higher pressures and temperatures but a lower velocity and faster decay due to atmospheric resistance to the pressure wave (Fig 4).
Both calculations define the properties of the pressure wave as its bow reaches discrete radial distances from the source.
The model you choose for your application should reflect the potential hazard.
(see Theories (which to choose) below).
Energy Sources
Energy sources for a typical explosion are generally physical-atomic (e.g. atomic bomb), chemical-molecular (e.g. TNT, gas cloud, etc.) or pressure (e.g. pressurised gas).
Typical chemical energy and flash-point values are provided in the table below. 'I' means that ignition will occur at any temperature when exposed to a spark or naked flame otherwise the temperature listed represents the expected minimum for this to occur:
| Substance | Chemical Formula | Energy Density (J/kg) | Flash-Point (K) |
|---|---|---|---|
| Hydrogen | H₂ | 2253209.393# | I |
| Methane | (CH₄) | 141568.056# | I |
| Methanol | (CH₃OH) | 4669840.7 | 284 |
| Acetylene | (C₂H₂) | 87224.92807# | I |
| Ethylene | (C₂H₄) | 80957.00717# | 136.6 |
| Ethane | (C₂H₆) | 75529.51059# | 138 |
| Ethanol | (C₂H₅OH) | 6111279.539 | 286 |
| Propylene | (C₃H₆) | 53971.33811# | 165 |
| Propane | (C₃H₈) | 51503.97874# | I |
| Butane | (C₄H₁₀) | 39074.56833# | 213 |
| Pentane | (C₅H₁₂) | 10095336.09 | 224 |
| Benzene | (C₆H₆) | 8704146.613 | 262 |
| Hexane | (C₆H₁₄) | 9894338.643 | 251 |
| Toluene | (C₇H₈) | 8825223.647 | 277.6 |
| Octane | (C₈H₁₈) | 9824468.101 | 286 |
| n-Decane | (C₁₀H₂₂) | 9748854.776 | 319 |
| Nitro-glycerine | (C₃H₅N₃O₉) | 1469307.951 | 543.6 |
| RDX | (C₃H₆N₆O₆) | 377370 | 533 |
| HMX | (C₄H₈N₈O₈) | 353767 | 563 |
| PETN | (C₅H₈N₄O₁₂) | 1627872.152 | 472 |
| TNT | (C₇H₅N₃O₆) | 4700000 | 440 |
| TETRYL | (C₇H₅N₅O₈) | 135507 | 460 |
| Naphthalene | (C₁₀H₈) | 8283966.235 | 352 |
| Dynamite | (SiO₂Al₂O₃Fe₂O₃ + C₃H₅N₃O₉) | 7500000 | |
| # These figures are for the associated substances in gaseous form at atmospheric pressure (1 bara) and 273K To account for temperature variations: E' = Rᵢ.Ṯ / (RAM/1000) (J/kg) To account for pressure and temperature variations: ρ = p.(RAM/1000) / Rᵢ.Ṯ (kg/m³) V = Rᵢ.Ṯ.m / (RAM/1000).p m = ρ.V (kg) E = E'.m (J) The above calculations only apply to a substance in gaseous form |
|||
Alternative energy sources:
Pressurised gas; pressure x volume {N/m² x m³ = N.m = J}
Or
Heat energy; specific heat capacity x mass x temperature {J/kg/K x kg x K = J}
where; mass = number of moles x RAM
Explosions Calculator - Technical Help
You may use any units you like for the thermodynamic model as long as you are consistent (see CalQlata's UniQon calculator). Example metric and imperial units are provided for the input and output data below.
However, the Sadovsky calculation model is based upon the metric units shown below - only.
Units
You may use any units you like in the Thermodynamic calculation option, but you must be consistent (typical units are provided in the menu item; Help>Context).
Albeit, the units for the Sadovsky model must be in the metric units recommended in the calculator menu.
Input Data:
E: energy released from the explosive or release of pressure {J} {ft.lb} #
mₑ: mass of the explosive substance; TNT, air, etc. {kg} {lb} #
ρₑ: density of the explosive substance; TNT, air, etc. {kg/m³} {lb/ft³} #
Ṯ: temperature of the surrounding atmosphere prior to the explosion {K} {R}
pₐ: pressure of the surrounding atmosphere prior to the explosion {N/m²} {lb/ft²} #
RAM: relative atomic mass of surrounding atmosphere {kg/mol} {lb/mol} #
Rᵢ: ideal gas constant {J/K/mol} {ft.lb/R/mol} #
δr: radial distance step for co-ordinate output data {m} {ft}
Output Data:
p̌: maximum pressure in wave above atmospheric [atm]
v̌: maximum velocity of the pressure wave {m/s} {ft/s}
Ť: maximum temperature due to 'p̌' {K} {R}
Rₐ: mass gas constant for atmospheric gas; air {J/K/kg} {ft.lb/R/lb} #
ρₐ: density of atmospheric gas; air {kg/m³} {lb/ft³} #
Co-Ordinates:
r: radial distance of pressure wave front from source {m} {ft}
pₒ: maximum overpressure when pressure wave front is 'r' from source [atm]
v: maximum velocity when pressure wave front is 'r' from source {m/s} {ft/s}
t: time taken for the pressure wave front to reach 'r' [s]
Ṯ: maximum temperature when pressure wave front is 'r' from source {K} {R}
K: deflagration index (NFPA 60-10; §6.1.1) at 'r' {atm.m/s} {atm.ft/s}
# You may use 'slugs' in place of 'lb' for Imperial units of mass but you must be consistent for all instances where 'lb' appear above and your results will also be in 'slugs'
Defining Energy
Explosive Substance: multiply the mass of the explosive material by its stored energy density (see Energy Sources above)
Pressure Release: multiply the volume of the pressurised gas by its pressure
The density of the pressurised gas can be determined thus: ρₐ = p / Rₐ.Ṯ; where p is the pressure of the pressurised gas, Rₐ is its mass gas constant and Ṯ is its temperature. The mass of the pressurised gas (mₑ) can then be calculated as follows: mₑ = ρₐ.V; where V is the volume of the pressurised gas.
Gas Cloud Ignition: You can determine the energy released by the ignition of, e.g. a methane gas cloud as follows:
Volume (V) = volume of room or enclosed space
mass (mₑ) can be estimated either by the percentage atmospheric content (by mass or volume 'V') or from flow rate and elapsed time
Energy (E) = mₑ x 11432926 J/kg for methane gas
Gas Constant (Rᵢ) should be replaced with cv for the same gas (based upon a constant volume process) that can be calculated as follows: cv = Rₐ x N;
where Rₐ = 518.7 J/K/kg and microstate N ≈ 3.0 for methane (pent-atomic {5 atoms}) at ambient temperature
Theories (which to choose)
As can be seen in Fig 3, the thermodynamic model is more conservative than the Sadovsky model. CalQlata therefore recommends that the thermodynamic model be adopted for very dangerous applications.
Applicability
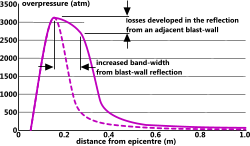
Fig 5. Effect of Blast-Wall Reflection
This calculation is applicable to the sudden release of any energy source from a mid-air location. It does not include secondary effects such as reflection forces and absorption from surrounding obstacles. If an energy source is located close to a blast-wall designed to reflect the explosion, this will have the effect of widening the pressure band away from the wall, not increasing its intensity (Fig 5).
This calculation may be used to size ventilation apertures in enclosures in which an explosion occurs.
Accuracy
Sadovsky's formula is generally expected to be relatively accurate up to 10 atmospheres, above which, its correlation with reality may be less reliable.
The thermodynamic model is based upon sound, well known and universally recognised thermodynamic principles. It does, however, assume a flat pressure gradient through the pressure wall (Fig 4; idealised model), which is unlikely. However, the idealised model is no more unlikely than any other anticipated pressure wave profile given the infinitely variable nature of an explosion. Moreover, this theory is based upon the inclusion and general distribution of all energy released with no losses. It is therefore both realistic and conservative.
Further Reading
You will find further reading on this subject in reference publications(1, 12 & 13)

