Wire Rope Calculator
Wire rope is also known by many other names, such as: wire, multi-strand wire, flexible wire, cable, cord, steelcord, etc. but it is essentially a collection of small filaments wound around each other in a manner that largely retains its shape when bent, crushed and/or tensioned.
It is a system for significantly increasing the strength and flexibility of steel wire and is used in almost every important application we see around us. For example: suspension bridges, tyres, brake and accelerator cables (in cars), high-pressure flexible pipes, lifting and rigging cables, electrical conductors, etc. and it comes in many different forms. Fig 2 shows just a very small sample of available designs.
Wire Rope Designation
With minor variations, the generally accepted method for designating a wire rope construction in the industry is by describing it numerically. For example:
'7x0.5 HT' refers to a strand of 7 filaments 0.5mm in diameter and manufactured from high-tensile steel
and
'0.43+6x0.37+6x(0.37+6x0.33) HT' refers to a seven strand construction: a single central strand (one central filament diameter 0.43mm and 6 planetary filaments of diameter 0.37mm) and 6 planetary strands (one central filament of diameter 0.37mm and 6 planetary filaments of diameter 0.33mm) all manufactured from high-tensile steel'
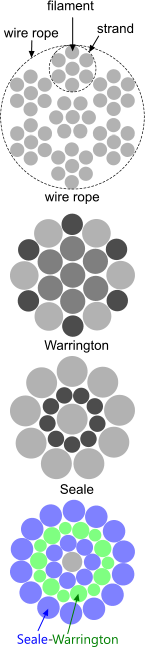
Fig 1. Basic Designs
Wire Rope Construction
Whilst 'IWRC' wire ropes offer a slightly greater tensile capacity (≈7%) than those with fabric or polymer fillers, the additional strength does not come from the tensile capacity of the core filaments but from improved dimensional stability under load. And whilst they are also much more resistant to crushing, they are stiffer than fibre core ropes and therefore not recommended for applications where tension occurs under bending.
Wire Rope (Figs 1 & 2 1x7 & 7x7) is a parallel lay construction with all filaments the same diameter and tends to be the stiffest of them all.
Warrington (Fig 1) is a parallel lay construction with an outer layer comprising wires of alternating large and small diameters, each outer layer having twice the number of wires as the layer immediately beneath. The benefit of this design is to increase packing and therefore strength density, however, unless the different diameter filaments are of the same strength (unlikely), this construction is limited by the strength of the weakest filaments.
Seale (Figs 1 & 2 6x36) is also a parallel lay construction but with the same number of wires in each wire layer. All the wires in any layer are the same diameter. This is an alternative to the Warrington construction, with similar benefits and disadvantages.
Tyrecord generally comprises a single strand of less than 1.5mm in diameter and normally contains about 12 filaments all of the same diameter between 0.15mm and 0.25mm, but designs and configurations can vary considerably dependent upon manufacturer and tyre design requirements. This design tends to be the most flexible of all constructions.
OTR is more or less a complicated tyrecord construction (see above) up to 4.5mm in diameter containing around 100 filaments of a similar size to tyrecord, albeit towards the larger end of the size range (0.2mm to 0.25mm).
Hosecord is normally a single strand Wire Rope type construction with filament diameters greater than 0.5mm.
Regular Lay vs Lang Lay
Whilst there is very little difference between the relative strengths of the two lay patterns;
Regular lay constructions are used much more widely (than Lang lay) because they have excellent structural stability and less tendency to unwrap under tension (see Rotating vs Non-Rotating below). However, because it has a knobbly (undulating) surface it will wear both itself and any surface over which it is run much more quickly than Lang lay wire rope.
Lang lay constructions have a flatter surface than regular lay constructions giving them better resistance to wear and bending fatigue, especially when made from flattened (elliptical) filaments. They are, however, much less structurally stable and subject to birdcaging if the wire rope is over-bent or twisted against its wrapped direction.
Rotating vs Non-Rotating
'Regular Lay', multi-strand constructions are normally subject to slightly less rotation under tension (than Lang lay) due to the opposite helical direction of the filaments (within the strands) and the strands (within the rope), however, you can improve their rotation characteristics still further by;
a) using fillers (see Fillers below), and/or;
b) altering the wire sizes in the inner and outer strands to optimise relative torque in each layer, and/or;
c) increasing the number of strand layers (i.e. reducing the filament and strand diameters (see Strength below)
Whilst there are very distinct non-rotating constructions such as 19x7 and rotation-resistant designs such as 19x19, new ideas are evolving all the time and each manufacturer will have its own design preferences.
'Lang lay' and single strand (e.g. Fig 2 1x7) constructions will always try to straighten (unwrap) under tension. There are a number of things that could be done to minimise this problem, such as a) to c) above and/or;
d) use less than 15% of the rope's tensile capacity, and/or;
e) wrap strands in adjacent layers in opposite directions, and/or;
f) fit a swivel to the free end

Fig 2. Designations
Fillers
Fillers (Fig 2) may be fabric, polymer or even smaller diameter filaments (e.g. 6x36). Whilst they contribute little to the tensile strength of wire rope, they can significantly; improve performance under bending (fabric and polymer cores only), reduce axial growth, reduce rotation in rotation-resistant constructions, improve structural stability and increase fatigue life.
There is little point in having a central core manufactured from the same material as the filaments as it will be the first to break. If you need a metal core, this should be of a material with lower axial stiffness than the strand that surrounds it.
This filler material should not be included in strength (tensile capacity) calculations, but must be included in those for axial stiffness (extension). If it is ignored, your calculations will reveal excessive extension as the wire rope collapses.
Wire Rope Strength
All filaments are formed from Bead Wire and further heat treated during the drawing process to achieve the high-strength filaments defined above.
The highest strength filament steels tend to be those that have been drawn-down the most, i.e. the smallest diameter.
NT (normal tensile) wire is normally greater than 0.5mm diameter and less than 1500MPa
HT (high tensile) wire is normally between 0.25 & 0.5mm diameter and between 1500MPa & 2000MPa
ST (super tensile) wire is normally between 0.1 & 0.25mm diameter and between 2000MPa & 2500MPa
The above values will vary slightly between manufacturers and specialist applications.
Wire Rope Applications
Suspension bridges tend to be constructed from densely packed, single strand plain 'Wire Rope' constructions using large diameter galvanised filaments. Little heed is paid to rotational resistance as strength is paramount and once tensioned, they should remain in that loading condition for their design life.
Lifting & winching normally require wire ropes of good flexibility and fatigue resistance. Therefore they tend to be similar to 6x36 but with fibre core instead of the IWRC in Fig 2
Hosecord is suitable for HPHT flexible pipes as lateral flexibility is generally considered less important than minimal longitudinal growth or maximum tensile strength (per unit cross-sectional area).
Remote operating cables such as hand-brakes and accelerators on cars normally only work in tension so they need to be strong but not necessarily stiff (as they are fully contained in reinforced outer sheaths). These tend to be manufactured from large diameter 'TyreCord' or small diameter single-strand 'Wire Rope'.
Axial Stiffness
Axial stiffness is the linear relationship between axial strain and force that allows us to predict the condition of any material or structure when exposed to a specified tensile force. However, it works only with materials and structures that obey Hooke's law.
Wire rope does not obey Hooke's law. Therefore, you cannot accurately predict how much it will stretch for any specified force. This unpredictability applies to any section removed from the same manufactured length of cord and even between cords produced to the same specification but by different manufacturers.
CalQlata has decided that the accuracy of axial stiffness (EA) of wire rope falls outside its own levels of acceptability and therefore does not include it in the wire rope calculator. The extension calculated in the Wire Rope calculator (δLᵀ) is based upon the effect of axial tension on packing density. It is therefore important that core material is not ignored when using the calculator to evaluate this characteristic.
See Tensile Modulus (E) below for an approximate calculation method.
Torsional Stiffness
Torsional stiffness is the linear relationship that allows us to predict the rotation of any material or structure when exposed to a torque. However, it works only with materials and structures that obey Hooke's law.
Wire rope does not obey Hooke's law. Therefore, you cannot accurately predict how much it will twist for any specified torque. This unpredictability applies to any section removed from the same manufactured length of cord and even between cords produced to the same specification but by different manufacturers.
Moreover, it is bad practice to deliberately induce twist into wire rope.
CalQlata has decided that the accuracy of torsional stiffness (GJ) of wire rope falls outside its own levels of acceptability and therefore does not include it in the wire rope calculator.
Wire Rope Calculator - Technical help
Units
You may use any units you like, but you must be consistent.
Calculation Limitations
It is important to understand the following before using any wire rope calculator:
1) No wire rope calculator, whether dedicated or generic, will accurately predict the properties of any single construction under a wide range of loading conditions
2) No wire rope calculator, whether dedicated or generic, will accurately predict any single property for a range of constructions under a wide range of loading conditions
3) Unless additional heat treatment or material modification is performed during the manufacturing (drawing) process, the smaller the filament diameter the greater will be its SMYS
4) Wire ropes containing multiple filament diameters of similar tensile modulus will only be as strong as its weakest filament(s)
5) The tensile strength of wire rope is not affected by its diameter
6) Lay patterns do not significantly affect wire rope strength
7) The many different available lay patterns are created for the following reasons:
a. Increase packing density (e.g. Seale & Warrington)
b. Improve anti-rotation properties (mixed helices)
c. Improve wear resistance (e.g. Lang lay)
d. Prevent birdcaging (e.g. regular lay)
e. Minimise limiting bend radii
f. Improve fatigue life
g. Create patentable products
8) Bending stiffness (EI) of any wire rope varies with tension and bending radius
(see Bending Stiffness below)
9) Axial stiffness (EA) varies non-linearly with tension
(see Axial Stiffness below)
10) Torsional stiffness (GJ) varies unpredictably and non-linearly with torque
11) It is not good practice to induce twist in a wire rope as this will encourage birdcaging
The only wire rope that can be reliably analysed is that which is used for suspension bridges, because; it comprises a single strand, is very densely packed, has negligible twist, contains filaments of only one diameter, is never subjected to minimum bending and every filament is individually tensioned.
There is a very good reason why manufacturers do not present calculated performance data for construction or design proposals, because even they cannot accurately predict such properties and quite rightly rely on, and publish, test data.
Calculation Philosophy
During his time working in the industry, the wire rope calculator's creator has seen, created and abandoned numerous mathematical models both simple and complex. He has gradually developed his own simplified calculation principle based upon his own experience that still provides him with consistently reliable results of reasonable accuracy.
The purpose of CalQlata's wire rope calculator is to provide its user with the ability to obtain a reasonable approximation for a generic construction, after which, accurate test data should be sought from the manufacturer for the user's preferred construction.
The calculation principle in the wire rope calculator is based upon changes in the properties of the wire rope that occur with variations in packing density under tension
Bearing in mind the above limitations CalQlata can provide the following assistance when generating (manipulating) the wire rope calculator's input data and interpreting its output
Units
There are no units specified for this calculator
Refer to How They Work
Input Data
Percent Break Load (T [%])
Tension applied to wire rope as a percentage of the break load (Fb).
Unless good reason is provided to do otherwise, core material should be ignored for these calculations.
This value should not exceed 50% for operational purposes (see Fb below)
Does not affect: Aᶠ
wire diameter (Ø)
The minimum internal diameter of a ring through which the rope can be passed in a straight line without twisting or manipulation.
Does not affect: Fb, ρˡ or Aᶠ
filament diameter (d)
If all the filaments in your wire rope have the same diameter, then you simply enter this diameter for 'd'
Alternatively, for wire rope with multiple filament diameters, you need to find an equivalent diameter with the following proviso; you must enter the minimum filament yield stress (SMYS)
Numerous methods may be used to determine an equivalent single diameter; one such is provided below:
d = √[(n₁.d₁² + n₂.d₂² + n₃.d₃² + n₄.d₄² + ...) / (n₁ + n₂ + n₃ + n₄ + ...)]
Does not affect: A
number of filaments (n)
If all the filaments in your wire rope have the same diameter, you simply enter the total number of filaments 'n'.
It is important to ensure that whilst core filaments are ignored in tensile calculations, they must be included in those for tensile extention (δLᵀ).
Alternatively, for wire rope with multiple filament diameters, you enter the total number of filaments of all diameters
n = n₁ + n₂ + n₃ + n₄ + ...
Does not affect: A
minimum yield stress (SMYS)
If all the filaments in the wire rope are of the same strength, you simply enter the SMYS of the filament material
Alternatively, for wire rope with multiple filament strengths, you must enter the minimum value
Only affects: Fb and Rᵀ
material density (ρᶠ)
It is expected that apart from fillers, all the material in the wire rope will be identical and therefore have the same density, i.e. using different materials will result in less than 'best' performance. However, if such a construction is proposed, you can calculate an equivalent density as follows:
ρᶠ = (ρ₁.d₁².n₁. + ρ₂.d₂².n₂ + ρ₃.d₃².n₃ + ρ₄.d₄².n₄ + ...) / (d₁².n₁. + d₂².n₂ + d₃².n₃ + d₄².n₄ + ...)
Only affects: ρˡ
material Young's modulus (Eᶠ)
The tensile modulus of the filament material
It is expected that apart from fillers, all the material in the wire rope will be identical and therefore have the same tensile modulus, i.e. using different materials will result in less than 'best' performance. However, if such a construction is proposed, you should enter the highest tensile modulus.
Alternatively, you can calculate an equivalent tensile modulus as follows:
Eᶠ = (E₁.d₁² + E₂.d₂² + E₃.d₃² + E₄.d₄² + ...) / (d₁² + d₂² + d₃² + d₄² + ...)
Only affects: EI, Eᵀ and Rᵀ
Output Data
break load (Fb)
The maximum load that can be sustained by the wire rope until the first filament breaks.
Refer to Input Data > number of filaments (n) above. It is highly unlikely that the applied load will be evenly distributed through all filaments.
The wire rope calculator simply adds together the total area of all the filaments and multiplies them by the SMYS entered, which represents a theoretical maximum breaking load that would exist if this load is equally shared across all of the filaments and the lay angles have been arranged to eliminate localised (point) loads between adjacent filaments.
If the wire rope has been properly constructed it is likely that its actual break load will be greater than 80% of this theoretical value. However, given the vagaries of wire rope construction, the actual break load can vary considerably dependent upon a number of factors. CalQlata suggest that the following factors may be used to define the anticipated break load of any given construction:
Manufacturing quality (fᵃ): Excellent; 0.98, Good; 0.95, Average; 0.9, Poor; 0.8
Complexity⁽¹⁾ (fᵇ): Low; 0.95, Medium; 0.9, High; 0.85
Material strength (fᶜ): NT; 0.95, HT; 0.9, ST; 0.85
The anticipated break load will be: Fb' = Fb x fᵃ x fᵇ x fᶜ
i.e. for a wire rope with a theoretical breaking load (Fb) of 10t, the first filament will be expected to break in ...
good quality/simple NT wire rope at around; 10 x 0.98 x 0.95 x 0.95 = 8.84t (±5%)
average HT wire rope; 10 x 0.9 x 0.9 x 0.9 = 7.29t (±15%)
poor quality/complex ST wire rope; 10 x 0.8 x 0.85 x 0.85 = 5.78t (±25%)
area of filaments (Aᶠ)
The sum of the cross-sectional area of all the filaments (d)
The accuracy of this data will be ±0%
linear density (ρˡ)
The mass per unit length of the wire rope at zero tension.
Accuracy is expected to be within ±0.1% of the calculated value for good quality manufacturing but variations in manufactured filament diameter can, in extreme cases, reduce this to ±1%
The linear density at tension (T) can be calculated thus: ρˡᵀ = ρˡ / (1+δLᵀ)
area of wire (A)
The cross-sectional area of the wire diameter (Ø) at zero tension
The accuracy of this data will be ±0%
The cross-sectional area at tension (T) can be calculated thus: Aᵀ = π.(Ø.(1+δØᵀ))² / 4
δØᵀ will be negative under tension, so (1+δØᵀ) is actually (1-δØᵀ)
area moment (I)
The anticipated second moment of area of the wire rope at zero tension
The accuracy of this data is expected to be ±5%
tensile modulus (E)
The anticipated tensile modulus of the wire rope at zero tension
The accuracy of this data is expected to be ±10%
This value varies with bending (see Bending Stiffness below)
packing density [%] (ρᵖ)
The percentage cross sectional area of the wire rope (A) occupied by the filaments at zero tension.
The accuracy of this data will be similar to that expected for linear density
A warning will be displayed if this value exceeds the maximum possible value:
ρᵖ ≤ ¼.π / √¾ {90.67%}
This property will have a significant effect on the behaviour of the wire rope under tension;
i.e. the lower the packing density the greater the dimensional variation (e.g. flattening, reduction in diameter, growth, etc.) that will occur.
The axial stiffness and strain under load will be affected by this value, hence the reason why the most reliable (predictable) constructions tend to be minimum [number of] strands and single filament diameter. The Warrington and Seale constructions and combinations thereof tend to provide the highest packing density (but lowest flexibility) and there is little to be gained from using these constructions in more than single stranded wire rope as the benefit of high-packing density will be lost with no gain in flexibility.
area moment @ 'T' (Iᵀ)
The anticipated second moment of area of the wire rope at tension 'T' due to deformation but insignificant flattening as it is assumed the wire rope will be bent over a formed (shaped) sheave or roller.
The accuracy of this data is expected to be ±10%
tensile modulus (Eᵀ)
The anticipated tensile modulus of the wire rope at tension 'T' due to deformation but insignificant flattening as it is assumed the wire rope will be bent over a formed (shaped) sheave or roller.
The accuracy of this data is expected to be ±10%
This value varies with bending (see Bending Stiffness below)
packing density @ 'T' [%] (ρᵖᵀ)
The percentage of the reduced cross sectional area of the wire rope occupied by the filaments at tension 'T'
The accuracy of this data is expected to be similar to the percentage change in diameter (δØᵀ)
minimum bend radius (Rᵀ)
Minimum permissible bend radius for the wire rope that will induce SMYS in the outer-most filament when coincident with the applied tension 'T'
The accuracy of this data is expected to be ±10%
It is not advisable to induce this bend radius in operation due to uncertainties associated with wire rope construction, especially for dynamic applications. CalQlata suggests that a similar approach to that used for the break load (Fb) above also be applied here, i.e.:
Rᵀ' = Rᵀ ÷ fᵃ ÷ fᵇ ÷ fᶜ
change in diameter [%] (δØᵀ)
The reduction in diameter (this value will be negative) at tension 'T'
The accuracy of this data will range between ±5% for simple constructions to ±10% for the most complex
A change in diameter will occur in all wire rope, irrespective of construction, until packing density has reached a limiting value. The value provided in the wire rope calculator is that which would be expected if the construction remains intact at the applied tension 'T'
Unreliability of this value increases with complexity in wire rope due to its longitudinal variability and the increased likelihood of premature failure.
change in length [%] (δLᵀ)
The increase in length (this value will be positive) at tension 'T'.
Refer to Input Data > number of filaments (n) above.
The accuracy of this data will range from about ±1% for wire rope with a single strand and a single filament diameter, up to about ±15% for constructions of similar complexity to OTR cord
A change in length of any wire rope will occur due to the fact that the packing density increases with tension. This is not, however, a linear relationship.
This can be an unreliable value as illustrated by tests carried out (by the author) on two pieces of wire rope supplied by the same well-known manufacturer both of which were cut from the same length, varied in tensile capacity by only 1.5%, but the tensile modulus (and strain at break) varied by 34%. Whilst this was an extreme case, significant variations have been seen in wire rope manufactured by a number of manufacturers.
Axial Stiffness
Whilst the wire rope calculator does not calculate axial stiffness (see Calculation Limitations 9) above), CalQlata can suggest the following rule-of-thumb that will provide reasonable results for most constructions at the applied tension 'T':
EA = Eᵀ . A.(1+δØᵀ)² . Cos(θ)
Where: θ = the 'absolute' sum of the average filament lay angle and the average strand lay angle⁽²⁾. Note; the angle of twist (θ) will reduce as tension approaches break load.
Bending Stiffness
Whilst the wire rope calculator does not calculate bending stiffness (see Calculation Limitations 8) above), CalQlata can suggest the following rule-of-thumb that will provide reasonable results for most constructions at the applied tension 'T':
EI = Eᵀ.Iᵀ . Rᵀ/R
Where: R = the radius of the sheave used, which must be greater than Rᵀ
Notes
- Low complexity means single strand and single wire diameter. Medium complexity means multi-strand and single wire diameter. High complexity means multi-strand and multiple wire diameters.
- If the filament lay angle and the strand lay angle are in opposite directions, as with Regular Lay constructions, you must add the angles together as positives; i.e. -12° + 23° = 35°
Further Reading
You will find further reading on this subject in reference publications(2, 3, 26 & 27)

