Vibration Damping Calculator
Vibration Damping
Resonance will occur in any undamped element that obey's Hooke's law when it is vibrated at or close to its natural frequency, and can be unpredictable. Long-term exposure to moderate levels of resonance or instantaneous exposure to excessive resonance will result in premature failure.
An element will repeatedly deform (or deflect) when subjected to cyclic loading by an amount proportional to the magnitude of the dynamic load and inversely proportional to its stiffness. The frequency of the cyclic load, along with the number of cycles, will define the element’s expected fatigue life (see CalQlata’s Fatigue calculator).
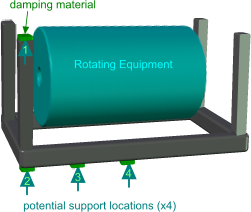
Fig 1. Typical Damped Supports
The stresses and strains induced in an element are totally predictable if it behaves exactly as expected, however, ...
when it is subjected to a cyclic load close to its natural frequency the resultant deformation will not be as expected, because at this frequency the element’s own mass and motions will influence deformation. Thus a force applied at an element’s natural frequency will generate a different deformation than would be expected from a static load (see Damping Ratio below). As can be seen in Fig 2, the amplitude magnification (Mᶠ) of an undamped (ζ=0) element operating at its natural frequency could become infinite.
Fig 1 shows the options available for positioning supports on a typical sprung system using a special material (e.g. rubber), between the mounting frame and floor or base to dampen vibrations.
Each position (1, 2, 3 and 4) will have a different natural frequency (ƒⁿ) and must be selected to avoid coinciding with the operating frequency (ƒ) of the vibrating equipment (Fig 2); see Support Positioning below. For example:
As can be seen in Shafts Fig 2, any value within the range; 0.86 < ƒ:ƒⁿ < 1.123 will be disastrous and must be avoided at all costs
As can be seen in Fig 2 below, it is also advisable to avoid any region between 0.5 < ƒ:ƒⁿ < 1.3
which is what we (at CalQlata) regard as the sensitive region
Moreover;
ƒ:ƒⁿ < 0.5 has one benefit in that transitional resonance will never occur, and one disadvantage in that amplitude magnification will normally be greater than 1
ƒ:ƒⁿ > 1.3 produces the opposite benefit and disadvatage in that transitional resonance will always occur but amplitude magnification will normally be less than 1
The choice is yours.
Damping
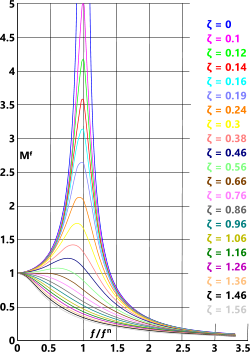
Fig 2. Amplitude Magnification Factor
Vibration damping is the reduction or avoidance of resonance and can be achieved by any of the following actions:
1) Altering the natural frequency of the sprung system (i.e. to a different frequency)
2) Altering the stiffness of the sprung system
3) Altering the location of the repeated load
4) Reducing the magnitude of the repeated load
5) Reducing the dynamic amplification of the repeated load
The normal solution to this problem (resonance) is to reduce (or dampen) the effect of the dynamically applied cyclic load by shock absorption, however, shifting the natural frequency of the element also works particularly well.
Shock Absorption: This is the slowing down of the applied load and/or its release, thereby reducing its dynamic amplification factor (see CalQlata’s Shock Load calculator) and hence the load(s) and deformation(s) in the system.
Frequency Shift: This is the altering of a system’s natural frequency away from its operating frequency (Fig 3).
Damping Methods
Mechanical Device: ... that may be adjusted during operation to modify an element's natural frequency. An example of such a design for, say, a beam (Fig 3) would be to apply a sliding mass or guide support anywhere along the beam’s length that can be repositioned during operation according to pre-defined conditions. E.g. when amplification is detected the mass/support can be slid in either direction, thereby altering its natural frequency.
These are the most complex damping methods and tend to be reserved for expensive and sensitive equipment. The more usual methods of damping, however, are the use of a special material or fluid in series or in parallel to the applied load, the reaction time(s) of which are out of phase with the system.
Material: For example, a generator operating at or close to its natural frequency that is bolted directly onto a steel frame or concrete base will fatigue earlier than expected as a result of resonance. If a material with different elastic properties (to the support, e.g. rubber pads; Fig 3) is inserted between the generator support frame and the base, the system’s natural frequency can be shifted away from the operational frequency. This method only works, however, if the material thickness is sufficient to allow at least twice the anticipated static deflection without inducing limiting tension or compression.
Fluid: For example, the use of a shock absorber instead of the material mentioned above. A shock absorber normally comprises two sealed cylinders that move relative to each other or a dash-pot with internal piston, both of which force entrained fluid to pass between the cylinders or the piston and cylinder. The viscosity of the fluid defines the rate of movement (see Viscous Damping below).
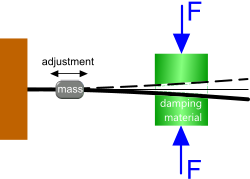
Fig 3. Mechanically Damped System
Damping Ratio (ζ)
This is the ratio of operational damping to critical damping (ζ = C:Cc) (Fig 2)
A system that is ...
overdamped; ζ > 1.0
fully damped; ζ = 1.0
underdamped; ζ < 1.0
Magnification Factor (Mᶠ)
The plot in Fig 2 shows the magnification factor expected at various frequencies and damping ratios. As can be seen in this plot, it is usually preferable to design a system that operates at a frequency greater than 1.4 times its natural frequency, as this actually generates smaller deflections than would be expected for a static load of the same magnitude.
It is also important to ensure that the operating frequency is never maintained (for more than a transient period) between 0.5 and 1.3 times the natural frequency unless the damping ratio is greater than 0.35, thereby ensuring that deflections will be kept below twice the expected static amplitude.
The possibility of reduced fatigue life must be established for all magification factors greater than 1.0
Damping Calculator – Technical Help
Units
You may use any units you like, but you must be consistent.
It is important to remember, however, that if your force values (k, F & W) include gravitational acceleration (g), e.g. Newtons or slugs, you will need to enter a correct value for gravitational acceleration (g)
If on the other hand your force values do not include gravitational acceleration, e.g. kilograms and pounds, you must set 'g' equal to 1.0
Support Positioning
A typical calculation is provided below for a damping ratio (ζ) of 0.5 that would be performed after you have designed your support frame for the required strength.
Assume the support frame is manufactured from structural members all of which have a length of 1.0, a second moment of area of 1.22656E-07 and Young's modulus of 2.07E+11;
where should you position your supports if the equipment vibrates at 45Hz (cycles per second)?
Calculate the spring coefficient (k) and natural frequency (ƒⁿ) for each position (e.g. using CalQlata's spring coefficient calculator), all of which are shown below for each distance 'ℓ' from any corner of the frame
| Position (Fig 1) | ℓ | k | ƒⁿ | ƒᵒ:ƒⁿ | Mᶠ |
|---|---|---|---|---|---|
| 1 (top of column) | 1 | 3.88E+08 | 253.5 | 0.18 | 1.02 |
| 2 (corner) | 0 | 7.64E+13 | 112480 | 0.0004 | 1 |
| 3 (¼-beam) | 0.25 | 1.156E+07 | 43.74 | 1.03 | 0.845 |
| 4 (mid-beam) | 0.5 | 4.875E+06 | 28.41 | 1.584 | 0.365 |
Position 1: according to Fig 2, this is outside the sensitive area and transition resonance will not occur if the equipment never exceeds 45Hz. However, the dynamic amplitude (Mᶠ) will be greater than the static deflection.
Position 2: according to Fig 2, this is well away from the sensitive area, transition resonance will not occur if the equipment never exceeds 45Hz and the dynamic amplitude (Mᶠ) will be no greater than the static deflection.
Position 3: according to Fig 2, this is well within the sensitive area and must be avoided.
Consideration should be given to the possibility of damping material deterioration during design life that would reduce ζ with obvious conseqences (Fig 2)
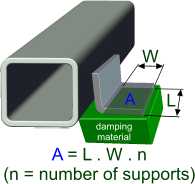
Fig 4. Damped Spacer
Position 4: according to Fig 2, this is away from the sensitive area but transient resonance will occur during start-up and shut-down. However, the dynamic amplitude (Mᶠ) will be much smaller than the static deflection, which means lower stresses, reduced fatigue and less damping material.
Input Data
k = stiffness, spring constant or spring coefficient, which is the load required to deform or deflect the system or element by one unit-length (1.0)
F = the operational cyclic force applied to the damping material E, the units of which must be same as the force component of k
ƒᵒ = the operating frequency of the applied load (F)
ζ = damping ratio, i.e. the ratio of operational damping (C) to critical damping (Cc); see Fig 2
e = the maximum permissible strain in the damping material over the cross-sectional area (A)
E = the tensile modulus of the damping material proposed for the supports
W = the total weight supported by A
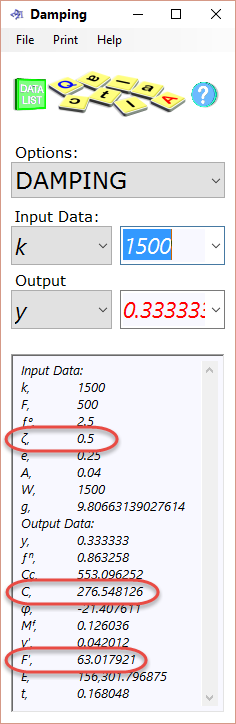
Fig 5. Damping Calculation
g = gravitational acceleration
If the force component of input data (k, F & W) includes gravitational acceleration (e.g. Newtons or slugs), this value should be entered accordingly (e.g. 9.80665, 32.174, etc.)
If the force component does not include gravitational acceleration (e.g. kilograms and pounds), this value should be set to 1.0
Output Data
y = the deflection expected in the system (k) as a result of force F applied statically
ƒⁿ = the natural frequency of the system (k) [per second]
Cc = critical damping of the system
C = operational damping of the system
φ = the phase angle or shift between the applied cyclic force (F) and the dynamic force (F′) [°]
Mᶠ = amplitude magnification factor of the static deflection or deformation (y)
y′ = dynamic amplitude of the deflection (y) due to the amplitude magnification factor (Mᶠ)
F′ = dynamic force due to ƒᵒ, which includes the momentum in the system
A = the total cross-sectional area of the damping material used for your supports (Fig 4). If you are calculating one support at a time, you need to factor (reduce) F and W accordingly
t = the minimum thickness of the damping material (E) that will ensure that the maximum permissible strain (e) is not exceeded
Viscous Damping
'Viscous damping' is the resistance to movement within a fluid of a given dynamic viscosity (dynamic shear stress), the units of which are, e.g.; N.s/m² (lb/s/ft).
The damping ratio (ζ) generated in a shock-absorber such as a dash pot, is due to the ratio of the surface area (A) of the moving part that is in contact with the fluid, e.g. a piston wall and the radial gap (h) between it and its cyliner; C/μ = A/h⁽¹⁾
Calculation Example
The required radial gap (h) between each piston and its cylinder in four dash pots similar to that shown in Fig 6, which are used to damp the system described in Fig 5, may be found as follows:
Where:
C = operating damping coefficient
μ = fluid dynamic viscosity
A = piston (wall) surface area⁽²⁾
h = radial gap between piston and cylinder
F′ = damped force (on all four dash pots)
n = number of supports (dash pots)
for a fluid of viscosity; 1.2 N.s/m², a piston of diameter 0.05m and 0.2m long
find the radial gap (h) required to generate; ζ = 0.5
A = π.Ø.L.n = π x 0.05 x 0.2 x 4 = 0.1257 {m²}
h = A.μ/C = 0.1257 x 1.2 ÷ 276.55 = 0.000545 {m}
i.e. 0.5 mm {0.02 ins}
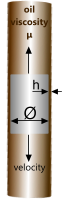
Fig 6. Dash Pot
The velocity (v) of the piston in the fluid is:
v = F′/C = 63.018 ÷ 276.55 = 0.2279 {m/s}
In the above system, you would use the four dash pots described above along with four springs that together have a stiffness (k) of 1500N/m and capable of supporting a weight (W) of 1500N but with sufficient remaining flexibility to deflect > ±0.042012 (y′)
Applicability
The vibration damping calculator applies to any system or element with a stiffness of 'k', irrespective of design, type or material.
Accuracy
The accuracy of Damping is limited only by the data entered. I.e. it is expected that if the data entered is 100% accurate, then so will be the output data
Notes
- This relationship only works if the velocity profile through the radial gap (h) is linearly variable, which can be assumed for small gaps (relative to the viscosity) but not large gaps (depths)
- The ends of the piston can be ignored as the gap between them and the cylinder are significantly greater than 'h' and therefore do not apply to the formula
Further Reading
You will find further reading on this subject in reference publications(1, 2 & 3)

