Co-ordinate Calculator (longitude & latitude)
Co-ordinates are utilised to pinpoint a location either on a 2-D surface (map) or within a 3-D volume (vector) using angles and/or linear dimensions of longitude and latitude.
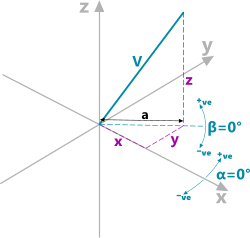
Fig 1. Vector Co-ordinate Diagram
Vector Co-Ordinates
A vector (Fig 1; V) is a quantity with both magnitude and direction that can be defined using three related dimensions, either linear or angular.
Cartesian Co-Ordinates
Cartesian co-ordinates (Fig 1), are the linear dimensions (x,y,z) that define the end of a vector with respect to two or three-dimensional axes.
Polar Co-Ordinates
Polar co-ordinates (Fig 1) define a vector with respect to a two or three-dimensional plot using angular rotations (α,β) along with its length (V).
Map Co-Ordinates
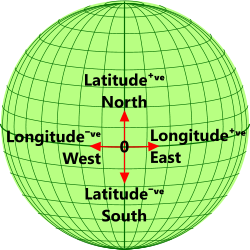
Fig 2. Map Co-ordinate Diagram
Grid co-ordinates (Fig 2) are normally used to specify a point on a map that may be a flat (2-D) plane or the surface of a 3-D volume, such as the spherical surface of a planet.
Location of a point on a spherical surface, e.g. that of a planet, can be defined either from two related angles at right-angles to each other, that are generally referred to as latitude and longitude, or from circumferential distances at right-angles to each other; e.g. the UTM system.
Co-ordinates Calculator - Technical Help
Units
You may use any units you like, but you must be consistent.
Input Data
Cartesian to Polar & Polar to Cartesian calculation options:
x, y, z: 3-D linear dimension from the co-ordinate origin to the end of the vector
V: the length of the vector
β: the vertical angle from the x,y plane at z=0 [°]
α: the horizontal angle from the x,z plane at y=0 [°]
Angle to Distance & Distance to Angle calculation options:
R: the radius of the sphere (or planet)
Lat: Latitudinal angle up (+ve) or down (-ve) from the equator [°]
Long: Longitudinal angle east (+ve) or west (-ve) from a datum vertical co-ordinate (e.g. GMT) [°]
N/S: vertical circumferential distance up (+ve) or down (-ve) from the equator
E/W: horizontal circumferential distance east (+ve) or west (-ve) from a datum vertical co-ordinate (e.g. GMT)
Output Data
... input data above and:
a: horizontal 3-D linear dimension from the co-ordinate origin to the end of the vector (Fig 1)
E/W defines the horizontal circumferential length from the datum/origin at the latitudinal height above the equator or horizontal circumferential datum. In other words, this length will reduce as the latitude (Lat) rises until at the top or bottom poles at which point Lat = 90° and E/W = 0
Applicability
The co-ordinates calculator applies to any vector length and spherical diameter within the numerical limits of the operational computer
Accuracy
The co-ordinate calculator produces no known errors.
Further Reading
You will find further reading on this subject in reference publications(15)

