Circular Plate Deflection Calculator

A plate is generally regarded as a metal block with similar face dimensions (length, breadth, circular, etc.) the shortest dimension of which is at least ten times its thickness. That said, Plates is equally applicable to those of greater thickness as deflection due to shear is included in the calculations.

The calculations included in Plates are primarily intended for the evaluation of diaphragms, membranes, caps and venturi plates associated with pipes, tubes and structures but can be equally applied to 'burst-disks' and in fact any uniformly loaded plate with annulus supports.

Whilst CalQlata's 'Sheets' calculator addresses non-circular plates and sheets, it is possible to use 'Plates' to obtain approximate results local to the loading condition for non-circular plates. However, the loaded area must be sufficiently distant from the edges of the plate to avoid edge effects. The further the loading from the edges, the closer the approximation.

Strength and Rigidity

As with CalQlata's Beams calculator, the strength of a plate is dependent upon the yield stress of the material from which it is manufactured, thereby defining the maximum load that may be applied before it will permanently deform (or break if brittle), and....

its rigidity is dependent upon its thickness along with the Young's modulus of its material, thereby defining the expected deflection in the plate for any given load

Both the above characteristics will define the behaviour of a plate under load. Refer to Applicability below

Supports

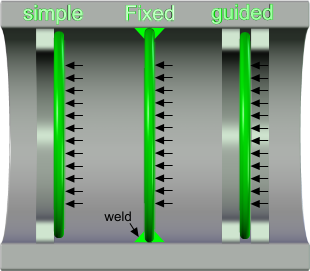
Fig 1. Various Support Options

Fig 1 shows principal support types. Refer to our Definitions page on this website for a description of each.

Design

When designing a plate for a particular application, you need to define your limiting criteria, e.g.:
1) strength or maximum allowable stress
or
2) rigidity or maximum permissible deflection

You simply alter the material and/or the thickness of your plate and recalculate until you have achieved your strength and rigidity limits, not forgetting of course to add your corrosion allowance (where necessary) to your final plate thickness.

Plate Deflection Calculator - Technical Help

Units

As with all CalQlata's programs, unless otherwise stated, you get out what you put in.
For example:
If you enter a force (F) in lbs and the radii and diameters (r and Ø) in inches, you should enter the Young's modulus (E) in the same units (lbf/in²) and all your output data will be in the same units.

Combined Stress

Plates provides you with two tensile stress results (tangential and radial) and a circumferential shear at three locations: outside edge, inside edge and your designated radius.

These stresses can be combined using CalQlata's Combined Stress calculator.

Multiple / Simultaneous Loading Conditions

Should you have a plate with more than one applied load you simply add the results together at your specified location as described in the example below:

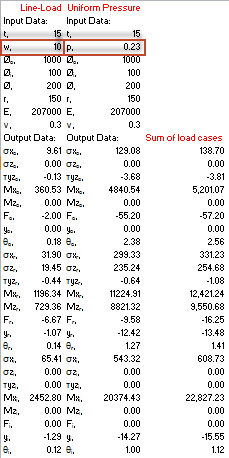
Fig 2. Multiple Loading Conditions

Plate Deflection Calculation Example:

Apply the following loading conditions:
1) circular line load (w) of 10/unit length @ Ø: 200
2) annular pressure (p) of 0.23 @ Ø: 200
... to a flat round steel ring, simply supported at its outside diameter and unsupported at its inside diameter, with the following dimensional and material properties:
  Outside diameter (Øₒ): 1000
  Inside diameter (Øᵢ): 100
  Thickness (t): 15
  Young's modulus for the material (E): 207000
  Poisson's ratio for the material (ν): 0.3

Step 1:
Enter input data for Loading Condition 1 (Simple-Free Line-Load Ring) as shown in Fig 2 and copy and paste all data into your spreadsheet

Step 2:
Enter input data for Loading Condition 2 (Simple-Free Uniform Pressure Ring) as shown in Fig 2 and copy and paste all data into your spreadsheet

Step 3:
Add results from both calculations in your spreadsheet

Applicability

As with CalQlata's Beams calculator, Plates only applies to homogeneous materials that obey Hooke's law and plates of constant thickness that retain their principal dimensions during and after deformation.

Therefore, the results obtained where stresses exceed yield for the material and/or deflections are greater than about 10% of the outside diameter will be approximate, and the greater the excess, the greater the approximation.

Further Reading

You will find further reading on this subject in reference publications^{(4 & 20)}