Thermal Insulation and Conductivity Calculator
(heat flow)
Thermal insulation is the reduction in heat loss from one side of a barrier to another. The properties of the material used for the insulation layer(s) will define the rate at which internal heat is lost. The four properties that describe a barrier's thermal characteristics are all described below.
Thermal Conductivity (k)
Thermal conductivity applies equally well to a gas, a liquid and a solid, all of which have their own characteristic value (e.g. the thermal conductivity of water is 0.591 W/m/K (0.341 Btu/h/ft/R)).
Specifically, it is the quantity of heat (British Thermal Units or Calories) that passes through a barrier of unit thickness (1.0 foot or metre) separating a unit temperature difference (1.0 Rankine or Kelvin) over a unit period of time (1.0 second, minute or hour). The units used to describe this property can be in numerous forms mixing various units of length, but are normally expressed in Imperial units as "Btu/h/ft/R" and in metric units as "W/m/K".
Refer to 'Applicability' below
Heat Transfer Rate (q)
Heat transfer rate applies equally well to a gas, a liquid and a solid and refers to the rate at which a volume of it will lose its heat to its surroundings.
Specifically, it is the quantity of heat (British Thermal Units or Calories) that passes from a material or substance in a unit period of time (1.0 second, minute or hour). The units used to describe this property can be in numerous forms, but are normally expressed in Imperial units as "Btu/h" and in metric units as "W".
Refer to 'Applicability' below
Heat Transfer Coefficient (U & h)
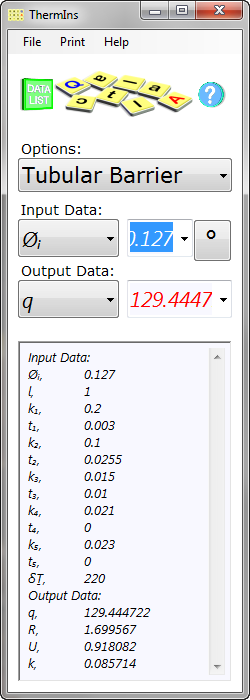
Fig 1. Heat Loss from water
Heat transfer coefficient applies equally well to a gas, a liquid and a solid but is normally used as the thermal property specification for commercial products such as insulation boards or materials of a given thickness. So if you multiply this value by the thickness of the barrier material, you will have the Thermal Conductivity of the material from which the barrier has been manufactured.
Specifically, it is the quantity of heat (British Thermal Units or Calories) that passes through a barrier separating a unit temperature difference (1.0 Rankine or Kelvin) over a unit period of time (1.0 second, minute or hour). The units used to describe this property are normally expressed in Imperial form as "Btu/h/ft²/R" or in metric form as "W/m²/K".
Refer to 'Applicability' below
Thermal Resistance (R)
Thermal resistance applies equally well to a gas, a liquid and a solid and describes the ability of the material to prevent heat loss.
Specifically, it is the temperature difference (Rankine or Kelvin) across a barrier when a unit rate of heat (British Thermal Units per hour or Watt) is passed through it for a unit period of time (1.0 second, minute or hour). The units used to describe this property are normally expressed in Imperial form as "R/(Btu/h)" or in metric form as "K/W".
The reciprocal of thermal resistance (1/R) is thermal conductance (W/K).
Refer to 'Applicability' below
Heat Loss
This is what you do to find out how quickly differing temperatures across a barrier will equalise:
1) Multiply the volume (m³) of high-temperature substance by its density (kg/m³)
2) Multiply the result by its specific heat capacity (W.h/kg/K)
3) Divide the result by the barrier's surface area (m²)
4) Divide the result by its Heat transfer coefficient or Thermal Conductance (W/m²/K)
The units will cancel out as follows: (m³.kg.W.h.m².K) / (kg.m³.K.m².W) leaving you with 'h'(hours)
If you want to try it with water (cp = 1.163 W.h/kg/K, ρ = 1000 kg/m³) in a one metre long pipe; determine the mean surface area of your pipe and the volume of water inside it:
(Area = l.π.Øm = 0.52 m² and Volume = l.π.ز/4 = 0.012668 m³)
note: Øm is the diameter of the middle of the pipe wall thickness (including insulation)
and using ThermIns calculate the Heat Transfer Coefficient (Fig 1):
1) 1000 x 0.012668 = 12.668 kg
2) 1.163 x 12.668 = 14.73252 W.h/K
3) 14.73252 ÷ 0.52 = 28.33539 W.h/K/m²
4) 28.33539 ÷ 0.918082 = 30.86 hours
ThermIns does not include the above calculation facility because it would make the program more complicated to use and imply an accuracy that isn't true. For example, such a calculation would need to assume that the ….
1) surrounding area does not heat up as a result of the heat transmission
2) container is manufactured perfectly
3) materials are 100% homogeneous
4) sides are all made of the same materials
5) container is not in contact with any other surface
6) the heat source is not replenished
etc.
Few, if any, of which would be accurate.
Whilst CalQlata plans to release a more comprehensive thermal conductivity calculator in the future, Thermins can provide you with sufficient information to design a pipe, a barrier or container with suitable confidence and accuracy.
Thermal Conductivity Calculator - Technical Help
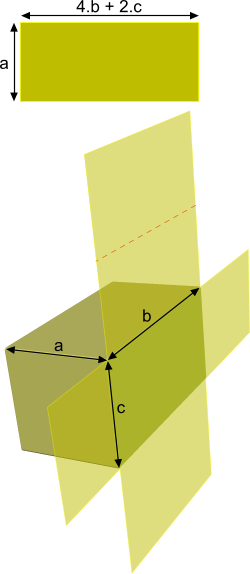
Fig 2. Container Calculations
Units
You may use any units you like, but you must be consistent.
Typical units are provided (for example only) in the Help>Context menu.
You may enter negative or positive temperature variations in the thermal conductivity calculator and both will give you similar results in the Flat Barrier calculation example, but you will notice significant differences in the results you will get for switching polarity in the Tubular Barrier calculation option. This is due to the fact that the surface areas inside and outside are different and as temperature always travels from hot to cold, the flow rates will be different into or out of the pipe.
Containers
If you want to calculate the thermal properties of a six-sided container, simply open it up and treat it like a flat barrier (see Fig 2). The results will be very close to the real thing in most cases.
There is of course an area variation due to the thickness across the corners but unless the wall thicknesses are large compared to the size of the box, the error will be minimal.
Applicability
All of the formulas in the thermal conductivity calculator are based upon linear transmission rates through all materials and all insulation layers are 100% in contact with their adjacent layers. Any variations from the above will not reflect real-life situations, however, unless the variations are significant these errors will be minimal.
Further Reading
You will find further reading on this subject in reference publications(2, 3 & 12)

