Column Buckling Calculator (Resistance)
Euler & Rankine

Fig 1.
Column
Buckling
Columns are either long and slender or short and fat and are used to support axial compression loads. If an evenly spread, (over its cross-section) perfectly parallel (with its strong axis; Fig 2) axial load is applied to a perfectly straight column of constant cross-section and made from homogeneous material throughout, the column would only deform axially under compression and its ultimate load carrying capacity would be defined by the ultimate compressive strength of the material from which it is made. However, this is never the case
Columns are never perfectly manufactured and always subjected to non-exact loading conditions. As such, whilst all columns will initially compress, they always deform laterally (column buckling) long before yield stress is reached. A bending moment (M; Fig 1) will occur in the column immediately it buckles and this bending moment will define the failure load, or buckling resistance, for the column.
In very slender columns (spars, etc.) it is most likely that column buckling will occur long before it has achieved any significant longitudinal compression. The maximum permissible loads in such columns will be significantly lower than in shorter, fatter columns.
A column's slenderness is defined by its 'Slenderness Ratio' (l/ɍ); its length divided by its least radius of gyration.
The two predominant calculation methods for these columns are:
Rankine (and Gordon), whose formulas apply to short fat columns (where l/ɍ ≤ 100) that will compress longitudinally before column buckling and eventual elastic failure occurs. This calculation method normally applies to columns used in buildings and similar constructions.
and
Euler, whose formula applies to long slender columns (where l/ɍ > 100) that will fail almost entirely through elastic lateral deformation and is normally used for aircraft spars and similar lightweight structural members.
Fixed Ends
A fixed end means a welded or riveted end but can also apply to bolted ends where the bolts are sufficiently pre-tensioned to prevent any significant elastic strain.
Pinned Ends
A pinned end means a hinged or loosely bolted, rounded or pointed end where the end of the column can rotate and deform longitudinally under load.
Free Ends
A free end is free to move in any plane and direction, resistance to which comes entirely from within the materials Young's modulus.
Column Buckling Calculator - Technical Help
The column buckling calculator provides Rankine and Euler loads for all calculations irrespective of the slenderness ratio. We do this in order to allow you to decide on the most appropriate acceptable loading condition for your column and because the decision making process is not always obvious (see Which to choose? below).
Rankine
As described above, the Rankine formula is used to determine allowable (Qᴿ) and ultimate (Pᴿ) column buckling loads that include the effects of compressive stresses. For this reason Rankine developed a safety factor (SFᴿ) that can be applied to his formula (it does not apply to Euler's formula). You will notice that with very large slenderness ratios, this value will become negative. Long before this occurs (SFᴿ<0), however, you should have adopted Euler's formula.
Euler
Euler's formula defines the geometry of the column under load and therefore results in a more conservative ultimate load (Pᴱ) than Rankine's formula. As such, this result should be used for columns of a slenderness ratio greater than Rankine's. Euler's formula is normally used for very slender lightweight columns such as those used for aircraft spars, and due to its conservative nature you can apply much lower safety factors (e.g. between 1.0 and 1.2). The column buckling calculator does not apply a safety factor to this formula, it leaves it up to you to apply your own. Having sized your 'Euler' column, you should divide the ultimate load by your preferred safety factor in order to find its maximum allowable load.
Which to choose?
CalQlata would advise the following approach to the selection process:
l/ɍ ≤ 80: always use Rankine
80 < l/ɍ < 120
1) Eccentric or non-parallel applied load – Rankine
2) Dire consequences of failure – Rankine
3) Load relaxes after deformation – Euler
4) Secondary structural element – Euler
5) Light weight requirement – Euler
6) Otherwise – Rankine
l/ɍ ≥ 120: always use Euler
Eccentric Loads
Eccentric loads are those applied 'off-center' (see Fig 2) and should be applied only to Rankine columns. Euler columns are unsuitable for eccentric loads.
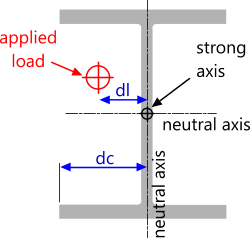
Fig 2. Eccentrically Loaded Columns
You should define your eccentricity input data as follows:
dl (distance from neutral axis to load): the perpendicular distance from the neutral axis of the weakest second moment of area to the applied load
dc (distance from neutral axis to compression side): the perpendicular distance from the neutral axis of the weakest second moment of area to the edge of the section
You can define the structural properties of your column using CalQlata's Steel Sections or Area Moments programs.
Units
You may use any units you like, but you must be consistent.
Input Data
There is sufficient information in the column buckling calculator's 'Technical>Help' page for you to perform most typical calculations.
Output Data
Columns will let you know if an obvious error has occurred. If, however, you get 'NaN' or 'infinity' you should check for incorrect input data or unacceptable zeros.
Further Reading
You will find further reading on this subject in reference publications(2)

