Buoyancy Calculator (air and water)
As Archimedes once said:
"a body partly or fully immersed in a fluid will lose the same weight as the weight of the water it displaces"# (although he probably said it in Greek!).
# We've seen statements claiming 'mass' is lost and not 'weight'. However, mass is the same for any given body anywhere in the universe, it cannot be lost unless you physically remove it
What this statement means, is that if an object is less dense than the surrounding fluid, it will float. If it is denser, it will sink. The loss of weight is not real, it is 'apparent'. The displaced fluid exerts an upward reaction on the body equal to the displaced weight of the fluid, which is the buoyancy force.
There is an alternative outcome, however. Where the densities change with depth or altitude (e.g. in the ocean or the air) the relative densities may equalise 'at depth' as a body rises or sinks.
This equalisation occurs as a result of one or both of the following two events:
1) The density (and therefore pressure) of the fluid increases faster than the body with depth
2) The volume of a body will vary with external pressure, thereby altering its density
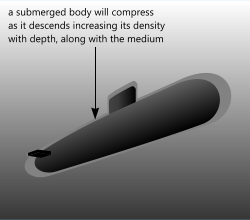
Fig 1. Buoyancy in Liquid
When the buoyancy calculator refers to 'effective density', it means 'the total mass of the object (including structure and cargo) divided by the volume it displaces'
Submarines
A submarine works by adjusting its total mass (hull plus content) to the same mass of the water it displaces at a given depth and it does this by pumping seawater in or out of its ballast tanks.
The decrease in a body's volume and the increase in a fluid's density due to increased pressure are the things nautical engineers use to design submarines. The effective density can be altered by pumping water (ballast) into and out of the submarine's ballast tanks causing it to rise and fall within the water column. A submarine is designed such that if all of its ballast tanks are emptied its effective density is less than seawater at the surface, so it will float, partially submerged, on the surface.
Care must be taken not to over-fill its ballast tanks, however, as doing so could cause the submarine to sink to a depth whereby its outer casing (the submarine's hull) will be unable to support the pressure of the surrounding water. The casing will collapse, reducing the volume permanently and dramatically such that it will be impossible to equalise internal and external densities. The submarine will then simply continue to sink until it sits on the ocean floor.
AirShips (and structural blimps)
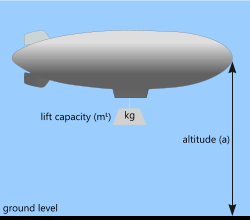
Fig 2. Low Density Gas (large)
The same buoyancy force applies to bodies immersed in a gas. For example, airships (or blimps) are essentially large [predominantly] cylindrical balloons filled with a gas significantly less dense than the surrounding air (e.g. helium or hydrogen). If the composite density of the airship and the gas it contains is less that the density of air it displaces, the airship will be buoyant in air. Whilst hydrogen offers about twice the lift capacity of helium
(ρ: He = 0.177kg/m³, H = 0.08987kg/m³)
it is highly combustible when mixed with the oxygen in air (i.e. the Hindenburg) and is therefore rarely used in passenger carrying airships.
Given that air pressure (and hence its density) drops with altitude (see also CalQlata's UniQon calculator), whilst an airship may be sufficiently light on the ground to initiate lift, it will only rise until its own effective density is equal to that of the surrounding air.
In order to maintain height during flight in the event of gas leaks, on-board tanks of highly pressurised helium or hydrogen are used to maintain a positive internal pressure of the lighter gas. Otherwise, the balloon will become heavier as air replaces the lighter gas via the leaks.
In order to fly an airship at the correct height, it is essential to balance all weights (construction and cargo). Overloading an airship will cause it to achieve a lower than predicted altitude.
Helium-Filled Balloons
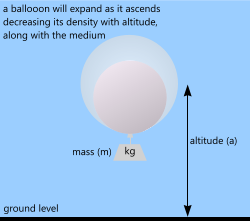
Fig 3. Low Density Gas (small)
A spherical helium-filled balloon can be any size or capacity and may be tethered (to the ground) to maintain height and position or left to float free at a predetermined altitude.
Unlike airships (see above) the volume of an elastic-membrane balloon increases with altitude, reducing its density accordingly.
If you continue to pressurise a non-structural, elastic membrane (balloon) with a low density gas (e.g. helium or hydrogen) until its effective density is less than the surrounding air (on the ground) it will rise and as it does so its volume will increase until one of two things occur:
1) The membrane stretches to a point where it has exceeded its ultimate tensile strength and the balloon bursts, or
2) Its effective density is equal to the surrounding air and it will hover at that altitude without rising any further
Helium-filled balloons are normally (but not always) small (< 3m diameter) spherical polymer membranes used to carry instruments to a predefined altitude. This altitude can be maintained in one of two ways:
1) The balloon can be tethered to the ground using a fixed length tether, or
2) A balloon and its cargo can be carefully sized to ensure that it hovers before it bursts
If the balloon is to be tethered to the ground, it will need to be significantly larger than 3m in order to provide sufficient buoyancy force to carry the weight of the tether, but the advantage is that the balloon stays in (relatively) the same place whilst operational and it can be easily recovered.
Hot-Air Balloons
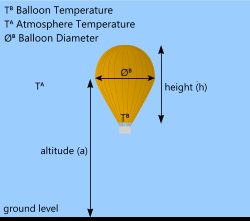
Fig 4. Hot-Air Lift
A hot air balloon is slightly different from the two previous designs in that it is not filled with a special gas and it is not a closed structure. Hot air balloons rely on heating the air trapped inside an open envelope (the balloon) until its density is low enough to provide sufficient buoyancy force for it to float upwards. The air is normally heated to about 97°C.
As the balloon rises, however, it does not expand so its density changes only as a result of the heated air (≈ -20%). Therefore, just like an airship, it will rise until the effective density is equal to the surrounding air, at which point the balloon will hover and rise no further. At this point the buoyancy force is equal to the total weight of the balloon.
As the air in the balloon loses heat through the envelope material (formerly silk but normally 'Ripstop' nylon today) it is reheated by igniting the burner for short bursts. After you have run out of burner fuel you can either keep floating until the temperature drops to that of the surrounding air during which time the balloon will continue to lose height, or you can open flaps in the envelope releasing hot air and increasing the balloon's effective density.
Buoyancy Calculator - Technical Help
Liquid
As most submerged objects are composites (e.g. a submarine), you are asked to enter a displaced volume (Vd) and a body mass (mo). Buoyancy will convert these into an effective density. If the submarine casing is made from steel, you can input the compressibility (ko) for steel to represent the object.
The compressibility (ko & km) of solids and liquids are very small and minor variations can cause a fixed body mass floating mid-water to rise or sink. In order to cause a body to float mid-water in the buoyancy calculator you should first set the densities equal where buoyancy (b) is zero (0), displacement volume (Vd) is equal to the object volume (vo) and depth (d) is zero (0). Then slightly increase the object mass (mo) to see how far it sinks. A steel body in seawater will need to be only about 0.1% denser than the seawater to float mid-depth. Try this one for instance:
| Input Data: | |
| object volume (Vo) | 100 {m³} |
| object mass (mo) | 102600 {kg} |
| object compressibility (ko) | 7.0412E-11 {m²/N} |
| liquid volume (Vm) | 50000000 {m³} |
| liquid density (ρm) | 1025 {kg/m³} |
| liquid compressibility (km) | 4.13468E-09 {m²/N} |
| liquid depth (dm) | 1000 {m} |
| atmospheric pressure (atm) | 101325 {N/m²} |
| gravitational acceleration (g) | 9.81 {m/s²} |
| Output Data: | |
| buoyancy (b) | -100 {kg} buoyancy force on the submarine |
| displaced volume (Vd) | 99.99686 {m³} |
| settle depth (d) | 671.79177 {m} |
| liquid depth increase (δdm) | 0.002 {m} |
| density at d (ρ) | 1,026.032219 {kg/m³} |
The liquid volume ('Vm') is included to enable you to determine the increase in depth (rise in surface level) as a result of immersing the object. For example, if you set Vm to 3.4E+17 (the approximate volume in m³ of the earth's oceans assuming an average water depth of 1000m), the water will rise 2.944E-012 m as a result of submerging the above object.
Airship
This is a very simple calculation. All you have to do is enter its gas containment capacity and Buoyancy will give you its lift. If your Airship, including its own structure, propulsion system and accommodation, weighs 118 tonnes and your lift capacity is 226 tonnes, you will have 108 tonnes available for cargo and additional equipment. Try this one for the Hindenburg airship:
| Input Data: | |
| altitude (a) | 200 {m} Hindenburg's normal flying altitude |
| internal pressure (pᴮ) | 102325 {N/m²} 1% higher than atm' pressure @ sea-level |
| common temperature (Ṯ) | 278.15 {K} about 5°C @ 200m |
| internal volume (V) | 200000 {m³} Hindenburg's gas carrying capacity |
| gas constant for internal gas (Rᵢ) | 4125.63 {N.m/kg/K} hydrogen |
| gas constant for atmospheric gas (Rₒ) | 286.771 {N.m/kg/K} air |
| Output Data: | |
| lift capacity [units of mass] (mᴸ) | 229,622.614118 {kg} buoyancy force required to lift the airship |
When designing an airship, it is important to take its normal operating altitude into account. The above lift capacity (mᴸ) is valid only for an altitude of 200 m, which was the Hindenburg's normal flying altitude. However, hovering just above sea-level, you would see 232 tonnes and at 1000 m its lift would be reduced to 202 tonnes.
If the Hindenburg had been filled with the less flammable gas; helium, its carrying capacity would have been reduced. Not only would helium itself have generated less lift (208 tonnes instead of 225 tonnes) but it is also heavier than hydrogen. Therefore, if the Hindenburg had been filled with helium, the gas alone (being 44.5 tonnes heavier) would have reduced the Hindenburg's cargo and equipment carrying capacity from 108 tonnes to 46.5 tonnes. So you can see why its designers preferred hydrogen to helium.
Helium Filled Balloon
Tethered: If you need to lift a cargo of 1kg to a height of 10,000m, and your cable weighs 0.02kg/m (total weight of 200kg), how big a balloon do you need?
| Input Data: | |
| mass carried (m) | 201 {kg} |
| inflated strain (e₁) | 1 {} inflated to twice its deflated surface area |
| burst strain (e₂) | 5 {} it will burst if surface area > 6 times its deflated size |
| balloon diameter (flat) (Ø₀) | 7.5 {m} |
| balloon wall thickness (t₀) | 0.001 {m} |
| balloon material density (ρᴮ) | 200 {kg/m³} |
| flexural modulus (E) | 60000 {N/m²} polymer version of Young's modulus |
| inflation air pressure (p₀) | 101325 {N/m²} atmospheric pressure at sea-level |
| inflated air density (ρᴬ) | 1.297 {kg/m³} surrounding air density at sea-level |
| fill gas density (ρᴳ) | 0.177 {kg/m³} helium |
| base-line height (h̲) | 7862.11353436002 {m} |
| Output Data: | |
| balloon diameter at e₁ (Ø₁) | 7.5 {m} spherical diameter when the surface area is doubled |
| balloon density at e₁ (ρ₁) | 1.16697 {kg/m³} including gas, balloon and cargo |
| balloon diameter at e₂ (Ø₂) | 12.990381 {m} spherical diameter when inflated to burst |
| balloon density at e₂ (ρ₂) | 0.049465 {kg/m³} including gas, balloon and cargo |
| burst altitude (aᴮ) | 12,961.089338 {m} altitude when balloon expands to burst |
| air pressure at aᴮ (pᴮ) | 19,487.688536 {N/m²} |
| air density at aᴮ (ρᴮ) | 0.24945 {kg/m³} |
| hover altitude (aᴴ) | 68,799.989209 {m} hover altitude if balloon hasn't burst |
| air pressure at aᴴ (pᴴ) | 16.042833 {N/m²} |
| air density at aᴴ (ρ) | 0.000205 {kg/m³} |
| quantity of fill gas [units of mass] (ρᴴ) | 39.104276 {kg} pressurised at sea-level |
The buoyancy force required to lift the balloon is the 'mass carried' + 'the weight of the balloon'
Despite the fact that, left to its own devices, this balloon would burst before it hovers, it is tethered to 10,000 m so it cannot burst.
Free-Float: If you want to get a helium filled balloon to hover without bursting and without tethering but to carry the same cargo (excluding the tether of course), you need to inflate the balloon just enough to initiate lift at sea-level. As soon as it gets off the ground the balloon's density will continue to decrease as it rises until it reaches hover altitude. Done properly (correct material, correct inflation, etc.), the balloon should reach its natural hover altitude before bursting. Try this example:
| Input Data: | |
| mass carried (m) | 1 {kg} |
| inflated strain (e₁) | 2.3 {} |
| burst strain (e₂) | 4.5 {} |
| balloon diameter (flat) (Ø₀) | 1 {m} |
| balloon wall thickness (t₀) | 0.00004 {m} |
| balloon material density (ρᴮ) | 200 {kg/m³} |
| flexural modulus (E) | 10000000 {N/m²} |
| inflation air pressure (p₀) | 101325 {N/m²} |
| inflated air density (ρᴬ) | 1.297 {kg/m³} |
| fill gas density (ρᴳ) | 0.177 {kg/m³} |
| base-line height (h̲) | 7862.11353436002 {m} |
| Output Data: | |
| balloon diameter at e₁ (Ø₁) | 1.284523 {m} |
| balloon density at e₁ (ρ₁) | 1.206507 {kg/m³} |
| balloon diameter at e₂ (Ø₂) | 1.658312 {m} |
| balloon density at e₂ (ρ₂) | 0.141938 {kg/m³} |
| burst altitude (aᴮ) | 6,696.525429 {m} |
| air pressure at aᴮ (pᴮ) | 43,232.259296 {N/m²} |
| air density at aᴮ (ρᴮ) | 0.55339 {kg/m³} |
| hover altitude (aᴴ) | 5,869.934522 {m} |
| air pressure at aᴴ (pᴴ) | 48,025.058475 {N/m²} |
| air density at aᴴ (ρ) | 0.61474 {kg/m³} |
| quantity of fill gas [units of mass] (ρᴴ) | 0.213255 {kg} |
The buoyancy force required to lift the balloon is the 'mass carried' + 'the weight of the balloon'
You will notice that to achieve this goal, you need a material with abnormally high strain capacity (e₂ = 4.5) for such a high flexural modulus (E = 10000000).
A conventional party balloon (with no cargo) can be made to hover without bursting if the following conditions apply:
| Input Data: | |
| mass carried (m) | 0 {kg} |
| inflated strain (e₁) | 2.25 {} |
| burst strain (e₂) | 16 {} |
| balloon diameter (flat) (Ø₀) | 0.04 {m} |
| balloon wall thickness (t₀) | 0.00015 {m} |
| balloon material density (ρᴮ) | 200 {kg/m³} |
| flexural modulus (E) | 60000 {N/m²} |
| inflation air pressure (p₀) | 101325 {N/m²} |
| inflated air density (ρᴬ) | 1.297 {kg/m³} |
| fill gas density (ρᴳ) | 0.177 {kg/m³} |
| base-line height (h̲) | 7862.11353436002 {m} |
| Output Data: | |
| balloon diameter at e₁ (Ø₁) | 0.05099 {m} |
| balloon density at e₁ (ρ₁) | 1.264036 {kg/m³} |
| balloon diameter at e₂ (Ø₂) | 0.116619 {m} |
| balloon density at e₂ (ρ₂) | 0.10566 {kg/m³} |
| burst altitude (aᴮ) | 19,747.743595 {m} |
| air pressure at aᴮ (pᴮ) | 8,220.022997 {N/m²} |
| air density at aᴮ (ρᴮ) | 0.10522 {kg/m³} |
| hover altitude (aᴴ) | 18,320.85632 {m} |
| air pressure at aᴴ (pᴴ) | 9,855.81884 {N/m²} |
| air density at aᴴ (ρ) | 0.126158 {kg/m³} |
| quantity of fill gas [units of mass] (ρᴴ) | 1.2345875E-005 {kg} |
The buoyancy force required to lift the balloon is the 'mass carried' + 'the weight of the balloon'
Hot Air Balloon
The hot air balloon does not use special gases to elevate. It uses air that has been made less dense through heating.
| Input Data: | |
| altitude (a) | 1000 {m} |
| inside temperature (Ṯᴮ) | 370.15 {K} |
| outside temperature (Ṯᴬ) | 283.15 {K} |
| balloon major diameter (Øᴮ) | 20 {m} |
| balloon height (hᴮ) | 20 {m} |
| fabric weight (wtᶠ) | 0.07 {kg/m²} |
| basket weight (wtᵇ) | 250 {kg} |
| ambient air pressure (p₀) | 102325 {N/m²} |
| gas constant for air (Rᴬ) | 286.771 {N.m/kg/K} |
| base-line height (h̲) | 7862.11353436002 {m} |
| Output Data: | |
| lift [units of mass] (mᴸ) | 801.357241 {kg} buoyancy force required to lift the balloon and its cargo |
| carrying capacity [units of mass] (C) | 447.599159 {kg} ≈3 people with baggage |
If you carry only 250 kg of cargo in the above balloon it will continue to rise until the effective densities (balloon and surrounding air) are equal, which would settle at 3220 m. Or you could reduce the internal air temperature to 71°C (344K). This is not a preferred option; however, as a reduced internal temperature will generate a lower internal pressure which will in turn loosen the envelope making it less controllable.
The normal technique for coping with this problem (preventing excessive altitude) is to take on board sufficient ballast (heavy weights) to compensate for the missing passengers. In the past, amateur ballooners would take too much ballast and throw out what they didn't need as they climbed to the correct altitude. The problems associated with this procedure are self-evident.
Calculator Input Data
Units
The units provided for the various calculation examples (above) are for information only.
You may use any units you like, but you must be consistent.
There is no default factor for gravitational acceleration in the calculation routines, so you may use pressure units of lbf/ft² instead of N/m².
There is sufficient information in the buoyancy calculator's 'Technical>Help' menu for you to perform typical calculations for all this program's calculation options.
Output Data
The buoyancy calculator will let you know if an obvious error has occurred. If, however, you get 'NaN' or 'infinity' you should check for incorrect input data or unacceptable zeros.
Further Reading
You will find further reading on this subject in reference publications(3)

