Flexible Beam Calculator
(for large non-linear deflections)
Non-linearity in beams applies to those ...
1) of an inconsistent construction (variable mass, bending stiffness and or shape), and;
2) that exhibit significant flexibility and therefore shorten (horizontally) under load.
Beams+ includes only the flexible type (2) above), which applies to those that deflect greater than 5% of their length.
Whilst most supporting structures limit deflections to 1 in 250 (or thereabouts), there are many applications where greater deflections are permitted and even desired, such as the installation of offshore flexible pipelines. It is for applications such as these that CalQlata has developed the formulas included in this calculator.
Units
You may use any units you like, but you must be consistent.
Cantilever
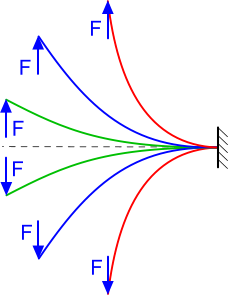
Fig 1. Flexible Cantilever
A cantilever is a beam with one fixed end and its entire length unsupported (Fig 1). A distributed load (e.g. self-weight), or a point load can be applied anywhere along its length. This type of beam is rarely used to support significant loads in functional structures not only due to its excessive deflections but because it always results in heavy sections.
As with all point-load beam calculations the beam's weight is ignored, which is perfectly acceptable if it is comparatively low. It is normal practice with conventional beams to perform two calculations, one for the distributed load and another for the point load, and simply add the deflections together, which is a pretty good approximation. A simpler approach may be used in 'Cantilever' by adding/subtracting the weight of the unsupported beam to the point load (F). See Flexible Beam Strength Calculator - Technical Help below.
Touchdown
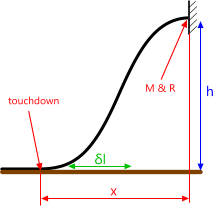
Fig 2. Touchdown Configuration
Touchdown refers to the point at which a very flexible beam or bar fixed at one end, touches down at the other end at a level well below the fixed end (Fig 2).
This type of configuration can be helpful as it allows for some relative movement in the supported length of the beam without imposing axial loads back into the structure. However, care must be taken to ensure that the bending moment (M) and bend radius (R) do not become damaging at the fixed end and the touchdown height should be kept to a minimum for beams sensitive to bending.
Stiffness

Fig 3. Sag Configuration
Bending stiffness is the resistance to lateral deflection and very important in the calculation of beams. In most cases, flexible beams tend to be manufactured from composites or polymers, the bending stiffness of which is unknown. The determination of bending stiffness in composites normally involves complex procedures that invariably include intrusion from external surfaces (rubbing or support) adversely affecting the result.
CalQlata's 'Stiffness' technique will provide you with an accurate value for bending stiffness with no interference from external surfaces.
You measure the straight length of your beam whilst it is supported on a flat surface. Put your beam in a rig (Fig 3) that fixes one end horizontally and guides the other end horizontally to a natural position of rest under its own weight, the freer the guide's movement the more accurate the result. If you know the weight of the beam, the amount the beam shortens will define its bending stiffness.
Fishing Rod
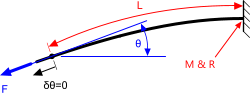
Fig 4. Fishing Rod Loading Condition
The name of this calculation option applies to the loading condition (Fig 4) not the resultant configuration and is only valid for beams with relatively (when compared to the above calculation options) small deflections, i.e. where the total deflection is less than 30% of the deformed length. Your beam may be any length you wish (even infinite) Fishing Rod will let you know how much of it is deformed and beyond which it will remain straight.
No matter how a beam of constant cross-section is loaded, the largest bending moment will always occur at the anchor, which will also be the location of the highest stresses and the smallest bend radius.
Compression Beam
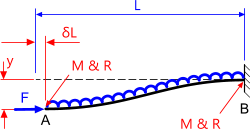
Fig 5. Axial Compression in a Bar
This option applies similar loading conditions to a column but with a co-incident lateral load (Fig 5). The calculation is for a beam with one end fixed, the other end guided, a uniform load (e.g. self-weight) applied over its entire length and a compressive axial load applied to its guided end.
This is a very sensitive calculation given that the loading condition is highly destructive. It would not be difficult to theoretically reverse-bend this beam, reversing one or both of the bending moments (Mᴬ or Mᴮ). The results from this calculation should be considered unreliable if; a) Mᴬ is negative; b) Mᴮ is positive; or c) the stress in the beam exceeds SMYS for the material.
You can determine the maximum stress in either end of this beam, using hand calculations or CalQlata’s Engineering Basics calculator {calculation option; 'BENDING (beam)'}. You could enter the Young’s modulus (E) for the beam material and the bend radius (Rᴬ or Rᴮ) or the second moment of area (I) for the beam section and the bending moments (Mᴬ or Mᴮ) along with the distance from the beam's neutral axis to its outermost fibre (y).
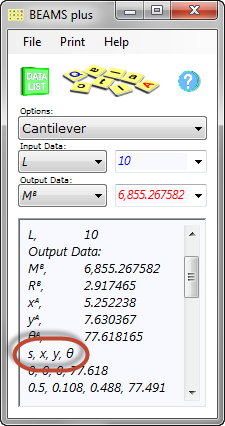
Fig 6. Cantilever Co-ordinates
No matter how a beam of constant cross-section is loaded, the largest bending moment will always occur at the anchor (end B), which will also be the location of the highest stresses and the smallest bend radius.
Flexible Beam Strength Calculator
Technical Help
Cantilever (calculation method)
The flexibility of 'Cantilever' has prompted us to provide co-ordinates of the configured beam. These are listed in the 'DataListing' page of the calculator below the Output Data, under the heading: 's, x, y, θ' (Fig 6). Select and copy all 20 lines of co-ordinates and paste them into your preferred spreadsheet (e.g. Microsoft Excel). You then set 'text-to-columns' using the comma as the delimiter and insert a scatter-chart using the middle two columns. The plot produced will pictorially represent your deflected beam (Fig 7).
As 'Cantilever's formula does not respond well to negative forces you must always apply a positive force (F) in Beams+. Therefore, you need to be careful with the application of forces and treatment of results when including the effects of self-weight and differentiating between lifting and sagging beams. For example; if you are lifting the end of a beam in the 'real world', you will need to add the weight of the unsupported length (w.L) to the lift force (F) generated in Beams+ (Fig 7). If on the other hand you are calculating a sagging beam, you must apply ⅜ of the weight of the unsupported beam at its tip in order to create the configuration of a beam sagging under self-weight only. You add to this figure any additional force you need to apply in the 'real-world' (Fig 7).
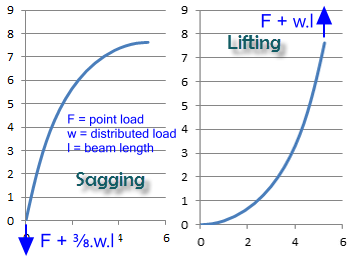
Fig 7. Cantilever Lift & Sag
Example 1: should you need to lift one end of a flexible beam off the floor, you should play with your length (L) and lift force (F) in 'Cantilever' until you achieve the desired configuration. You then add the weight of your lifted length of beam to the lift force ('F' entered in 'Cantilever') in order to find the force you need to apply to your beam in the 'real-world' to generate the same configuration. For example: if your beam weighs 200 N/m and you plan to lift 10 m of it off the floor, you must add 2000 N to the lift force (F) you input to 'Cantilever'.
Example 2a: if you want to determine the configuration of a beam sagging under its own weight, you use the same input data as Example 1 but the force (F) should be equal to ⅜ of its unsupported weight (Fig 8; 200 x 10 x 0.375 = 618.75 N).
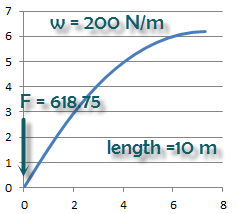
Fig 8. Cantilever Sagging
Example 2b: configuration of the same beam (as Example 1a) but using a force (F) of 1000 N would be that for a 'real-world' force of 381.25 N applied at its tip.
If either of the following occurs, your configuration will be unstable and you should try to tighten or stiffen it up. The configuration shown in Fig 11 is plot for a typical unstable calculation.
1) If you see a negative bending moment (Fig 9) in your output data, the length of your beam is too long for its stiffness and/or its end force is too low.
2) If a negative angle appears in the list of co-ordinates (Fig 10), the message "Your beam is too floppy/heavy, try reducing its length, or increasing its stiffness" will appear.
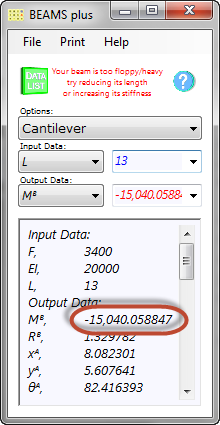
Fig 9. Cantilever '-ve' Moments
Touchdown (calculation method)
'Touchdown' is a stable calculation requiring no particular caution. As with all very flexible beams, however, if it has not been manufactured from homogeneous material, i.e. it's a composite construction, its bending stiffness (EI) may vary with deformation.
As such, you should first carry out a calculation with the value you have available and then re-measure the bending stiffness but now whilst deformed at the bend radius/bending moment (R, M) indicated by Touchdown. You should then recalculate using Touchdown but using the revised bending stiffness.
Stiffness (calculation method)
'Stiffness' is also a stable calculation requiring no particular caution, other than the value you get will be exact for the smallest bend radius generated at the centre of the beam (R). This stiffness value will apply equally to all deformations of the beam if it has been manufactured from homogeneous material and is of constant cross-section. If your beam is a composite, however, it is possible that its bending stiffness may vary at smaller bend radii.
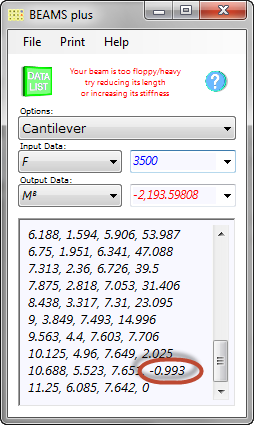
Fig 10. Cantilever '-ve' Angles
Fishing Rod (calculation method)
You enter the beam's bending stiffness (EI), tensile force (F) and angle (θ) of application and Fishing Rod will calculate the resultant bending moment and radius at the fixed end. It will also tell you where the beam straightens out (L) and the deflections (y) at the tip (x=0) and at a location designated by the User (x) anywhere in the deformed length.
Once you have the bending moment and radius at the anchor, you can use CalQlata's Engineering Basics calculator to calculate the maximum stresses generated in the beam as a result of the end load.
Compression Beam (calculation method)
You enter the beam's bending stiffness (EI), compression force (F), beam length (L) and weight per unit length (w), which can be self-weight or wind, or water or any other uniformally applied load along the entire length of the beam.
You can use CalQlata's Engineering Basics calculator to calculate the maximum stresses generated in both ends of the beam using either the bending moments and the second moment of area or the bend radii and Young's modulus of the beam material along with the distance from the beam's neutral axis out to its most extreme fibre.
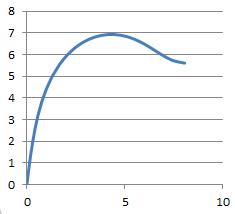
Fig 11. Cantilever Failed Calculation
Applicability
This calculator applies to beams with deflections greater than 5% of the beam's length.
CalQlata's Beams+ program is currently limited to beams with the following characteristics:
Constant cross-section throughout its length
Constant material throughout its length
Low bending stiffness when compared to the applied load
Longer unsupported length than a conventional beam
Obeys Hooke's law
Further Reading
You will find further reading on this subject in reference publications(1, 2, 3, 4 & 18)

