Aerofoil Lift Calculator (wings & spoilers)
Aerofoil is a general term for a wing or spoiler that provides lift or downforce, and aerodynamics is a term used to describe its performance when travelling through a gas, albeit; it more accurately refers to the behaviour of the gas within which the aerofoil is travelling.
In aerodynamics, 'air-speed' refers to the velocity of a shape relative to a gas (e.g. our atmosphere) through which it is moving; either a stationary shape within a moving gas, or a moving shape within a stationary gas, or a moving shape within a moving gas. All we are interested in is the relative movement; i.e. v = vs-vg
Where; vs is the velocity of the shape, and vg is the velocity of the gas in the direction of travel.
Improving aerodynamics simply means altering a shape to enable it to travel through a gas with greater speed whilst requiring less energy to do so. Manipulating aerodynamics means altering a shape to perform special actions as a result of such movement. A typical 'special action' is the deliberate induction of lateral force as a result of longitudinal movement.
In reality, a shape such as an aircraft wing (aerofoil) moves through a stationary# air column, which is not the case in wind tunnels.
# The relative velocity of a shape is modified by adding or subtracting 'wind-speed'; add for head-wind and subtract for tail-wind.
We know from Bernoulli that; the velocity of a gas is inversely proportional to its pressure. To induce a lateral force on a shape, the air velocity over one side of it must be greater than over the other side.
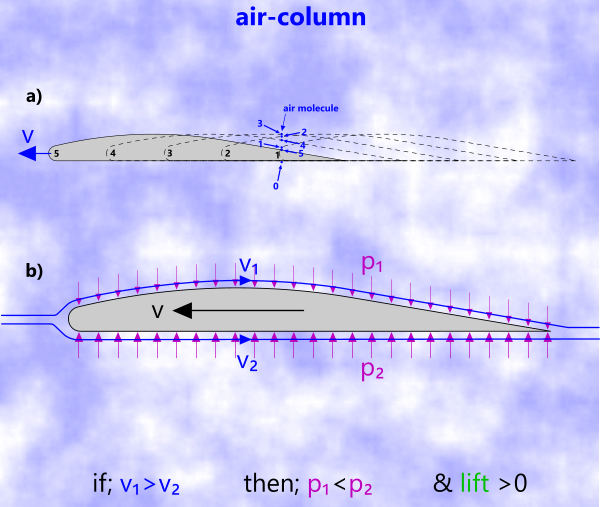
Fig 1 a), shows a typical aerofoil travelling through a column of air in a sequence of positions from 1 to 5. It isn't difficult to see that the molecules at the upper surface of this aerofoil (side-1) must travel further than those at its underside (side-2) in the same period; i.e. d₁/t > d₂/t so v₁ > v₂
Therefore, as shown in Fig 1, b), the pressure at the upper surface must be less than the pressure below it, resulting in natural lift, even if the underside angle is zero. However, for any given aerofoil mass (m), there is a minimum [relative] velocity below which it will not lift.
The principal factor in calculating the resultant lift (force) is called the dynamic pressure; q = ½.ρ.v²
However, 'q' is actually equivalent to pressure (not equal to it), because their units are not the same.
Therefore; q = p/CD
Where; CD is a ratio of lengths; so now the units match (see Accuracy below).
Note: v = √[2*q / ρ] ; where; 'q' is air pressure differential (δp) and 'ρ' is air density. When 2 is replaced with 'γ' and 'q' is replaced with 'pₐ' (atmospheric pressure), 'v' will be the speed of sound.
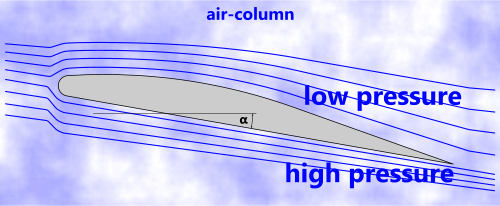
Fig 2. Angle of Attack (α)
A moving aerofoil is most efficient when presenting the lowest area to the direction of travel; i.e. its angle of attack (α) is zero. But this also generates the lowest lift (excluding negative values for α).
However, if 'α' is too high, the air trailing from its underside will be sucked into the low-pressure area (Fig 2) above the aerofoil, causing it to stall; which generally occurs at angles of attack (α) approaching 20°.
Today we use force and moment coefficients to help us describe aerodynamics using mathematics.
See Example Calculation 1 below.
The Aerofoil
The aerofoil (or wing) is a special case in aerodynamics. Its primary characteristic is that the distance from its leading edge back to its trailing edge is longer over its upper surface than on its underside. It is this that induces lift in an aircraft wing.
It is normal practice to ensure that dimension 'ac' (to the aerodynamic centre of the aerofoil) is approximately ¼.c
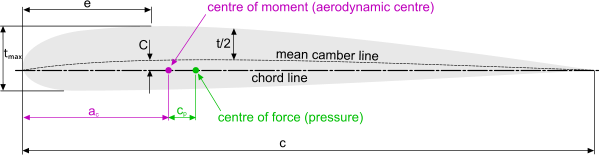
Fig 3. Principal aerofoil Dimensions
The principal dimensions that define an aerofoil's performance are provided in Fig 3
However, certain high-speed aircraft wings may have identical flow-paths (above and below) in order to minimise wing-section drag; these are generally referred to as low-drag wing-sections (refer to NACA). Lift is achieved only by altering the aerofoil's angle of attack (α).
The shape and orientation of an aircraft wing is a compromise between stability, manoeuvrability and drag.
Those of uniform width and oriented normal to a fuselage offer greatest stability (due to the high turning moments) but least manoeuvrability and greatest drag resistance.
In practice, transport aircraft, which benefit from stability tend to have long wings, and military aircraft, which favour manoeuvrability tend to have short (stubby) wings (Fig 4).
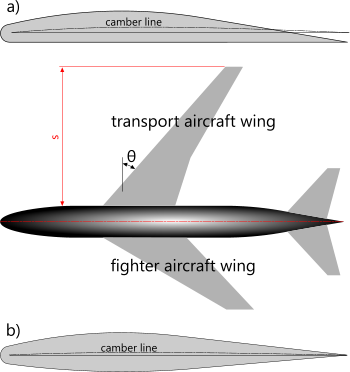
Fig 4. Aerofoil Applications
Both designs, however, will adopt a sweep-angle (θ) at the wing's leading edge to reduce drag; by Cos(θ).
In both cases, wings normally taper towards their tip, reducing the bending moments in the wing.
The aerofoil shapes displayed in Fig 4 give some idea as to the differences between the two requirements. Transport aircraft tend to use wings similar to example a) due to the greater lift capacity. Fighter aircraft will use variations based upon b) to minimise lift effects, giving the plane's thrust and its pilot freedom to determine aircraft behaviour.
The aspect ratio (Aᵣ) of an aerofoil is the ratio of its span-squared (Fig 4; s²) to its total area (A): Aᵣ = s²/A
Note: the general term 'wing-span' refers to the distance between wing-tips either side of a plane's fuselage.
Wind Tunnels
It is reasonable to assume that for all normal situations, relative velocities will be similar around a single airplane (for example) at any instant in time, which may not be the case in a wind tunnel. This is the reason test-flights tend to produce slightly different performance results to those achieved in wind tunnels.
The airflow generated in a wind tunnel is usually via an exposed axial fan. The problem with such an arrangement is that the airflow through an axial fan varies across its diameter; slowest at its centre and fastest at its periphery. If an accumulation chamber is not provided between the fan and the place of measurement, to allow the pressures to equalise, the results may not be totally representative. Therefore, one should be circumspect about accepting wind tunnel data without first understanding its design and operation.
Lift & Drag Coefficients
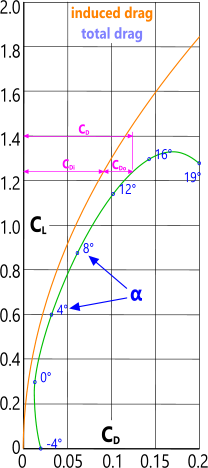
Fig 5. Lift vs Drag
The coefficients used to define lift and drag forces on an aerofoil are listed as follows:
Lift coefficient: CL refers to the coefficient that defines an upward force (L) operating normal to direction of travel;
Drag coefficient: CD refers to the coefficient that defines the force (D) operating in the opposite direction of travel;
Side coefficient: CS refers to the coefficient that defines an horizontal force operating normal to direction of travel (not shown);
Moment coefficient: CM refers to the coefficient that defines a turning moment that maintains aerofoil orientation.
All of these coefficients describe the shape in the direction of the force concerned, and they all apply similarly to the associated force formulas as described by Bernoulli:
L = CL.K D = CD.K M = CM.K.c
Where K = q.A
As is shown in Fig 5, the drag coefficient (CD) is the sum of two smaller coefficients; the induced drag coefficient CDi and the drag coefficient at zero lift CDo.
Forces and Moments
The two primary forces (lift and drag) are only valid if a moment exists. Without the moment (M), the aerofoil would simply lift, then rotate in the air and finally fall back to earth.
The lift force (L) on an aerofoil with different upper and lower surfaces at zero angle of attack is defined simply by the difference between the upper and lower air velocities (v₁ & v₂ Fig 1):
L = δp.A
Where; δp = p₂ - p₁ = p₂ . [v₂/v₁]²
p₂ is the atmospheric pressure on the underside of the aerofoil (Fig 1; b))
'α' values greater than zero will increase the lift force (L), causing the aerofoil to rise through the air. But as can be seen in Fig 5, an increase in lift will also increase drag, reducing forward velocity.
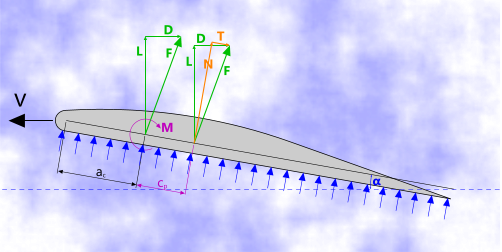
Fig 6. Aerofoil Forces and Moments
These calculations (α>0), are resolved by applying the above coefficients.
The forces shown in Fig 6) are also used to identify the stresses in a wing and therefore act as a design aid.
Aerofoils on Cars
Aerofoils are installed on fast cars to increase downforce (the opposite of lift) - which can be achieved by installing the aerofoil upside down. At first glance, few of the aerofoils (or spoilers) installed on vehicles appear to have been designed. Almost all of them appear to rely on an effective angle of attack less than zero, which will also increase drag and therefore reduce forward velocity; not particularly efficient!
However, with a properly designed spoiler, downforce could be achieved simply by designing a suitable aerofoil cross-section and installing it horizontally; minimising the effect of drag. Exactly the same calculations apply but instead of inducing lift, an equivalent level of downforce will be generated.
Aerodynamics Calculator – Technical Help
Units
You may use any units you like, but you must be consistent.
High-Lift Calculation Option
This calculation is for the design of a high-lift aerofoil, i.e. one that offers the greatest differential pressure (δp) across its section; a flat underside.
The principal aim of this calculation is to determine the angle of attack for zero lift (αₒ), which of course would be negative as it must compensate for the natural lift the aerofoil induces when horizontal.
αₒ is used for aerofoil performance calculation and angles of attack (α) greater than zero (refer to Performance Calculation Options below).
Low-Drag Calculation Option
This calculation is for the design of a low-drag aerofoil, i.e. one that offers the least differential pressure (δp) across its section; a curved underside.
The principal aim of this calculation is to determine the angle of attack for zero lift (αₒ), which of course would be negative as it must compensate for the natural lift the aerofoil induces when horizontal.
αₒ is used for aerofoil performance calculation and angles of attack (α) greater than zero (refer to Performance Calculation Options below).
Aerofoil Performance Calculation Option
This calculation determines the forces in any aerofoil providing uplift, such as an aircraft wing, and is based upon the graph shown in Fig 5.
However, its validity requires the input of an angle of attack for zero lift (αₒ), which can be entered manually by the user if known.
Whilst the input data for this calculation can be automatically transferred from either of the above design calculation options if preferred, it should be noted that if any of the input data - other than the angle of attack (α) - is subsequently altered, the results will be compromised because 'αₒ' will no longer be correct.
See Accuracy below.
Spoiler Performance Calculation Option
This calculation determines the forces in any aerofoil providing down-force, such as a vehicle spoiler, and is based upon the graph shown in Fig 5.
However, its validity requires the input of an angle of attack for zero lift (αₒ), which can be entered manually by the user if known.
Whilst the input data for this calculation can be automatically transferred from either of the above design calculation options if preferred, it should be noted that if any of the input data - other than the angle of attack (α) - is subsequently altered, the results will be compromised because 'αₒ' will no longer be correct.
See Accuracy below.
Example 1
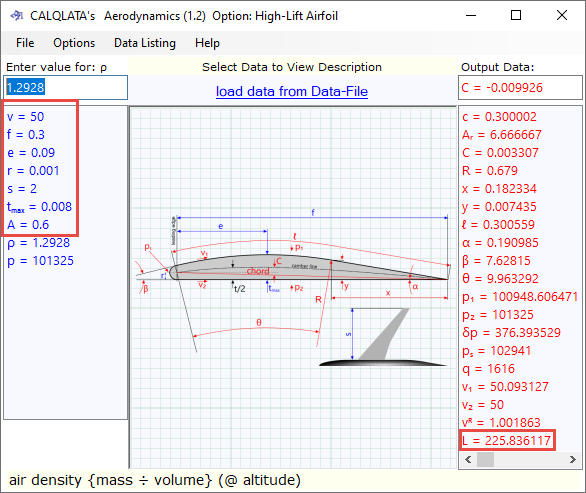
This example applies to both the high-lift and low-drag calculation options.
Fig 7; the input values are entered (LHS) according to the illustration provided and the output data is provided on the RHS.
You will notice that the chord line is not horizontal in the high-lift calculation option, and it is calculated (c), not entered. This is done deliberately to demonstrate how much lift can be achieved with a simple, flat aerofoil if correctly designed.
This is by far the most appropriate design for a vehicle spoiler as it provides maximum down-force with minimum drag.
The calculation shown here (Fig 7) reveals a potential 225kg (almost a ¼-tonne) down-force from a spoiler just 8mm thick and 300mm wide when travelling at 50m/s (112 mph), and less than 2N drag force (<0.2kg)!
Add another at the front, and you have almost half a tonne of down-force and next to zero drag and very little added weight.
It therefore begs the question:
Why do we see such enormous spoilers on sports and racing cars tilted to increase down-force, but also increasing drag; i.e. reducing speed and raising fuel consumption?
Example 2
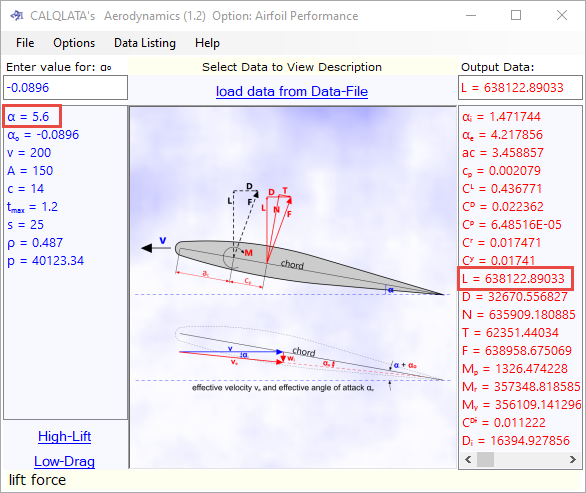
This example applies to both aerofoil and spoiler performance calculation options.
Fig 8; the input values are entered (LHS) according to the illustration provided and the output data is provided on the RHS.
You will notice that this calculation option offers two possible import options; 'High-Lift' and 'Low-Drag' (bottom-LH corner of the window). Click either and the data from the associated aerofoil design option will be automatically inserted into the input data here.
Careful though, once inserted, it is wise to alter only the angle of attack (α). Alter anything else and the calculation results will be unreliable, because the zero-lift angle (αₒ) will no longer be reliable.
However, this is a stand-alone calculation option if you wish it to be:
If you have representative input data and wish to enter it manually, without reference to the aerofoil design calculation options you may do so, the results will be perfectly valid.
Whilst it is based upon the same mathematics, this calculator is not expected to replace a commercially available aircraft design software, it is provided for general calculations that may be used by interested parties, verification and/or model makers.
This calculation reveals that two aerofoils (wings) of the properties shown will lift 130 tonnes with an attack angle of just 5.6°
As indicated in the respective illustrations;
when calculating lift aerofoils, the angle of attack should be entered positive when rotated clockwise;
when calculating down-force aerofoils, the angle of attack should be entered positive when rotated anti-clockwise.
Only these two calculation options provide plot data (Data Listing>Plot Co-ordinates) for various angles of attack.
Input Data
v; aerofoil velocity
f; aerofoil length (high-lift option)
e; distance from leading edge to maximum thickness
c; chord length (low-drag option)
r; radius of leading edge
s; aerofoil span (not length)
tₘₐₓ; maximum aerofoil thickness (high-lift option)
t₁ₘₐₓ; maximum aerofoil thickness above chord-line (low-drag option)
t₂ₘₐₓ; maximum aerofoil thickness below chord-line (low-drag option)
A; section area through aerofoil chord
ρ; air density (at altitude)
p; air pressure (at altitude)
αₒ; angle of attack for zero lift (high-lift and low-drag calculation options)
α; operational angle of attack (performance calculation options)
Output Data
Aᵣ; aerofoil aspect ratio
ac; distance from aerofoil leading edge to moment (aerodynamic centre)
c; chord length (high-lift option)
C; maximum camber
ℓ; length of upper surface (high-lift option)
ℓ₁; length of upper aerofoil surface (low-drag option)
ℓ₂; length of lower aerofoil surface (low-drag option)
R; radius of upper surface curved profile (high-lift option)
R₁; radius of upper surface curved profile (low-drag option)
R₂; radius of lower surface curved profile (low-drag option)
tₘₐₓ; maximum aerofoil thickness (low-drag option)
x; length of upper surface straight profile (high-lift option)
x₁; length of upper surface straight profile (low-drag option)
x₂; length of lower surface straight profile (low-drag option)
y; maximum height of upper surface straight profile (high-lift option)
y₁; maximum height of upper surface straight profile (low-drag option)
y₂; maximum height of lower surface straight profile (low-drag option)
α; angle of attack
αₒ; zero-lift angle of attack
αᵢ; induced angle of attack
αₑ; effective angle of attack
β; angle of upper surface at leading edge (high-lift option)
β₁; angle of upper surface at leading edge (low-drag option)
β₂; angle of lower surface at leading edge (low-drag option)
θ; sweep angle of upper curved surface (R)
θ₁; sweep angle of upper curved surface (R₁)
θ₂; sweep angle of lower curved surface (R₂)
p₁; average pressure on upper surface of aerofoil
p₂; average pressure on lower surface of aerofoil
δp; pressure differential (p₂-p₁)
pₛ; static pressure (at leading edge)
q; dynamic pressure
v₁; air velocity over upper surface
v₂; air velocity over lower surface
vᴿ; velocity ratio
vₑ; effective velocity
cₚ; pressure coefficient
Cᴸ; lift coefficient
Cᴰ; drag coefficient
Cᴰᶤ; induced drag coefficient
Cᵖ; pitch moment coefficient
Cʳ; roll moment coefficient
Cʸ; yaw moment coefficient
L; lift force
D; drag force
Dᵢ; induced drag force
N; normal (to aerofoil chord) force
T; tangential (to aerofoil chord) force
F; resolved force
wᵢ; downwash force
Mₚ; pitch moment
Mᵣ; roll moment
Mᵧ; yaw moment
Applicability
This calculation is applicable for any aerofoil of the shape shown in Fig 3 above.
Accuracy
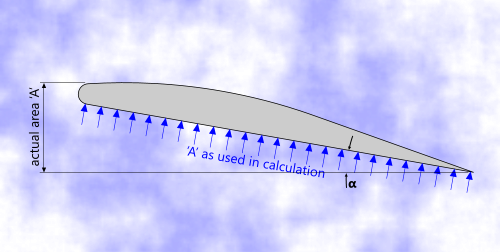
Fig 9. Actual Projected Area vs Area Used in Calculations
We are all aware of Morison's formula for force induced due to fluid pressure;
F = CD.½.ρ.A.v²
where 'A' is the area hit by the fluid travelling at velocity 'v'
If we then divide both sides by the area, we get:
pressure; p = CD.½.ρ.v²
where dynamic pressure; q = ½.ρ.v²
This gives us; p = CD.q
and if we multiply this by area we get; F = CD.q.A
which is the calculation method for aerofoil forces and pressures.
Therefore, forces and pressures are entirely dependent upon the validity of a coefficient. And if we look at the range of values for CD in Fig 5, they look very low; we would normally expect values between 0.5 and 1.0
The reason for this anomaly is due to the area used in the standard calculation method. Under normal circumstances, we could calculate such a resistance [force] based upon actual area 'A' in Fig 9, and not the sectional area of the aerofoill.
As such, the normally expected value for CD must be multiplied by Sin(α), hence the unexpectedly low value-range in Fig 5.
Therefore, whilst the relationship between lift and drag coefficients are based upon experiment and practice over many years, they can only ever be approximate.
CalQlata would suggest an accuracy of ±20% when using this calculation procedure for an entire wing of non-uniform shape and section. But this tolerance can be reduced to ±10% if the calculation is carried out repeatedly on, say, 1m strips of an aerofoil and combined in a spreadsheet.
Further Reading
You will find further reading on this subject in reference publications(1, 3, 17 & 34)

