Friction Coefficient Calculator
& universal self-holding tapers
The resistance to relative movement between any two contacting surfaces under load normally occurs as a result of the mechanical interlocking of sharp undulations in the two mating surfaces and is called friction.
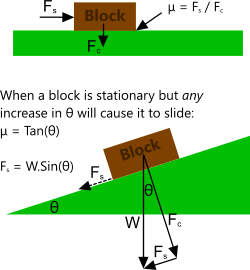
Fig 1. Friction Coefficient
Frictional resistance is mathematically defined for a block moving along a flat surface, as the ratio of sliding force (Fs) to contact force (Fc)
i.e. μ = Fs ÷ Fc (Fig 1)
(where 'μ' is called the coefficient of friction)
If the Block is placed on a sloping surface, 'μ' is equal to the tangent of the angle of the slope (θ) at the point of transition between relative slide and hold conditions for these two materials (Fig 1)
E.g.: For a coefficient of friction of 1.0 this angle is 45°
'μ' can be modified by changing the contacting materials, their relative surface roughness or introducing a foreign substance such as a lubricant or chemical agent between the two surfaces.
Two clean, perfectly smooth and infinitely hard surfaces will offer no resistance to relative movement (μ = 0).
Two rough connecting surfaces joined together with a high-shear fluid (such as treacle) can result in a frictional resistance ('μ') greater than 1, that is: the force necessary to induce relative movement can be greater than the contact force between them.
Problems of Friction
Friction will always result in wear between two moving surfaces in contact and under load, such as in bearings, and this wear will ultimately result in operational failure if dimensional stability is important between the two mating surfaces.
Friction will also result in increased temperature and noise, both of which usually result in power and energy losses and therefore operational inefficiency.
Benefits of Friction
Frictional resistance is useful in driving mechanisms that are designed to slip if loads become excessive, such as a clutch, or where adjustable grip is required such as braking systems.
Self-Holding Tapers
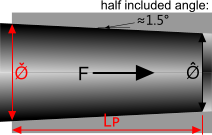
Fig 2. Self-Holding Tapers
A special case for the beneficial use of friction is 'self-holding' Tapers (Fig 2) for easy machine/equipment component assembly and disassembly such as drill chucks and lathe tail-stock accessories.
A self-holding 'Taper' is an accurately machined tapering shaft and mating sleeve (both of which are dry and clean) that lock together using the coefficient of friction between the two surfaces (shaft and sleeve) and an assembly force (F). If the Taper is machined correctly, the same force (F) will be needed to separate the shaft and sleeve.
If the angle of the Taper is 'exactly right', the shaft or sleeve will be capable of driving the other with no additional assistance for light duty applications and yet part easily with no resultant damage to either of the mating surfaces.
It is important to remember that a plain self-holding taper is only capable of transmitting a force achievable from 'frictional' grip and is thereby limited in its driving capacity. For heavy duty applications the taper is usually provided with a key, the frictional grip providing the holding capacity only.
Morse Taper
In the mid-19th century, Stephen Morse devised the self-holding Taper based upon an included (diametral) slope of 5/8th of an inch for each foot of contact length (≈3°), which has become recognised as the Morse Taper. Morse's Taper is based upon a coefficient of friction between mating surfaces of 0.8 (i.e. clean, dry, ground, carbon steel).
There are 8 sizing grades for Morse's taper (0-7) using standard diameters and mating lengths dependent upon loading capacity. These are listed as follows:
| Grade: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Minor Dia. Ø̂ | 0.252 | 0.369 | 0.572 | 0.778 | 1.02 | 1.475 | 2.116 | 2.75 |
| Major Dia. Ø̌ | 0.3561 | 0.475 | 0.7 | 0.938 | 1.231 | 1.748 | 2.494 | 3.27 |
| Plug Length (Lᴘ) | 2 | 2.125 | 2.5625 | 3.1875 | 4.0625 | 5.1875 | 7.25 | 10 |
Dimensions in the above Table are inches
The diameters specified in the above Table (Ø̂ and Ø̌) are at either end of the Plug Length (Fig 2)
The Plug Length (Lᴘ) is the contact length between the shaft and the sleeve
But Stephen Morse was not the only designer of self-holding tapers and they needn't apply only to carbon-steel; they are indeed universal and can be applied to any combination of materials, as is demonstrated in Friction.
Jarno Taper
Oscar James Beale optimised the sizing of Morse's Taper, which is so clever that whilst it is virtually the same angle as the Morse Taper (2.8642° vs 2.981°) it has been individually recognised under his Pen-Name as the 'Jarno Taper'.
Taper Design
The Morse Taper is ≈3° for a reason. An optimum correlation between taper angle, length and coefficient of friction provides the self-holding facility for which the Taper is intended. It's all based upon the same shaft extraction load as that applied for insertion and the coefficient of friction for carbon steel (0.8).
Rules for the Coefficient of Friction
1) For conditions of negligible surface deformation, the friction coefficient is proportional to contact surface pressure
2) Friction is independent of surface contact area
3) For conditions of negligible surface heating and/or degradation, friction is independent of relative velocity (between the two surfaces)
Friction Coefficient Calculator - Technical Help
Units
You may use any units you like, but you must be consistent.
Angle of Repose
Stiction
As the coefficient(s) of friction between any two materials sliding relative to each other and under load is their angle of repose, you can accurately find the value of 'μ' for any two materials as described below (Fig 3).

Fig 3. Measuring Stiction
1.1) Make an adjustable sloping base from one of the materials with the appropriate surface condition and finish
1.2) Make a block from the other material again with the correct surface condition and finish
1.3) Adjust the sloping base to an horizontal gradient
1.4) Place the block on the sloping base
1.5) Raise one end of the sloping base slowly (and carefully) until the block starts to slide
1.6) Repeat 1.5) above as many times as necessary to ensure an accurate value for 'θ'
1.7) Measure dimensions 'x' and 'y' (Fig 3)
1.8) Calculate: μ = y÷x (using calculation option 'Frictional Slide')
The above 'μ' is the coefficient of 'stiction', sometimes referred to as the coefficient of 'friction initiation'.
Friction
To calculate the coefficient of friction for the same materials a little more care is required, but an accurate result can be found as follows (Fig 4):
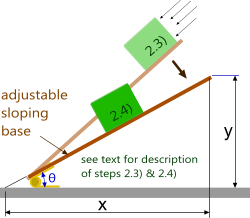
Fig 4. Measuring Friction
2.1) Take the above sloping base and block
2.2) Lift one end of the sloping base to an angle greater than that for the angle of stiction (above)
2.3) Place the block on the sloping base at the highest point (Fig 4) and allow it to slide
2.4) Reduce the angle of the sloping base whilst the block is sliding until it stops 'mid-slide' on its own
2.5) Repeat 2.3) and 2.4) above until you can start the slide and stop it again 'mid-slide' simply by adjusting the angle of the base
2.6) When you have managed to find the exact angle at which the block stops mid-slide you measure dimensions 'x' and 'y' (Fig 4)
2.7) Calculate: μ = y÷x (using calculation option 'Frictional Slide')
The above 'μ' is the coefficient of 'friction'.
The coefficient of stiction is normally about 10% greater than the coefficient of friction, however this is very much dependent upon the two materials and their relative surface condition.
The greater your accuracy in measuring the above angles (θ), the more accurate your coefficients will be.
Frictional Slide
Once you have identified a value for μ (see Angle of Repose above) you can enter this value in calculation option 'Frictional Slide' along with an inclination and slide distance and Friction will tell you how quickly the block will reach the bottom along with the acceleration and kinetic energy.
Tapers
Whilst Morse's Taper was originally designed for carbon steel surfaces (μ = 0.8), the friction coefficient calculator can predict the angle of a Taper manufactured for any coefficient of friction, i.e. any material combination and surface condition but with the same self-holding capacity as Morse's Taper of the same Grade.
The friction coefficient calculator gives you the option of selecting a recommended (by CalQlata) coefficient of friction via a series of material combination options or you may enter your own independent value. Whilst Friction will accept any value for 'μ' in accordance with our 'GiGo' principal, values less than or equal to 0 will result in failed calculations or negative angles, and values for 'μ' greater than 3, whilst theoretically correct, will usually give unrealistic results.
The calculation in this option applies the modified Taper angle (θ) to the same minor diameter (Ø̂; Fig 2) and contact surface area as the original Morse Taper for your selected Grade ('G' see Morse Taper above). In other words, should you manufacture a Taper to the dimensions provided by the friction coefficient calculator for the materials you have selected ('μ') the assembly will have the same 'self-holding' capacity as Morse's carbon steel Taper for the same Grade.
Note: The included angle used as the basis for the Morse Taper in the friction coefficient calculator is 2.9745503204919° as this is the optimum angle for the friction coefficient of 0.8 in his designs.
Further Reading
You will find further reading on this subject in reference publications(2 & 3)

