Trigonometry Calculator (triangles)

Fig 1. External & Internal Angles
A Few Trigonometry Facts
The sum of all three angles in any triangle is always exactly 180°.
The length of the longest side of any triangle is always shorter than the sum of the two other sides but greater than their difference.
The smallest angle in any triangle is always opposite its shortest side.

Fig 2. Circumscribed Circle
The largest angle in any triangle is always opposite its longest side.
An exterior angle is always equal to the sum of the two opposite interior angles (Fig 1).
All three vertices of a triangle always lie on the circumference of a single, common circle, called the 'circumscribed' circle (Fig 2).
All three Perpendicular Bisectors of any triangle always meet at the same point, which is the centre of its circumscribed circle (Fig 2).
A circle that fits exactly inside any triangle and whose circumference touches all three sides (at a tangent) is called its 'inscribed' circle (Fig 3).
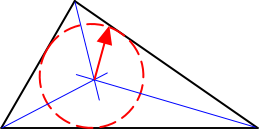
Fig 3. Inscribed Circle
All three 'Angular' Bisectors (a line that divides an angle in two) of any triangle always meet at the same point, which is the centre of its inscribed circle (Fig 3).
All three 'Medians' of any triangle always meet at the same point, which is the centre of gravity of the triangle (Fig 4).
If one of the angles is exactly 90°, the side opposite to this angle is always equal to, and lies upon, the diameter of the circumscribed circle (Fig 7).
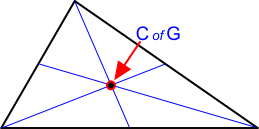
Fig 4. Centre of Gravity
Trigonometry Definitions
The dedicated terms (or acronyms) used here for specialised triangles and angles and their component parts (e.g. Perpendicular, Bisectors, Centre of Gravity, Equilateral, Isosceles, Obtuse, Acute, Right-Angle, etc.) are all described in the Definitions page of this web site.
Right-Angle Triangles
The sides and/or angles of any right-angle triangle (where one of its angles is exactly 90°, Fig 5) can be calculated by using the following trigonometrical terms and their reciprocals:
The sine of an angle: sin(A) = opposite ÷ hypotenuse {the inverse is its 'arc' value; asin(A)}
The cosine of an angle: cos(A) = adjacent ÷ hypotenuse {the inverse is its 'arc' value; acos(A)}
The tangent of an angle: tan(A) = opposite ÷ adjacent {the inverse is its 'arc' value; atan(A)}

Fig 5. Right-Angle Triangle
Their reciprocals are defined thus:
Cosecant of an angle: csc = 1/sin
Secant of an angle: sec = 1/cos
Cotangent of an angle: cot = 1/tan
Values for each of the above trigonometrical terms can be determined without calculators or Tables as follows (where the angle 'A' must be specified in radians):
sin(A) = A - A³÷3! + A⁵÷5! - A⁷÷7! + A⁹÷9! - A¹¹÷11! + A¹³÷13! - A¹⁵÷15! + … etc.
cos(A) = 1 - A²÷2! + A⁴÷4! - A⁶÷6! + A⁸÷8! - A¹⁰÷10! + A¹²÷12! - A¹⁴÷14! + … etc.
tan(A) = sin(A) ÷ cos(A)
Note: πᶜ = 180°
For a complete and detailed explanation of the properties of 'Sine', 'Cosine' and 'Tangent' of an angle and how they are derived, see Trig Functions
Oblique Triangles
No angle in the triangle is 90° (Fig 6). These can be calculated using the relationships shown below:
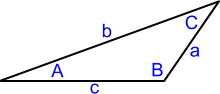
Fig 6. Oblique Triangle
The law of sines:
sin(A)÷a = Sin(B)÷b = Sin(C)÷c
The law of cosines:
a² = b² + c² - 2.b.c.cos(A)
b² = a² + c² - 2.a.c.cos(B)
c² = a² + b² - 2.a.b.cos(C)
The law of tangents:
(a+b)÷(a-b) = tan(½[A+B])÷tan(½[A-B])
(a+c)÷(a-c) = tan(½[A+C])÷tan(½[A-C])
(a+b)÷(b-c) = tan(½[B+C])÷tan(½[B-C])
Trig Plus provides solutions for more complex trigonometrical relationships
Trigonometry Calculator - Technical Help
Triangles
1) Always observe the above facts ('A Few Facts')
2) The length of every side must be greater than 0 (see note below)
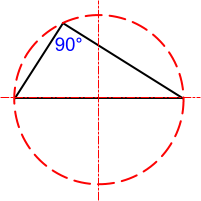
Fig 7. 90° & Circumscribed Circle
3) Every angle must be greater than 0° (see note below)
4) Every angle must be less than 180° (see note below)
5) You only need to know three parameters of any triangle (i.e. its angle and its sides) in order to establish everything else about it with one exception; see rule 6 below
6) You cannot define a triangle by knowing only its three angles
7) Pythagoras' theorem only works with right-angle triangles
Note: In accordance with CalQlata's GiGo principle (refer to 'Entering Data' in the 'General Help' page on this web site), you may of course enter any value you like in Trigonometry and any viable result (even a negative one) will be correct. The problem with such practices is that it can make orientation of the resultant triangle a little difficult.
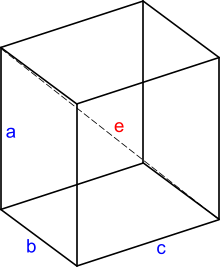
Fig 8. 3-D Pythagoras
3-D Boxes
Every right-angled box (Fig 8) has three 'Face' hypotenuses each with two equal right-angle triangles and a single compound (internal) hypotenuse ('e') with two equal compound right-angle triangles. If you know the length of all three sides you can establish the lengths of all hypotenuses and their angles.
As a point of interest, did you know that Pythagoras' theorem also works in 3-D? i.e. e² = a² + b² + c²
Sectors & Segments
'L' is an Arc of a circle (Fig 9).
'e' is a Chord of the above Arc (Fig 9).
The Segment of this construction is enclosed by 'L' and 'e'.
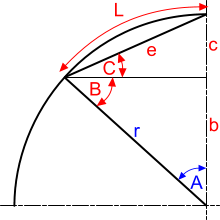
Fig 9. Parts of a Circle
The Sector of this construction is enclosed by 'L' and the two radii 'r' and 'b+c'. If you remove its Segment, the shape becomes an isosceles triangle.
A 'Subtended Angle' (Fig 9; 'A') is the angle opposite the Chord of a Sector.
Trig (Trigonometry) will accommodate any Subtended Angle ('A') between 0° and 180°. However, if you enter a Subtended Angle greater than 90°, length 'b' and opposite angle 'B' (Fig 9) will become negative and the shape of the Sector/Segment will be defined by length 'c' and opposite angle 'C' (Fig 9).
Further Reading
You will find further reading on this subject in reference publications(3 & 12)

