Engineering Basics Calculator (the fundamentals)
The engineering basics you will fing in this calculator are the fundamentals upon which almost all other engineering calculations are based.
All of the calculation options in Engineering Principles work similarly. You simply continue to enter all known values until a result appears for the Output Data you require (assuming no error message is displayed). Engineering Principles will simply calculate all the unknowns it can with the information you provide.
There are two calculation techniques in Engineering Principles; 'simple' and 'complex' and each option is labelled as such below. The rules for both are as follows:
Rule 1 (common to both types):
Engineering Principles assumes that all variables are zero.
You enter those you know and once the calculator has sufficient information, it will provide you with an answer.
If you enter too much information, Engineering Principles will ask you to "delete the unknown".
Rule 2 (simple):
There is only one equal sign in the formula.
You need to know all the variables except one.
Engineering Principles will calculate the only unknown as soon as it has all the other data.

Fig 1. Beam Bending
Rule 3 (complex):
The formula contains more than one equal sign.
You enter whatever information you have, and
Engineering Principles will calculate whatever unknowns it can with the data provided.
You need to follow Rule 2 for any two of the three factors available in the equation.
Units
You may use any units you like, but you must be consistent.
BENDING (beam) (complex)
This option is used to establish the performance characteristics of a beam of constant cross-section and material under direct bending Fig 1.
Whilst the beam continues to obey Hooke's law, it will behave in an entirely predictable manner. You can predict its unknown properties simply by knowing certain others. This relationship is governed by the well-known formula;
σ÷y = M÷I = E÷R
(where σ = stress, y = distance from neutral axis, M = bending moment, I = 2nd moment of area, E = Young's modulus and R = bend radius @ the neutral axis).

Fig 2. Bar Torsion
TORSION (bar) (complex)
This option is used to establish the performance characteristics of a bar under direct torsion Fig 2.
Whilst the bar continues to obey Hooke's law, it will behave in an entirely predictable manner. You can predict its unknown properties simply by knowing certain others. This relationship is governed by the well-known formula;
τ÷r = T÷J = Gθ÷L
(where τ = shear stress, r = radius from centre of rotation, T = torque, J = polar moment of inertia, G = shear modulus (or modulus of rigidity), θ = angle of twist and L = length of twist).
COMPRESSION (column) (complex)
This option is used to establish the performance characteristics of a column under direct tension or compression Fig 3.
Whilst the column continues to obey Hooke's law, it will behave in an entirely predictable manner. You can predict its unknown properties simply by knowing certain others. This relationship is governed by the well-known formula;
E = F÷A = σ÷e
(where E = Young's modulus, F = axial force,
A = cross-sectional area, σ = tensile stress,
e = axial strain).

Fig 3. Column Compression
FLUID IN-OUT (simple)
This option (devised by Bernoulli) defines the relationship between the Head, Pressure and Velocity of a fluid flowing through a pipe (assuming no losses). This relationship is described by the formula;
Z₁+p₁ ÷ ρ+v₁² ÷ 2g = Z₂+p₂ ÷ ρ+v₂² ÷ 2g
(where Z = Head, p = pressure, ρ = fluid density, v = fluid velocity, g = acceleration due to gravity)
For more detailed/accurate fluid flow calculations (through a pipe) see CalQlata's Pipe Flow calculator.
SPRING/FREQUENCY (simple)
This option defines the vibration characteristics of a mass mounted on a sprung support. Virtually every solid structure has an inherent stiffness and can therefore be described as a 'spring'. This relationship is defined by the formula: ƒn = √(k÷m) / 2π
(where ƒn = natural frequency {Hz}, k = stiffness {N/m} and m = mass {kg} units are provided here for guidance only (refer to Units).
You can use this formula, for example, to make sure that the mountings used to support a motor do not share its natural frequency.
Use CalQlata's Spring Coefficients calculator for values of 'k'.
MOTOR POWER (simple)
This option uses the well-known formula; P = 2πNT to calculate the relationship between power, torque and rotary speed
(where P = power, T = torque and N = revolutions per second) to define the relationship between power, rotary speed and torque.
ELASTIC CONSTANTS (complex)
This option defines the elastic behaviour of materials via three well-known equations;
E = σ÷e, G = E ÷ 2(1+ν) and K = E ÷ 3(1-2ν)
(where σ = stress, e = strain, E = Young's modulus, G = shear modulus, K = bulk modulus and
ν = Poisson's ratio).
Together, these formulas describe the two and three-dimensional behaviour of any given material and all are directly related to each other. Therefore, if you know enough of the variables in any one equation, you can calculate all the others, so long as the material obeys Hooke's law.
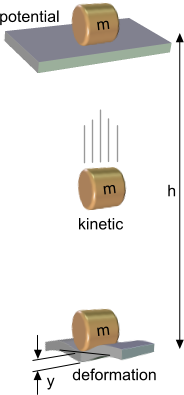
Fig 4. Energy Conversion
ENERGY (complex)
This option takes whatever you know in full or in part about any of the three forms of energy shown in Fig 4 (potential, kinetic and deformation) and fills in all the gaps it can assuming no losses from heat, noise, damage, etc.
Note: If you enter a value greater than zero for the spring constant 'k' in this calculation, Engineering Principles will assume the deformation (y) to be completely elastic, i.e. there will be no subsequent evidence of the impact and the force 'F' generating the deformation will be an average force. In any fully elastic deformation the force ranges from zero (0) when the spring is relaxed to twice the average force (2F) when the spring is fully compressed or extended. In a completely non-elastic (plastic) deformation, you should set 'k' to zero whereupon the force (F) is assumed to be constant throughout the deformation.
Note: Velocity in this calculation refers to 'final' velocity, immediately before impact (see CalQlata's Fluid Forces calculator for terminal velocity calculations).
IDEAL GAS LAW (simple)
This option describes the relationship between the pressure, temperature and volume of a gas (or any other compressible fluid). A rise in temperature will raise the pressure (and vice-versa) for any given fluid and constrained volume. The opposite occurs if you raise the volume.
The formula for the ideal gas law (P.V = n.Rᵢ.Ṯ) may be used to calculate the unknown property of a given gas under specified conditions or it can be used to find an unknown property when comparing two different but equivalent gas conditions (P₁.V₁ ÷ n₁.Rᵢ.Ṯ₁ = P₂.V₂ ÷ n₂.Rᵢ.Ṯ₂);
'n' in this formula is the number of moles of gas, which is usually an awkward property for most of us to deal with. As 'n' equals mass ÷ RAM of the gas atom or molecule and is much easier to handle, CalQlata has included the mass (m) and relative atomic mass (RAM) values as input data in the engineering basics calculator.
Therefore, the formula used in this calculation option is modified to P.V = m.Rᵢ.Ṯ ÷ RAM
CalQlata's Elements includes the relative atomic mass of all the atoms and can also calculate the RAM of any molecule you require.
If you set all the gas₂ properties to zero, Engineering Basics will assume that you are calculating the unknown property of a single gas and will inform you of the need for more data or to delete the unknown accordingly.
If any of the gas₂ properties are not equal to zero, Engineering Basics will assume that you are comparing the unknown property between two gases and will inform you of the need for more data or to delete the unknown accordingly.
The gas constant (Rᵢ) must not be zero. Imperial and metric values for the gas constant are provided in the engineering basics calculator.
You should ensure that you are using compatible units for all the input data.
Example units you may use in this calculation are provided as follows:
P = pressure (N/m²)
V = volume (m³)
m = mass of gas (g)
RAM = relative atomic mass of gas (g/mole)
Rᵢ = 8.3143 J/K/mole
Ṯ = temperature (K)
The units cancel out as follows:
N ÷ m² x m³ = g x J x K ÷ K ÷ mole ÷ K ÷ (g/mole) = N.m (Joules)
You may use other units as long as you are consistent.
CAPSTANS (simple)

Fig 5. Capstan restraint loading
This option uses the formula T1=T2eμθ to define the relationship between the tensions in each end of a rope wrapped around a capstan (or any circular pillar) Fig 5.
(where T1 is the holdback force (applied by you) and T2 is the force you're trying to restrain. μ is the coefficient of friction between the rope and the capstan and θ is the angle of contact the rope has with the capstan).
Engineering Principles does not ask you for an angle and it doesn't provide one in the answer. It deals with turns (or wraps) around the capstan. Exactly one full turn is equal to 360° (i.e.: 180° = 0.5 turns and 1080° = 3 turns).
Further Reading
You will find further reading on this subject in reference publications(1, 2 & 3)

