Second Moment of Area Calculator
(area moments, moment of inertia)
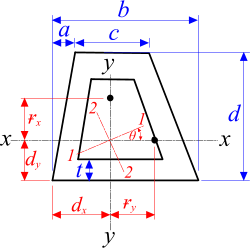
Fig 1. Typical Hollow Quadrilateral
The second moment of area (moment of inertia) and radius of gyration (also called second area moments) of any shape are properties that define its structural rigidity (ability to withstand deformation) about a given axis.
Polar Moment of Inertia
The second moment of area of any shape about any axis plus the second moment of area at right-angles to it will be equal to the sum of any other two second moments of area at right-angles to each other in the same plane. This sum of area moments is called the 'polar moment of inertia' of the shape.
The polar moment of inertia of a shape describes its ability to withstand torsional deformation (twist).
You can add Ixx and Iyy or I₁₁ and I₂₂, the result (the polar moment of inertia) should be the same in both cases.
Strong and Weak Axes
The second moment of area about the principal axes (Ixx & Iyy, Fig 1) of a regular shape (rectangle, I-Beam, circular tube, etc.) normally refers to its maximum and minimum structural planes of rigidity.
If the shape is asymmetrical, however, either the strongest or weakest axis will be about I₁₁ or I₂₂ (Fig 1) both of which are rotated anti-clockwise through θ
The area moments calculator also calculates the orientation of I₁₁ or I₂₂ axes to enable you to get the most from your section.
Radius of Gyration
The radii calculated in this second moment of area calculator are only valid for the shapes constructed. They cannot be simply added or subtracted for complex shapes. E.g. the radii of gyration (ɍx and ɍy) for a solid circle are both equal to 'R/2' whilst ɍx and ɍy for a hollow circular tube are equal to: ½√(R²+r²)
The radius of gyration can be found for any shape with the simple formula: √(I/A).
Second Moment of Area Calculator - Technical Help
Solid Shapes
Set the wall thickness ('t') to zero to calculate the properties of a solid shape using Area Moments
Note, this does not actually calculate the properties of a shape with zero wall thickness. It is simply a facility to enable you to calculate the properties of a solid shape.
Hollow Shapes
The cross sectional area of any body is the area of solid material on the face exposed after the body has been cut through (excluding all hollow areas) and which, when multiplied by the length of a bar or beam of constant cross-section will give you its volume.
Whilst the internal second moment of area may be subtracted from external second moment of area to find 'I' (about a common axis) for regular hollow shapes such as rectangular or circular tubes, this is not the case for irregular, skewed or complex shapes (e.g. triangles, sectors, non-constant wall thickness, etc.). If you have non-centralised hollow shapes you cannot simply add or subtract values, you need to sum their moments using; I=y².∫dA & I=I+y².A
Complex Shapes
You may use CalQlata's Area Moments+ calculator for complex shapes such as a physically connected group of rectangles, triangles elipses, etc. positioned irregularly.
Self-Check
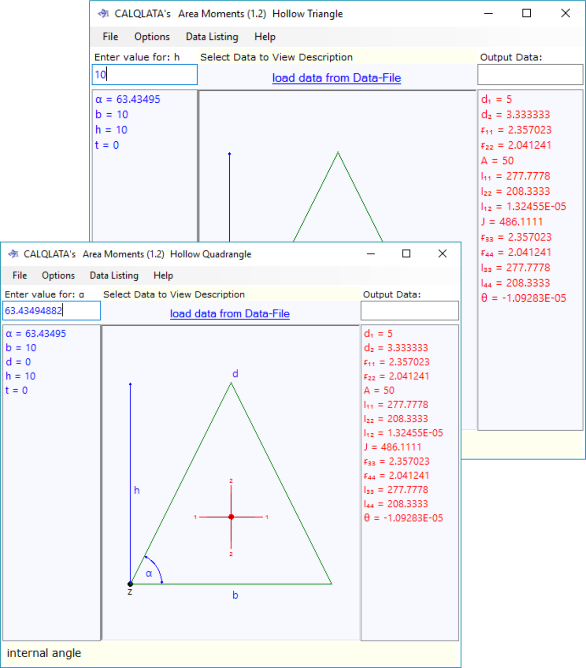
As Area Moments uses a single (and different) complex formula for each calculation option, if it correctly predicts the simple results, it can be assumed that the more complex configurations should also be accurate. Moreover, because the procedures are different in each calculation option, you can establish the accuracy of this calculator (apart from carrying out your own hand calculations) by comparing results from the various options (Fig 2).
Hollow Triangle
Any triangle may be generated so long as the base ('b') is at the bottom. You may cross-check this calculation option with 'Hollow Quadrangle' should you wish to do so. Enter a triangle with the dimensions: a;5, b;10, d;10, t;0 and compare the result with the example provided in 'Hollow Quadrangle' below. Copy the data listings into your spreadsheet, you should see the same outputs.
Hollow Quadrangle
You may create any quadrilateral or solid triangle you wish, even an inverted triangle if you set the base ('b') to zero and cap ('c') > zero. You may cross-check this calculation option with 'Hollow Triangle' should you wish to do so. Enter a quadrilateral with the dimensions: a;5, b;10, c;0, d;10, t;0 and compare the result with the example provided in 'Hollow Triangle' above. Copy the data listings into your spreadsheet, you should see the same outputs. Note: you cannot produce hollow triangles with this calculation option.
Polygon
Polygons may be generated with any number of sides. You may cross-check these calculations with 'Ellipse' and 'Sector' by generating a polygon with over a thousand sides and comparing the outputs with the examples provided in 'Ellipse' and 'Sector'. Cross-checking example: Set n;1000 and r;10
You can also cross-check 'Polygons' (n;3 & r;2.8868) with 'Hollow Triangles' (a;5, b;10, d;8.6603 & t;0) and 'Polygons' (n;4 & r;5) with 'Hollow Quadrangles' (a;0, b;10, c;10 d;10 & t;0). Note: 'dy' will not necessarily be the same in Triangles and Quadrangles, as this dimension may be to a different corner in the Polygon calculation.
Ellipse
A true ellipse within a true ellipse will not give a constant wall thickness so only solid shapes are calculated. You may use 'Sector' to calculate the properties of hollow circular sections. However, as the centre-of-areas of two coincident ellipses are in the same place you may simply add or subtract their areas and second moments of area (see Radius of Gyration above). Cross-checking example (with Polygons - above): Set a;10 and b;10
Sector
You may calculate the properties of any part of a solid or tubular circle using this option. The properties of a complete tube (or circle) can be found by setting 'α' to 180. To verify this calculation option, you may cross-check its results with 'Polygon' and 'Ellipse'. Cross-checking example: Set α;180, r;0 and R;10
Units
You may use any units you like, but you must be consistent.
Further Reading
You will find further reading on this subject in reference publications(2, 3 & 4)

