Work, Energy, Power, Torque, etc. (relationships)

{units} are provided for information only
The following relationships apply to any and all consistent units, both metric and Imperial
The symbol ᶜ refers to radians

Linear:

Momentum (p) = m.a.t = m.v {kg.m/s}

Force (F) = m.a {kg.m/s²}

Energy (U) = F.d = m.a.d {kg.m/s² . m}

Potential Energy (Uᴾ) = m.a.d {kg.m²/s²}

Kinetic Energy (Uᴷ) = ½.m.v² {kg.m²/s²}

Deformation Energy (Uᴰ) = ½.m.a.y {kg.m/s² . m}

Work (W) = Energy {kg.m²/s²}

Power (P) = m.a.d / t {kg.m/s² . m / s}

Energy = Work = Power . t = Momentum . v

Where:
m = mass {kg}
a = acceleration {m/s²}
d = distance {m}
y = deformation {m}
v = velocity {m/s}
t = time {s}

Rotary:

Inertia (I) = ⅖.m.R² {kg.m²}

Torque (T) = m.α.R² {kg . ᶜ/s² . m²}

Energy = ½.I.ω² = ½ . ⅖.m.R² . ω² = ½ .⅖ . m.(ω.R)² [= ⅕.m.v²] {kg . ᶜ²/s² . m²}

Work = 2π.T {ᶜ . kg.m²/s²}

Power = 2π.N.T = ω.T {ᶜ/s . kg.m²/s²}

Energy = 2π . Work = 2π.t . Power = (2π)² . Torque

Where:
m = mass {kg}
α = angular acceleration (ᶜ/s²)
R = radius {m}
v = rotational velocity at the surface of the mass {m/s}
ω = angular velocity {ᶜ/s}
t = time {s}
2π.t = angular period {ᶜ.s}

Orbital Power:

The power of a satellite is a measure of its ability to overcome the potential force between it and its force-centre, which can be established from its coincidental orbital velocity:
P = force x velocity {kg.m/s² . m/s = kg.m²/s³ = kg.m²/s² / s = J/s = W}
This means that whilst a satellite's energy is constant throughout its orbit, its power will vary.

Everything is Energy

The entire universe comprises just two particles; electrons and protons, every one of which is a packet of electro-magnetic charge that radiates a static field throughout the universe. Both charges are of equal magnitude in the lone particle, but as they accumulate, magnetic interaction accrues (increases) and electrical interaction is shared (decreases).
Rotate a negatively charged electron about a positively charged proton (proton-electron pair) and they will generate an electro-magnetic field and radiate EME; just like a motor or generator.

Historically, we have thought about the interaction between particles in terms of force (F), which is why the distance (R) between bodies in Newton's formula is squared;
F = G.m₁.m₂/R² {N = kg.m/s²}; where m₁ and m₂ are masses of accumulated particles.

This is the reason we've been taught that potential force (what we today refer to as gravity) diminishes with the square of the distance from the source, which isn't strictly true. In reality this force is constant throughout the universe, but it is distributed over the spherical area at that distance.
However, if we treat this radiation as energy (E), the interaction between bodies at a distance becomes clearer;
E = G.m₁.m₂/R {J = kg.m²/s²}
energy is actually interaction dependent upon distance (not distance squared), such as torque and moments. So, it is natural to expect potential energy to vary with distance. But Isaac Newton wasn't aware of the concept of energy, it would not be discussed mathematically for another century.

In fact, everything in the universe is electro-magnetic charge, and their interaction is electro-magnetic energy. Everything we do is simply a measure of energy expenditure, and the rate at which we do it tells us the power needed. For example:

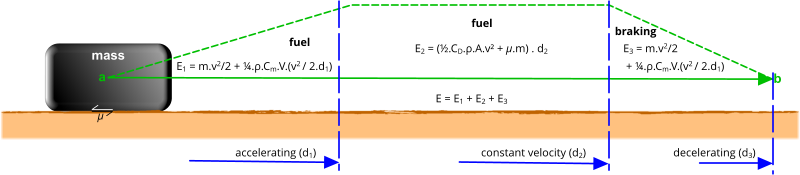
You can determine the energy required to move a mass from 'a' to 'b' by calculating potential energy during acceleration and deceleration, plus the energy (force times distance) required to overcome frictional resistance, along with added mass and drag when moving at a constant velocity through the atmosphere. The answer you're looking for will be in Joules (Fig 1).

Exactly the same applies to the addition or removal of heat. Every proton-electron pair in every atom is consuming and radiating EME; heat. All we need to do is multiply the specific heat capacity of the various elements involved by their masses, together with the temperature difference, and we will get the answer in Joules (Fig 2).

And if you want to calculate electrical energy, you can do this from the potential energy in the atom's outermost (shell) electron velocity (DC), or from the EME generated by the innermost electron shells (AC), multiplied by the number of atoms involved (Fig 3).

Divide this energy by the time over which it is to be achieved and you have the power.

Nature itself provides us with eternal energy in all of its neutrons. Therefore, it is much more efficient to utilise this free, natural energy directly than to use energy that has been generated and converted in various stages. Every time you introduce a new energy generation stage before its use, you reduce efficiency. This is why petrol in our cars is so much more efficient than the use of electricity from batteries, because energy from petrol is direct utilisation.

Further Reading

You will find further reading on this subject in reference publications^{(1, 2, 3 & 4)}