Elliptic Curves Calculator
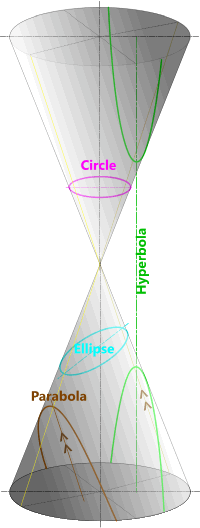
Fig 1. Conic Ellipses
The best known practical example of an ellipse is Johannes Kepler’s law for planetary orbits, the size and shape (eccentricity) of which are defined by the gravitational attraction between a planet and its sun.
Elliptical Family of Curves
Each curve in the family of ellipses (Fig 1; i.e. the circle, the ellipse, the parabola and the hyperbola) is called a conic because it is defined by the angle it cuts through a circular cone (or nappe).
Every conic (curve) is defined by the same equation:
ax² + bxy + cy² + dx + ey + f = 0
where a, b, c, d, e & f are the variables that define the type of curve (circle, ellipse, parabola or hyperbola)
Note: For all circles; a = 1, b = 0, c = 1
You can solve the above equation using determinants,
The determinant (δ) for the above equation is calculated thus;
δ = |2a, b, d|
|b, 2c, e|
|d, e, 2f|
δ = 2a.(2c.2f - e.e) - b.(b.2f - e.d) + d.(b.e - 2c.d)
for example;
3x² + 4xy - 2y² + 3x - 2y + 7 = 0
δ = |6, 4, 3|
|4,-4,-2|
|3,-2,14|
δ = 6x(-4x14 - -2x-2) - 4x(4x14 - -2x3) + 3x(4x-2 - -4x3)
δ = -596
b² - 4.a.c = 4² - 4x3x-2 = 40
a.c = 3x-2 = -6
a.δ = 3x-596 = -1788
as δ ≠ 0 and b² - 4.a.c > 0 the curve is an hyperbola ....
.... which can be deduced from the following table:
| b² - 4.a.c < 0 | b² - 4.a.c = 0 | b² - 4.a.c > 0 | |
|---|---|---|---|
| δ ≠ 0 | a.δ < 0: a ≠ c: ellipse a = c: circle a.δ > 0: no locus |
parabola | hyperbola |
| δ = 0 | point | n = d²+e²-4.f.(a+c) n<0: no locus n=0: one straight line n>0: two parallel straight lines |
two intersecting straight lines |
The shape of each conic is defined by its eccentricity (e), i.e. the ratio of the distances from any point (P) on the curve to its focus (F) and its directrix;
circle: R:r=0 (Fig 2)
parabola: r:r=1 (Fig 3)
hyperbola: r₁:r>1 (Fig 4)
ellipse: r₁:r<1 (Fig 5)
Half the width of the curve at the focus (F or F₁ or F₂) is called its parameter (p) or ordinate and is dependent upon the angle (or slope) of the cone.
The distance from the focus to the directrix of all the elliptical curves = p/e
The mathematical properties and relationships of these elliptical curves are defined below:
Circle
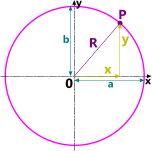
Fig 2. The Circle
Put a stake in the ground, slip a length of rope over it and pull it tight. Walk the other end through 360° and there you have it; a circle.
Cut a section through any right-circular cone normal to its axis (parallel to its base) and the circumference is a circle. Note: a cylinder is simply a cone with its slope parallel to its axis.
A circle is an ellipse (Figs 2 & 5) with identical semi-axes (a = b = R)
y = (R² - x²)⁰˙⁵
p = b = a = R
e = √(1 - [b/a]²) = 0
ƒ = a.(1 - e) = a
The distance from the focus to its directrix = a/e = ∞
Parabola
A parabolic curve is generated by the perimeter of a section cut through a cone parallel to its slope (Fig 1).
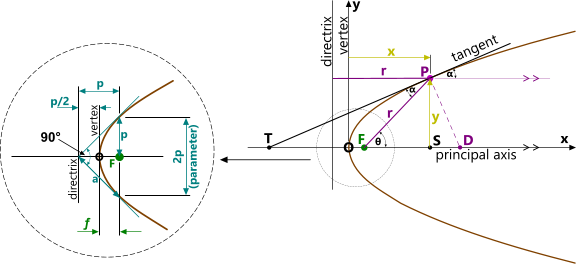
The definition of a parabola is a locus generated by a point (P) of equal distance (r) to a fixed line called its directrix and a fixed point called its focus.
y = (2.p.x)⁰˙⁵
p = a/√2
e = 1
ƒ = a / 2¹˙⁵
r = p / (1-Cos(θ))
The distance from the focus to its directrix = p = 2.ƒ
A beam of light emitted from focus 'F' to point P will reflect in a direction parallel to the principal axis. I.e. equal and opposite angles α will always result in a path parallel to the principal axis for any point P on the curve.
Hyperbola
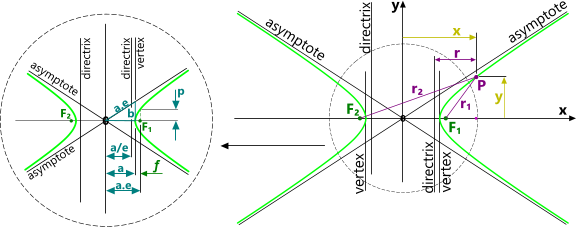
Two hyperbolic curves are generated by the perimeters of a section through two nappes (of a cone) parallel to their axes (Fig 1). Both foci (F₁ & F₂) are a.e from the joined apexes (or apices) of the two nappes (the origin, where x = 0)
Either of the following constitutes a definition of the hyperbola:
1) r₂ - r₁ = 2a where 2a is the distance between vertices
2) r₁ ÷ r = e
y = b/a . (x² - a²)⁰˙⁵
p = a.(e² - 1)
e = (1 + [b/a]² )⁰˙⁵ and is greater than 1
ƒ = a.(e - 1)
r = p / (1-e.Cos(θ)) = r₁/e
The distance from the focus to its directrix = a.(e - 1/e)
Ellipse
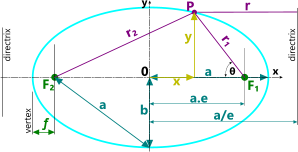
Fig 5. The Ellipse
Tilt a circle and you will see an ellipse. All the shapes discussed on this page (circle, ellipse, parabola & hyperbola) are special variations of an ellipse.
An ellipse is generated by the perimeter of a section through a cone at any angle (Fig 1).
A complete ellipse only occurs if its entire circumference cuts the slope of the cone.
A projection drawing (Fig 7) is provided for those finding it difficult to understand how a slanted section through a cone (with sloping sides) can produce a symmetrical ellipse.
y = b/a . (a² - x²)⁰˙⁵
p = a.(1 - e²)
e = (1 - [b/a]² )⁰˙⁵ and is less than 1
ƒ = a.(1 - e)
r = a.(1/e-e) + r₁.Cos(θ) = r₁/e
The distance from the focus to its directrix = a.(1/e - e)
The Tangent of an Elliptical Curve
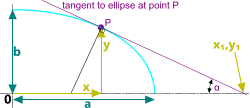
Fig 6. Tangent of a Curve
The usual formula for the tangent of a point (P) on an elliptical curve is:
b².x.x₁ + a².y.y₁ = a².b²
In which case you need to know both x₁ and y₁ to solve the problem
The most important thing to find is the angle of the tangent (α),
which is easier if you follow the diagram in Fig 6, therefore setting y₁ to zero
In this case; b².x.x₁ + a².y.y₁ = a².b²
or
x₁ = a²/x
and
α = Atan(y / [x₁-x])
Ellipse Calculator - Technical Help
There are no unit constraints for this calculator, you simply get out what you put in.
The Ellipse
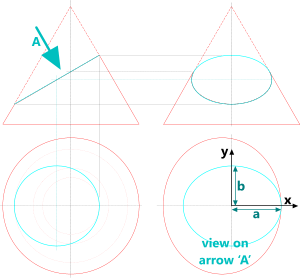
Fig 7. Construction Drawings of a Conical Ellipse
All properties are calculated for any point (x,y) on the quarter of an ellipse bounded by centre co-ordinate '0,0' and positive values for 'x' and 'y' (see Fig 5)
The value of ‘x’ must be greater than or equal to ‘0’ and less than ‘a’
This calculation only works if ‘a’ (x-axis) is greater than ‘b’ (y-axis), i.e. the ellipse is always flattened vertically. Ellipses will display a warning if you enter a value for ‘a’ less than ‘b’.
The Hyperbola
All properties are calculated for any point (x,y) on the positive quarter of an hyperbola bounded by co-ordinate 'a,0' and positive values for 'x' and 'y' (see Fig 4)
This calculation only works if ‘x’ is greater than ‘a’. Ellipses will display a warning if you enter a smaller value for ‘x’ than for ‘a’.
The Parabola
All properties are calculated for any point (x,y) on the positive quarter of a parabola bounded by co-ordinate '0,0' and positive values for 'x' and 'y' (see Fig 3)
Input Data
x = the horizontal distance along the x-axis to point 'P' on the curve
a = the horizontal aspect dimension used in the definition of the curve’s eccentricity (e) and its parameter (p)
b = the vertical aspect dimension used in the definition of the curve’s eccentricity (e) and its parameter (p) {does not apply to the parabola}
p = the curve parameter used to define its width
nº = the number of co-ordinates in the plot-list generated by the ellipse calculator
In order to minimise calculation times, you should set nº to 10 until you have achieved the results you need, then increase this value to that required.
Output Data
y = the vertical distance along the y-axis to point ‘P’ on the curve
e = the eccentricity of the curve
a = the horizontal aspect dimension used in the definition of the curve’s eccentricity (e) and its parameter (p)
b = the vertical aspect dimension used in the definition of the curve’s eccentricity (e) and its parameter (p) {does not apply to the parabola}
ƒ = the distance along the x-axis from the vertex to the focal point (F)
r = the distance along the x-axis from the directrix to point 'P' on the curve (and the distance from the focal point (F) to the same point 'P' a parabolic curve)
r₁ = (ellipse and hyperbola) the distance from focal point 1 (F₁) to point 'P' on the curve
r₂ = (ellipse and hyperbola) the distance from focal point 2 (F₂) to point 'P' on the curve
R = the radius of the curve at point 'P'
ℓ = the arc length of the curve from …
Ellipse: '0,b' to point 'P' on the curve
Hyperbola: 'a,0' to point 'P' on the curve
Parabola: '0,0' to point 'P' on the curve
A = the area under the curve from …
Ellipse: '0,b' to 'x,0'
Hyperbola: 'a,0' to 'x,y'
Parabola: '0,0' to 'x,y'
Arc Length
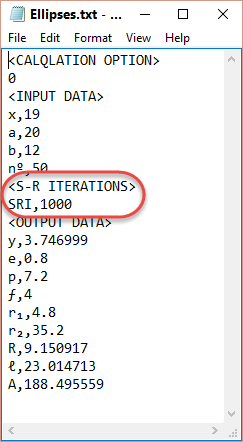
Fig 8. Simpson's Rule Iteration (SRI)
Arc lengths for the Ellipse and Hyperbola are calculated using Simpson’s Rule, therefore the smaller δx (or the greater the number of iterations) the more accurate the result (see Ellipse and Hyperbola below).
The ellipse calculator defaults the number of iterations (Fig 8: SRI) to 1000 which is virtually instant for today’s computers. You may, however, modify this value by opening the ellipse calculator’s Data File (Menu Item; ‘File>Open Data File’), edit the value, taking care not to delete the preceding comma, then save the file. You can then upload the saved data (in the Data File) into the ellipse calculator via Menu Items; ‘File>Load Data’ or ‘File>Quick Load’.
Ellipses limits the number of iterations (SRI) to 10000000 in order to minimise slowing down the calculation excessively.
You must also ensure that the SRI value being used is sufficient to provide the required accuracy, for example; if you enter a value for ‘x’ of 19.999 and 20 for ‘a’ in the ELLIPSE calculation option, you will need an SRI value greater than 1000 (i.e. 1/0.001) to achieve a result.
Ellipse
The expected accuracy of a typical arc length calculation for an ellipse (x;15, a;20, b;12) dependent upon ‘SRI’ is shown below:
SRI: ℓ
25: 15.522424
50: 15.760835
100: 15.760835
As ‘x’ gets closer to ‘a’ (x→a) (e.g. ‘a=x') you will need to increase the SRI value to obtain greatest levels of accuracy, e.g. for the above ellipse (x;20, a;20, b;12):
SRI: ℓ
100: 25.526714
1000: 25.528125
10000: 25.527392
1000000: 25.527039
Note: The correct answer is always slightly less than the value predicted using the highest SRI, i.e. the actual result for the above example is slightly less than 25.527039
There are a number of approximate formulas for the perimeter of an ellipse, some of which offer excellent levels of accuracy.
A typical discrepancy for the above ellipse ‘x;20, a;20, b;12’ is shown below:
Using an approximate formula {ℓ = ¼π . ( 2.(a²+b²) – (a-b)²/2.2 )⁰˙⁵}: ℓ = 25.55755004
Compared with a more accurate value of 25.527039
Hyperbola
The expected accuracy of a typical arc length calculation for an hyperbola (x;31, a;20, p;7.2) dependent upon ‘SRI’ is shown below:
SRI: ℓ
50: 18.507058
100: 18.512783
1000: 18.513683
10000: 18.51311
1000000: 18.512847
10000000: 18.512847
Parabola
The result for a parabolic arc length is not iterative, it is exact. The SRI constant has no effect on this calculation.
Applicability
Ellipses applies to all calculations associated with the properties of elliptical curves; i.e. the ellipse, the hyperbola and the parabola
Accuracy
All output data from the ellipse calculator is accurate, except for the arc length of the hyperbola and the ellipse, both of which should be within ±1E-06 provided the correct iteration value (SRI) is used
Further Reading
You will find further reading on this subject in reference publications(3, 12, 14 & 19)

