Mohr's Circle (a calculation method)
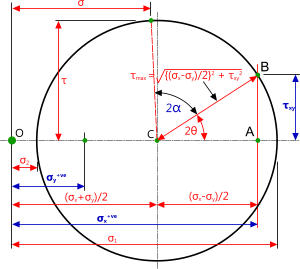
Fig 1. Mohr's Circle (σ⁺ᵛᵉ & σ⁺ᵛᵉ)
Combined Stresses such as 'Principal' and 'Equivalent' are used in fatigue calculations and limiting design criteria in any stressed body (see CalQlata's Combined Stress and Fatigue calculators).
Mohr's circle uses a trigonometric method for calculating 2-D equivalent and principal stresses in a body exposed to two-dimensional elastic stresses. This method was developed by a German engineer (Otto Mohr) in the late 19th century.
Figs 1 & 2 show the diagram he developed for this calculation; Fig 1 is for both primary stresses positive or negative and Fig 2 is for one positive and one negative stress.
Where:
σx is the primary stress in the x direction that you will need as input data for your calculation, along with; the primary stress σy in the y direction (90° to σx)⁽¹⁾ and the shear stress τxy in the same plane as σx and σy
α is the angle of rotation (anticlockwise rotation shown) of a plane for which you require tensile and shear stresses (σ and τ)⁽³⁾
With the above input data you can calculate the following:
The line 'C-B' represents the plane of your stressed point. Therefore, if your stressed plane is vertical, you should rotate your Mohr's circle (and everything in the diagram) so that this line is vertical
σ1 is the principal stress in the x direction
(σx rotated in the same plane through θ° as a result of τxy)⁽²⁾
σ2 is the principal stress in the y direction
(σy rotated in the same plane through θ° as a result of τxy)⁽²⁾
θ is the angle of rotation of both σx and σy into their principal stresses from line 'C-B' (i.e. clockwise)⁽³⁾
τmax is the maximum shear stress in this two dimensional plane
σ is the tensile stress in the two dimensional plane α
τ is the shear stress in the two dimensional plane α
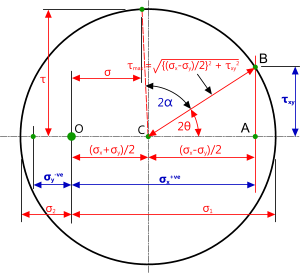
Fig 2. Mohr's Circle (σ⁺ᵛᵉ & σˉᵛᵉ)
Example Calculation
Input Data:
σx = 235, σy = -116, τxy = 97 & α = 35°
Calculate:
(σx-σy)/2: (235 - -116)/2 = 175.5
(σx+σy)/2: (235 + -116)/2 = 59.5
Note: 175.5 + 59.5 = 235 (i.e. the magnitude of σx)
Draw a horizontal line representing a length of 175.5 out from the centre (Point 'C') of what will become your circle to Point 'A'
Draw another horizontal line representing a length of 59.5 out to the left of the centre of your circle to Point 'O'
Draw a vertical line representing a length of 97 up from Point 'A' to Point 'B'
The radius of your circle is the hypotenuse of the triangle 'C-A-B', which is also the maximum shearing stress in this plane (τmax = 200.5224)
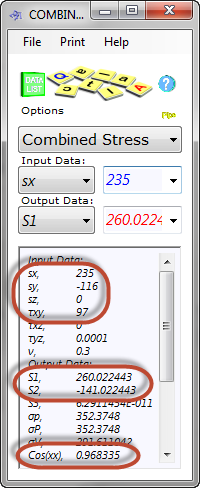
Fig 3. Combined Stress
Principal Stress σ1 is the distance from Point 'O' to the circumference of your circle beyond 'A'
(59.5 + 200.5224 = 260.0224)
Principal Stress σ2 is the distance from Point 'O' to the circumference of your circle in the opposite direction
(-200.5224 + 59.5 = -141.0224)
θ = Atan(97 / 175.5)/2 = 14.46485821°
the Cosine of which is the
angle cosine of σx about the x-axis
(see Principal Stress Calculator below)
σ = 59.5 + 200.5224 x Cos(70°+28.93°)⁽³⁾ = 28.37
τ = 200.5224 x Sin(70°+28.93°)⁽³⁾ = 198.092
Principal Stress Calculator
CalQlata's Combined Stress calculator will determine the principal stresses and their cosine values for you, albeit the program does not use Mohr's circle formulas to do so hence the small difference between the Cosine results.
The results from the combined stress calculator in Fig 3 are for the example calculation above.
The Cosine value of 0.968335 = 14.45821075°
Notes
- σx and σy are always at 90° to each other
- σ1 and σ2 are always at 90° to each other
- All actual angles in Mohr's circle are doubled pictorially and also for calculation