Rotary Balance Calculator (for wheels and shafts)
If a rotating body such as a gear-wheel or drive-shaft is totally uniform in material and construction for 360°, all opposing centrifugal forces (Fc) anywhere within the body will be equal.
If a mass (m₁) is located at a fixed radius (r₁) anywhere on this body, a different mass (m₂) must also be added to the body, 180° to m₁, at radius r₂ according to the relationship; r₂ = r₁.m₂/m₁
A problem arises, however, if the body features multiple mass anomalies (m₁, m₂, m₃, m₄, … mᵢ) in which case it would be necessary to find an equivalent single mass, along with its position, that will counterbalance their combined effect.
Rotating Disc
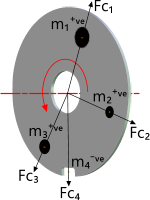
Fig 1. Unbalanced Disc
For example, the model described in Fig 1 shows a disc (or wheel) with three positive masses and one negative mass at known but random locations. It should be noted that the positive masses (m₁, m₂ & m₃) are shown as insets within the disc structure and as such must be calculated as mass differentials; i.e. the difference between the mass of the inset and the mass of the disc material removed to allow fitting. Whereas m₄ is a mass of material removed from the disc and therefore must be treated as a negative value. The radial location of each mass is from the axis of rotation to each CofG and all angles are measured from a common datum. Unless all these masses are deliberately and accurately located to ensure balance, the disc will vibrate and if it is allowed to resonate⁽¹⁾ this vibration could cause the disc to shatter prematurely due to excessive localised centrifugal force differentials and internal stresses.
The combination of all these masses can be replaced with a single equivalent force vector (i.e. a directional centrifugal force; Fcₑ)
The solution to this problem is to identify a single additional mass and its position that will counterbalance Fcₑ. The magnitude of this mass will depend upon the radial location according to the relationship r = m.v²/Fc and its angular orientation must be 180° to Fcₑ
It doesn’t matter how irregular its shape, if all the opposing centrifugal forces in a rotating body are equal it will not vibrate.
Rotating Shaft
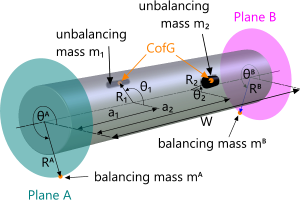
Fig 2. Unbalanced Shaft
The solution to an unbalanced shaft is similar to that of a disc, however, because these unbalancing masses can be located anywhere along the length of a shaft, the problem becomes one in 3-D. That is, masses placed at various positions along the length of the shaft will induce a longitudinal moment couple from the various unequal centrifugal forces.
It therefore becomes necessary, in such a case, to incorporate two balancing masses at different positions along the shaft that will generate an equal and opposite moment couple. The further apart these masses are located the smaller they will be.
For example, the shaft in Fig 2 shows two unbalancing masses (m₁ & m₂) located at distances a₁ & a₂ from plane A and on which the balancing masses (mᴬ & mᴮ) will be fixed at both ends of the shaft (Planes A & B).
If the balancing masses (mᴬ & mᴮ) are correctly sized and located the shaft will be stabilised centrifugally and longitudinally; i.e. no vibration.
Balancing Calculator – Technical Help
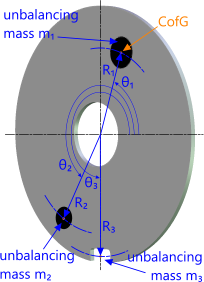
Fig 3. Balancing a Rotary Disc
Units
You may use any units you like, but you must be consistent.
Example Calculation for a Disc (1-Plane)
A 0.012m thick aluminium disc of diameter 0.5m (Fig 3) is fitted with two tungsten inserts (m₁ & m₂) flush to both faces of the disc, and one cut-out (m₃)
m₁: Ø₁ = 0.05m; R₁ = 0.179m; θ₁ = 70°
m₂: Ø₂ = 0.035m; R₂ = 0.214m; θ₂ = 240°
m₃: A₃ = 0.03m x 0.2m; R₃ = 0.24m; θ₃ = 270°
Note: δm = π.ز.t.(ρᵂ - ρᴬˡ)/4
m₁ = π x 0.05² x 0.012 x (19293 - 2713) / 4 = 0.390657 kg
m₂ = π x 0.035² x 0.012 x (19293 - 2713) / 4 = 0.191422 kg
m₃ = -0.03 x 0.2 x 0.012 x 2713 = -0.19534 kg
The balancing mass is to be placed at radius (R) = 0.245m;
The balancing mass (m) = 0.315071 kg (Fig 4)
and must be located (θ) = 267.449909° from the common datum
Calculation for a Shaft (2-Planes)
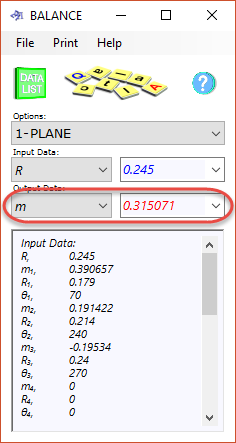
Fig 4. Calculation Example
A shaft is calculated in exactly the same manner a disc with the following additional inputs:
W: The distance between the planes (A & B) in which the two balancing masses (mᴬ & mᴮ) must be located.
These planes can be anywhere along the shaft you like as long as they are normal to the axis of rotation.
a₁ to a₁₀: Are the distances of each unbalancing mass (m₁ to m₁₀) from Plane A (Fig 2)
Rᴬ and Rᴮ: Are the radial locations of balancing masses (mᴬ & mᴮ) within Planes A & B respectively
θᴬ and θᴮ: Are the angular locations of balancing masses (mᴬ & mᴮ) within Planes A & B respectively
Assembly Calculations
Disc and shaft assemblies should be balanced separately. I.e. you balance the disc as a separate entity and then balance the shaft, as described above.
Applicability
Balancing applies to any rotating shape, including; wheels discs, all shafts (cam, crank, plain, drive, etc.).
Accuracy
There is no error margin in these calculations; i.e. the output data is as accurate as the input data
Notes
- 1) A perfectly balanced disc has no natural frequency and therefore cannot resonate (see Vibration Damping)
Further Reading
You will find further reading on this subject in reference publications(2)

