Steel Beams
(I-Beam H-Beam Channel Angle RHS THS SHS)
Whilst this calculator is for steel beam dimensions, apart from the weight (per unit length), all the properties provided here are equally valid for the same sections manufactured from any material.
Section Designation (e.g. 14x176)
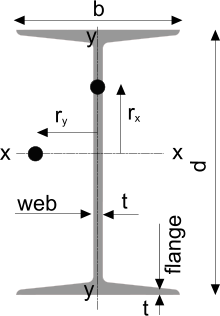
Fig 1. Typical 'Steel Beam Sizes'
Dimensions & Symbols
This Designation is a name for the beam size that varies according to the section type.
H-Beam, I-Beam & Channel: Depth [in] x Weight [lb/ft]
Angle: Leg length [in] x Leg length [in] x Thickness [in]
RHS (Rolled Hollow Section): Depth [mm] x Width [mm] x Wall Thickness [mm]
SHS (Square Hollow Section): Depth [mm] x Width [mm] x Wall Thickness [mm]
THS (Tubular Hollow Section): Diameter [mm] x Wall Thickness [mm]
Beam Weight Per Unit Length
This value is extracted from the 'Designation' for standard forged steel beam sizes such as: H-Beams, I-Beams and Channel [lb/ft]. It is calculated for Angle [lb/ft] and RHS & THS [kg/m]
Beam Cross Section Area
The values included in this table are from a recognised source and checked by calculation. They include the effects of the taper and the fillet radii.
Beam Depth
The depth ('d' see Fig 1) of the section is as dimensioned ('d') in the illustration associated with each section within the calculator.
Beam Width
The width ('b' see Fig 1) of the section is as dimensioned ('b') in the illustration associated with each section within the calculator.
Beam Flange Thickness
The thickness of the horizontal member of the section (flange 't' see Fig 1). I-Beam, Channel and Angle flanges are tapered. That is, they vary in thickness across their length. The thickness specified in this calculator for these sections is the average thickness (mid-length).
Beam Web Thickness
The thickness of the vertical member of the section (web 't' see Fig 1). These sections are always strongest if used with the load acting parallel to the Web. Angle and RHS Webs are the longest sides.
Beam Second Moment of Area (x-x & z-z)
The second moment of area of all these sections are about their centre of area.
Beam: Section Modulus (x-x & y-y)
Sometimes called the elastic modulus, the section modulus is the ratio of second moment of area to the distance from the centre of area (neutral axis) to the extreme edge (fibre) of the section (also equal to Bending Moment divided by Stress in the extreme fibre).
Beam: Radius of Gyration (x & y)
The distance from the neutral axis (x-x or y-y) to the centre of the area (mass) either side of it ('ɍx' and 'ɍy' see Fig 1).
Beam: Polar Moment of Inertia
The section's resistance to rotational twist is equal to the sum of any two 'second moments of area' at 90° to each other.
Beam: Distance to Centre of Area (x & y)
The horizontal and vertical distances from the bottom left-hand corner of the section to the centre of area of the section.
Steel Beam Sizes - Technical Help
Applicability
This database applies to all standard forged steel beams with the associated designation
Accuracy
The information in this this database is derived from the data in the associated designation (dimensions) and the density of carbon steel. Therefore, whilst there may be slight differences between 'Steel Beam Sizes' and other tables or databases this one should be as correct as the designation.
Further Reading
You will find further reading on this subject in reference publications(2 & 3)

