Resolution of Forces Calculator
(equivalent single force)
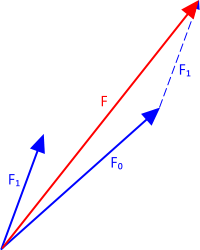
Fig 1. Resolution of Forces
The "resolution of forces" is the determination of a single equivalent force applied at a given point that results in exactly the same loading condition as a collection of individual forces applied at the same point. Fig 1 shows two typical individual forces; 'F₀' & 'F₁' and the resolved (equivalent) force 'F', can be established using triangulation.
Whilst the resolution of just two forces is relatively straightforward, the problem becomes tedious and prone to error when more than two forces are involved and/or they are applied in 3-D (Fig 2).
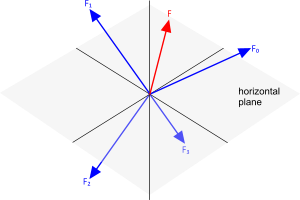
Fig 2. Resolution of Forces
Moreover, the potential error problem can be exacerbated with complex co-ordinate systems both from the point of view of translation into useable input data and understanding of the output results. For example, a Cartesian co-ordinate system based upon x,y,z components for each force, would complicate the generation of input data increasing the likelihood of errors. CalQlata prefers to use a modified version of the Polar co-ordinate system (see Co-ordinate System below), thereby reducing input angles to just two (α & β) and/or simplifying input data estimation if an estimate is acceptable.
Where the forces to be resolved do not all pass through exactly the same point, whilst the same equivalent force will apply, bending moments, shear forces and torsion will occur across these forces at the anchor. In such an event, separate calculations will be required to establish resultant local stresses at the anchor.
Resolution of Forces Calculator - Technical Help
Units
You may use any units you like, but you must be consistent.
Co-ordinate System

Fig 3. Co-ordinate System
Some 3-D co-ordinate systems can be confusing and/or complicated, increasing the possibility of errors. As such, this resolution of forces calculator does not allow for 360° of rotation for every individual force in every direction. The co-ordinate system used by this calculator allows you to enter an angle in the horizontal plane about a vertical axis (α) between -180° and 180° and the angle in the vertical plane (β) between -90° and 90°, giving you full 360° capability in all directions with only two inputs and minimal complexity (Fig 3).
Input Data
A typical example for the orientation of a force (α & β) is shown in Fig 4 where you first orientate each input force (F) in the horizontal plane (α, -ve example shown) and then orientate it vertically above or below the horizontal plane (β, +ve example shown).
Output Data
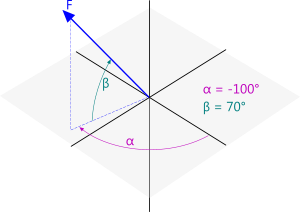
Fig 4. Entering Data
The output data (results) are provided in exactly the same co-ordinate system.
If the angle in the horizontal plane (α) is negative, the force is rotated in a clockwise direction (looking down from above). If it is positive, the force is rotated in an anti-clockwise direction.
If the angle in the vertical plane (β) is negative, the force is rotated downwards. If it is positive, the force is rotated upwards.
Accuracy
The output data is as accurate as the input data.
If you enter forces that are equal and opposite, i.e. they cancel each other out the resolution of forces calculator may show a result as "Infinity" along with an error message: "Result is zero or division by zero". Infinity is an automatic processor response and does not mean that you have generated an infinite equivalent force it simply means that the calculation encountered a division by zero.
Further Reading
You will find further reading on this subject in reference publications(2, 3 & 4)

