Hardness (measurement & conversion)
This page is not a universal hardness comparison facility for its own sake.
It is provided to help you compare hardness scales with a reasonable degree of confidence.
There are a number of hardness comparison calculation methods available in many publications the accuracy of which is variable and difficult to gauge without a good deal of verification work. CalQlata has therefore developed its own formulas⁽¹⁾ that it can use internally with confidence. These formulas and their accuracy can be found in the following Tables. Our aim was to keep errors within ±0.5% throughout the range although the variable nature of the documented data has made this a little challenging (see Shore below).
The following Tables include documented values, calculated {Q} values and associated errors for each set of formulas (see Comparison Charts at the bottom of this page).
CalQlata has included all the following conversion formulas in a hardness conversion calculator
Rockwell C (HRC)
CalQlata has compared the most commonly used hardness measurement systems with Rockwell 'C'#, which is regarded as the most ubiquitous hardness test method and its Grade C the most commonly used scale.
# except Rockwell 'B' which is compared with Brinell std.
Hugh and Stanley Rockwell together invented this hardness testing method in the USA in the mid 19th century, which involves no calculations and the hardness number is read from a dial or digital display. It is more accurate and less damaging than the Brinell method, simpler and quicker to operate than the Vickers method and more reliable than the Shore hardness test.
It has numerous measurement scales: A to G, 15, 30 & 45 and measures the depth of penetration of a diamond spherocone with tip diameter of 0.2mm and an included angle of 120° or a steel ball ranging in diameter from 1.5mm to 10mm all of which can be applied with a load ranging from 15kg to 3000kg.
The operational procedure is to apply an initial load of 10kg followed by the main test load which is held for 30 seconds. The hardness number is based upon the depth of penetration.
Vickers Hardness Number (HV)
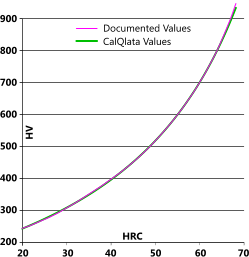
Rockwell C vs Vickers
This test, which was devised at Vickers Ltd. by Robert Smith and George Sandland is very accurate when compared with the Brinell and Rockwell methods and may be used on sheet material but the equipment is expensive and takes longer to operate accurately.
The Vickers test is based upon the indentation of a diamond pyramid, with an included peak angle of 136°, for a period of 30 seconds. The Vickers number (HV) is the ratio of the force (F) and the square of the depth of penetration (D). The applied force is 5, 10, 20, 30, 50 or 120kg; 50kg being the norm.
HV = F ÷ (0.5393 x d²)
where d is the diagonal length of the indentation.
| HRC | HV | HV {Q} | Error | Formulas |
|---|---|---|---|---|
| 68 | 940 | 927 | 1.4% | HV = (223xHRC+14500)÷(100-HRC) HRC = (100xHV-14500)÷(223+HV) |
| 67 | 900 | 892 | 0.9% | |
| 66 | 865 | 859 | 0.7% | |
| 65 | 832 | 828 | 0.4% | |
| 64 | 800 | 799 | 0.1% | |
| 63 | 772 | 772 | 0.1% | |
| 62 | 746 | 745 | 0.1% | |
| 61 | 720 | 721 | 0.1% | |
| 60 | 697 | 697 | 0.0% | |
| 59 | 674 | 675 | 0.1% | |
| 58 | 653 | 653 | 0.0% | |
| 57 | 633 | 633 | 0.0% | |
| 56 | 613 | 613 | 0.1% | |
| 55 | 595 | 595 | 0.0% | |
| 54 | 577 | 577 | 0.0% | |
| 53 | 560 | 560 | 0.0% | |
| 52 | 544 | 544 | 0.1% | |
| 51 | 528 | 528 | 0.0% | |
| 50 | 513 | 513 | 0.0% | |
| 49 | 498 | 499 | 0.1% | |
| 48 | 484 | 485 | 0.1% | |
| 47 | 471 | 471 | 0.1% | |
| 46 | 458 | 458 | 0.1% | |
| 45 | 446 | 446 | 0.0% | |
| 44 | 434 | 434 | 0.0% | |
| 43 | 423 | 423 | 0.1% | |
| 42 | 412 | 411 | 0.1% | |
| 41 | 402 | 401 | 0.3% | |
| 40 | 392 | 390 | 0.4% | |
| 39 | 382 | 380 | 0.5% | |
| 38 | 372 | 371 | 0.4% | |
| 37 | 363 | 361 | 0.5% | |
| 36 | 354 | 352 | 0.6% | |
| 35 | 345 | 343 | 0.5% | |
| 34 | 336 | 335 | 0.4% | |
| 33 | 327 | 326 | 0.2% | |
| 32 | 318 | 318 | 0.1% | |
| 31 | 310 | 310 | 0.1% | |
| 30 | 302 | 303 | 0.2% | |
| 29 | 294 | 295 | 0.4% | |
| 28 | 286 | 288 | 0.7% | |
| 27 | 279 | 281 | 0.8% | |
| 26 | 272 | 274 | 0.8% | |
| 25 | 266 | 268 | 0.6% | |
| 24 | 260 | 261 | 0.5% | |
| 23 | 254 | 255 | 0.4% | |
| 22 | 248 | 249 | 0.3% | |
| 21 | 243 | 243 | 0.1% | |
| 20 | 238 | 237 | 0.4% |
Brinell Hardness Number - std (BHN)
.png)
Rockwell C vs brinell (std)
A standard ball is used for the Brinell hardness test on materials with a BHN value of less than 450.
This test, which was devised by the Swedish engineer Dr Johan August Brinell is less accurate than the Vickers method but benefits from not actually requiring any special equipment so long as you can accurately measure the applied load, making it ideal for improvisation. However, the thickness of the test specimen must be greater than 10 times the depth of the indentation, which is not insignificant and cannot be regarded as non-destructive testing due to the size of the indentation produced.
The depth of indentation (d) is generated by applying a force 'F' to a hard steel sphere of diameter 'D' for a period of at least 15 seconds (30 seconds for nonferrous metals).
The Brinell hardness number (BHN) is calculated as follows:
BHN = F ÷ A
where A is the surface area of the indentation: A = ½.π.D x ( D - √[D²-d²] )
A certain amount of intelligence is required to use this method accurately in that insufficient and/or excessive depth of impression will result in misleading or inaccurate results. The optimum depth will be between 2.5 and 4.75mm for a standard 10mm ball.
The following table is based upon a 10mm diameter ball and a force of 3000kg
| HRC | BHN | BHN {Q} | Error | Formulas |
|---|---|---|---|---|
| 52 | 508 | 497 | 2.2% | BHN = 122+HRC1.5 HRC = 1.5√[BHN-122] |
| 51 | 494 | 486 | 1.6% | |
| 50 | 481 | 476 | 1.1% | |
| 49 | 469 | 465 | 0.9% | |
| 48 | 455 | 455 | 0.1% | |
| 47 | 443 | 444 | 0.3% | |
| 46 | 432 | 434 | 0.5% | |
| 45 | 421 | 424 | 0.7% | |
| 44 | 409 | 414 | 1.2% | |
| 43 | 400 | 404 | 1.0% | |
| 42 | 390 | 394 | 1.1% | |
| 41 | 381 | 385 | 0.9% | |
| 40 | 371 | 375 | 1.1% | |
| 39 | 362 | 366 | 1.0% | |
| 38 | 353 | 356 | 0.9% | |
| 37 | 344 | 347 | 0.9% | |
| 36 | 336 | 338 | 0.6% | |
| 35 | 327 | 329 | 0.6% | |
| 34 | 319 | 320 | 0.4% | |
| 33 | 311 | 312 | 0.2% | |
| 32 | 301 | 303 | 0.7% | |
| 31 | 294 | 295 | 0.2% | |
| 30 | 286 | 286 | 0.1% | |
| 29 | 279 | 278 | 0.3% | |
| 28 | 271 | 270 | 0.3% | |
| 27 | 264 | 262 | 0.6% | |
| 26 | 258 | 258 | 0.1% | BHN = 156+HRC1.42 HRC = 1.42√[BHN-156] |
| 25 | 253 | 253 | 0.1% | |
| 24 | 247 | 248 | 0.2% | |
| 23 | 243 | 242 | 0.4% | |
| 22 | 237 | 237 | 0.2% | |
| 21 | 231 | 231 | 0.1% | |
| 20 | 226 | 226 | 0.0% |
Brinell Hardness Number - Hultgren (BHN-H) ⁽⁴⁾
.png)
Rockwell C vs Brinell (Hultgren)
A spherical ball manufactured from Axel Gustaf Emanuel Hultgren's tungsten steel, which has since become known as Hultgren steel, will flatten less than a standard hardened steel ball and is used for the Brinell hardness test on materials with a BHN value of up to 500.
The following table is based upon a 10mm diameter ball and a force of 3000kg
| HRC | BHN-H | BHN-H {Q} | Error | Formulas |
|---|---|---|---|---|
| 60 | 613 | 613 | 0.0% | BHN = 70+HRC1.538 HRC = 1.538√[BHN-70] |
| 59 | 599 | 599 | 0.0% | |
| 58 | 587 | 585 | 0.3% | |
| 57 | 575 | 572 | 0.6% | |
| 56 | 561 | 558 | 0.5% | |
| 55 | 546 | 545 | 0.2% | |
| 54 | 534 | 532 | 0.4% | |
| 53 | 519 | 519 | 0.1% | |
| 52 | 508 | 506 | 0.4% | |
| 51 | 494 | 493 | 0.2% | |
| 50 | 481 | 480 | 0.2% | |
| 49 | 469 | 468 | 0.3% | |
| 48 | 455 | 455 | 0.1% | |
| 47 | 443 | 443 | 0.0% | |
| 46 | 432 | 431 | 0.3% | |
| 45 | 421 | 419 | 0.5% | |
| 44 | 409 | 409 | 0.0% | BHN = 129+HRC1.489 HRC = 1.489√[BHN-129] |
| 43 | 400 | 400 | 0.1% | |
| 42 | 390 | 390 | 0.1% | |
| 41 | 381 | 381 | 0.0% | |
| 40 | 371 | 372 | 0.2% | |
| 39 | 362 | 363 | 0.3% | |
| 38 | 353 | 354 | 0.3% | |
| 37 | 344 | 345 | 0.4% | |
| 36 | 336 | 337 | 0.2% | |
| 35 | 327 | 328 | 0.3% | |
| 34 | 319 | 320 | 0.2% | |
| 33 | 311 | 311 | 0.1% | |
| 32 | 301 | 303 | 0.7% | |
| 31 | 294 | 295 | 0.4% | |
| 30 | 286 | 287 | 0.4% | |
| 29 | 279 | 279 | 0.2% | |
| 28 | 271 | 272 | 0.3% | |
| 27 | 264 | 264 | 0.1% | |
| 26 | 258 | 257 | 0.4% | |
| 25 | 253 | 253 | 0.1% | BHN = 153.4+HRC1.43 HRC = 1.43√[BHN-153.4] |
| 24 | 247 | 248 | 0.2% | |
| 23 | 243 | 242 | 0.4% | |
| 22 | 237 | 237 | 0.2% | |
| 21 | 231 | 231 | 0.1% | |
| 20 | 226 | 226 | 0.0% |
Brinell Hardness Number - tungsten (BHN-W)
.png)
Rockwell C vs Brinell (tungsten) ⁽⁴⁾
A spherical ball manufactured from tungsten carbide will flatten less than standard or Hultgren balls and is used for hard materials with a BHN value of up to 630.
Whilst tungsten carbide balls may need to be smaller than steel balls (10mm) the accuracy of this test remains maximised by using the largest ball available. Therefore, even for very hard materials it is advisable to use a 10mm tungsten carbide ball where possible along with a suitably high load.
The following table is based upon a 10mm diameter ball and a force of 3000kg
| HRC | BHN-W | BHN-W {Q} | Error | Formulas |
|---|---|---|---|---|
| 65 | 739 | 743 | 0.5% | BHN = HRC1.593-30 HRC = 1.593√[BHN+30] |
| 64 | 722 | 724 | 0.2% | |
| 63 | 705 | 705 | 0.0% | |
| 62 | 688 | 687 | 0.2% | |
| 61 | 670 | 668 | 0.3% | |
| 60 | 654 | 650 | 0.6% | |
| 59 | 634 | 632 | 0.3% | |
| 58 | 615 | 614 | 0.1% | |
| 57 | 595 | 597 | 0.3% | |
| 56 | 577 | 579 | 0.4% | |
| 55 | 560 | 562 | 0.4% | |
| 54 | 543 | 545 | 0.4% | |
| 53 | 525 | 528 | 0.6% | |
| 52 | 512 | 511 | 0.1% | |
| 51 | 496 | 495 | 0.2% | |
| 50 | 481 | 479 | 0.5% | |
| 49 | 469 | 468 | 0.2% | BHN = 110+HRC1.511 HRC = 1.511√[BHN-110] |
| 48 | 455 | 457 | 0.4% | |
| 47 | 443 | 446 | 0.7% | |
| 46 | 432 | 435 | 0.8% | |
| 45 | 421 | 425 | 0.9% | |
| 44 | 409 | 414 | 1.3% | |
| 43 | 400 | 404 | 1.0% | |
| 42 | 390 | 394 | 0.9% | |
| 41 | 381 | 383 | 0.6% | |
| 40 | 371 | 373 | 0.7% | |
| 39 | 362 | 364 | 0.4% | |
| 38 | 353 | 354 | 0.2% | |
| 37 | 344 | 344 | 0.1% | |
| 36 | 336 | 335 | 0.4% | |
| 35 | 327 | 325 | 0.5% | |
| 34 | 319 | 316 | 0.8% | BHN = 143+HRC1.462 HRC = 1.462√[BHN-143] |
| 33 | 311 | 309 | 0.6% | |
| 32 | 301 | 302 | 0.2% | |
| 31 | 294 | 294 | 0.2% | |
| 30 | 286 | 287 | 0.5% | |
| 29 | 279 | 280 | 0.5% | |
| 28 | 271 | 274 | 0.9% | |
| 27 | 264 | 267 | 1.1% | |
| 26 | 258 | 260 | 0.8% | |
| 25 | 253 | 254 | 0.2% | |
| 24 | 247 | 247 | 0.1% | |
| 23 | 243 | 241 | 0.9% | |
| 22 | 237 | 235 | 0.9% | |
| 21 | 231 | 229 | 1.0% | |
| 20 | 226 | 223 | 1.4% |
Rockwell Hardness Number - A (HRA)
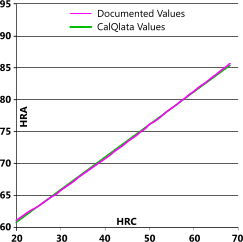
Rockwell C vs Rockwell A
The Rockwell A grade is suitable for extremely hard materials such as tungsten carbides, hardened high carbon steels and ceramics. It is also used for hard thin metal sheets.
The following table is based upon a diamond indenter and a force of 60kg
| HRC | HRA | HRA {Q} | Error | Formulas |
|---|---|---|---|---|
| 68 | 85.6 | 85 | 0.4% | HRA = 49.742+0.5229xHRC HRC = (HRA-49.742)÷0.5229 |
| 67 | 85 | 85 | 0.3% | |
| 66 | 84.5 | 84 | 0.3% | |
| 65 | 83.9 | 84 | 0.2% | |
| 64 | 83.4 | 83 | 0.2% | |
| 63 | 82.8 | 83 | 0.1% | |
| 62 | 82.3 | 82 | 0.2% | |
| 61 | 81.8 | 82 | 0.2% | |
| 60 | 81.2 | 81 | 0.1% | |
| 59 | 80.7 | 81 | 0.1% | |
| 58 | 80.1 | 80 | 0.0% | |
| 57 | 79.6 | 80 | 0.1% | |
| 56 | 79 | 79 | 0.0% | |
| 55 | 78.5 | 79 | 0.0% | |
| 54 | 78 | 78 | 0.0% | |
| 53 | 77.4 | 77 | 0.1% | |
| 52 | 76.8 | 77 | 0.2% | |
| 51 | 76.3 | 76 | 0.1% | |
| 50 | 75.9 | 76 | 0.0% | |
| 49 | 75.2 | 75 | 0.2% | |
| 48 | 74.7 | 75 | 0.2% | |
| 47 | 74.1 | 74 | 0.3% | |
| 46 | 73.6 | 74 | 0.3% | |
| 45 | 73.1 | 73 | 0.2% | |
| 44 | 72.5 | 73 | 0.3% | |
| 43 | 72 | 72 | 0.3% | |
| 42 | 71.5 | 72 | 0.3% | |
| 41 | 70.9 | 71 | 0.4% | |
| 40 | 70.4 | 71 | 0.4% | |
| 39 | 69.9 | 70 | 0.3% | |
| 38 | 69.4 | 70 | 0.3% | |
| 37 | 68.9 | 69 | 0.3% | |
| 36 | 68.4 | 69 | 0.2% | |
| 35 | 67.9 | 68 | 0.2% | |
| 34 | 67.4 | 68 | 0.2% | |
| 33 | 66.8 | 67 | 0.3% | |
| 32 | 66.3 | 66 | 0.3% | |
| 31 | 65.8 | 66 | 0.2% | |
| 30 | 65.3 | 65 | 0.2% | |
| 29 | 64.7 | 65 | 0.3% | |
| 28 | 64.3 | 64 | 0.1% | |
| 27 | 63.8 | 64 | 0.1% | |
| 26 | 63.3 | 63 | 0.1% | |
| 25 | 62.8 | 63 | 0.0% | |
| 24 | 62.4 | 62 | 0.2% | |
| 23 | 62 | 62 | 0.4% | |
| 22 | 61.5 | 61 | 0.4% | |
| 21 | 61 | 61 | 0.5% | |
| 20 | 60.5 | 60 | 0.5% |
Rockwell Hardness Number - B (HRB)
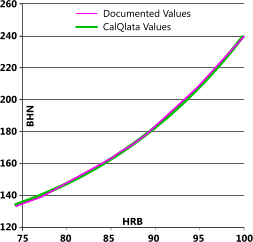
Rockwell B vs Brinell (std)
The same operational method as for the 'A' scale (see above) but this test applies to softer materials, such as low carbon steels, or steels in annealed condition and soft metals that fall below or around the lower end of the Rockwell 'C' Scale (i.e. less than 300).
A comparison is carried out using the standard Brinell test ball of 10mm and a 3000kg applied load (see BHN above) in order to facilitate a conversion with other hardness measurement systems.
| HRB | BHN | BHN {Q} | Error | Formulas |
|---|---|---|---|---|
| 100 | 240 | 240.6 | 0.3% | BHN = 96+1.051HRB HRB = Log1.051(BHN-96) |
| 99 | 234 | 233.6 | 0.2% | |
| 98 | 228 | 226.9 | 0.5% | |
| 97 | 222 | 220.6 | 0.6% | |
| 96 | 216 | 214.5 | 0.7% | |
| 95 | 210 | 208.8 | 0.6% | |
| 94 | 205 | 203.3 | 0.8% | |
| 93 | 200 | 198.1 | 0.9% | |
| 92 | 195 | 193.2 | 0.9% | |
| 91 | 190 | 188.4 | 0.8% | |
| 90 | 185 | 184.0 | 0.6% | |
| 89 | 180 | 179.7 | 0.2% | |
| 88 | 176 | 175.6 | 0.2% | |
| 87 | 172 | 171.8 | 0.1% | |
| 86 | 169 | 168.1 | 0.5% | |
| 85 | 165 | 164.6 | 0.3% | |
| 84 | 162 | 161.3 | 0.5% | |
| 83 | 159 | 158.1 | 0.6% | |
| 82 | 156 | 155.1 | 0.6% | |
| 81 | 153 | 152.2 | 0.5% | |
| 80 | 150 | 149.5 | 0.3% | |
| 79 | 147 | 146.9 | 0.1% | |
| 78 | 144 | 144.4 | 0.3% | |
| 77 | 141 | 142.1 | 0.8% | |
| 76 | 139 | 139.8 | 0.6% | |
| 75 | 137 | 137.7 | 0.5% | |
| 74 | 135 | 135.7 | 0.5% |
Rockwell Hardness Number - D (HRD)
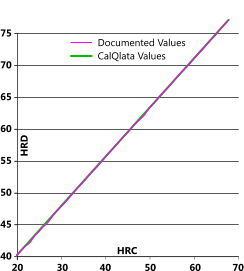
Rockwell C vs Rockwell D
The Rockwell D grade is for case hardened materials that need a lighter load than the C-Grade test but is otherwise identical.
The following table is based upon a diamond indenter and a force of 100kg
| HRC | HRD | HRD {Q} | Error | Formulas |
|---|---|---|---|---|
| 68 | 76.9 | 77 | 0.0% | HRD = 24.767+0.7667xHRC HRC = (HRD-24.767)÷0.7667 |
| 67 | 76.1 | 76 | 0.0% | |
| 66 | 75.4 | 75 | 0.0% | |
| 65 | 74.5 | 75 | 0.1% | |
| 64 | 73.8 | 74 | 0.0% | |
| 63 | 73 | 73 | 0.1% | |
| 62 | 72.2 | 72 | 0.1% | |
| 61 | 71.5 | 72 | 0.0% | |
| 60 | 70.7 | 71 | 0.1% | |
| 59 | 69.9 | 70 | 0.1% | |
| 58 | 69.2 | 69 | 0.1% | |
| 57 | 68.5 | 68 | 0.0% | |
| 56 | 67.7 | 68 | 0.0% | |
| 55 | 66.9 | 67 | 0.1% | |
| 54 | 66.1 | 66 | 0.1% | |
| 53 | 65.4 | 65 | 0.0% | |
| 52 | 64.6 | 65 | 0.1% | |
| 51 | 63.8 | 64 | 0.1% | |
| 50 | 63.1 | 63 | 0.0% | |
| 49 | 62.1 | 62 | 0.4% | |
| 48 | 61.4 | 62 | 0.3% | |
| 47 | 60.8 | 61 | 0.0% | |
| 46 | 60 | 60 | 0.1% | |
| 45 | 59.2 | 59 | 0.1% | |
| 44 | 58.5 | 59 | 0.0% | |
| 43 | 57.7 | 58 | 0.1% | |
| 42 | 56.9 | 57 | 0.1% | |
| 41 | 56.2 | 56 | 0.0% | |
| 40 | 55.4 | 55 | 0.1% | |
| 39 | 54.6 | 55 | 0.1% | |
| 38 | 53.8 | 54 | 0.2% | |
| 37 | 53.1 | 53 | 0.1% | |
| 36 | 52.3 | 52 | 0.1% | |
| 35 | 51.5 | 52 | 0.2% | |
| 34 | 50.8 | 51 | 0.1% | |
| 33 | 50 | 50 | 0.1% | |
| 32 | 49.2 | 49 | 0.2% | |
| 31 | 48.4 | 49 | 0.3% | |
| 30 | 47.7 | 48 | 0.1% | |
| 29 | 47 | 47 | 0.0% | |
| 28 | 46.1 | 46 | 0.3% | |
| 27 | 45.2 | 45 | 0.6% | |
| 26 | 44.6 | 45 | 0.2% | |
| 25 | 43.8 | 44 | 0.3% | |
| 24 | 43.1 | 43 | 0.2% | |
| 23 | 42.1 | 42 | 0.7% | |
| 22 | 41.6 | 42 | 0.1% | |
| 21 | 40.9 | 41 | 0.1% | |
| 20 | 40.1 | 40 | 0.0% |
Rockwell Hardness Number - 15-15N (HR15) ⁽⁵⁾⁽⁶⁾
.png)
Rockwell C vs Rockwell 15-15
The same operational method as for the A, B, C & D ranges applies to this hardness range but uses the '15' scale and a 15kg load.
This scale is used for materials that will result in very small indentations such as very hard materials, the harder the material the greater the load (i.e. 30kg or 45kg see below).
The following table is based upon a diamond indenter, a force of 15kg and the 'N' sub-scale
| HRC | HR15 | HR15 {Q} | Error | Formulas |
|---|---|---|---|---|
| 68 | 93.2 | 93 | 0.1% | HR15 = 61.5+HRC0.82 HRC = 0.82√[HR15-61.5] |
| 67 | 92.9 | 93 | 0.0% | |
| 66 | 92.5 | 93 | 0.1% | |
| 65 | 92.2 | 92 | 0.0% | |
| 64 | 91.8 | 92 | 0.0% | |
| 63 | 91.4 | 91 | 0.0% | |
| 62 | 91.1 | 91 | 0.1% | |
| 61 | 90.7 | 91 | 0.1% | |
| 60 | 90.2 | 90 | 0.0% | |
| 59 | 89.8 | 90 | 0.2% | HR15 = 56+HRC0.865 HRC = 0.865√[HR15-56] |
| 58 | 89.3 | 90 | 0.3% | |
| 57 | 88.9 | 89 | 0.1% | |
| 56 | 88.3 | 89 | 0.3% | |
| 55 | 87.9 | 88 | 0.1% | |
| 54 | 87.4 | 88 | 0.1% | |
| 53 | 86.9 | 87 | 0.1% | |
| 52 | 86.4 | 87 | 0.1% | |
| 51 | 85.9 | 86 | 0.1% | |
| 50 | 85.5 | 85 | 0.0% | |
| 49 | 85 | 85 | 0.0% | |
| 48 | 84.5 | 84 | 0.0% | |
| 47 | 83.9 | 84 | 0.1% | |
| 46 | 83.5 | 83 | 0.1% | |
| 45 | 83 | 83 | 0.1% | |
| 44 | 82.5 | 82 | 0.1% | |
| 43 | 82 | 82 | 0.1% | |
| 42 | 81.5 | 81 | 0.2% | |
| 41 | 80.9 | 81 | 0.1% | |
| 40 | 80.4 | 80 | 0.1% | |
| 39 | 79.9 | 80 | 0.1% | |
| 38 | 79.4 | 79 | 0.2% | |
| 37 | 78.8 | 79 | 0.1% | |
| 36 | 78.3 | 78 | 0.1% | |
| 35 | 77.7 | 78 | 0.1% | |
| 34 | 77.2 | 77 | 0.1% | |
| 33 | 76.6 | 77 | 0.0% | |
| 32 | 76.1 | 76 | 0.1% | |
| 31 | 75.6 | 75 | 0.1% | |
| 30 | 75 | 75 | 0.1% | |
| 29 | 74.5 | 74 | 0.1% | |
| 28 | 73.9 | 74 | 0.1% | |
| 27 | 73.3 | 73 | 0.0% | |
| 26 | 72.8 | 73 | 0.1% | |
| 25 | 72.2 | 72 | 0.0% | |
| 24 | 71.6 | 72 | 0.0% | |
| 23 | 71 | 71 | 0.1% | |
| 22 | 70.5 | 70 | 0.0% | |
| 21 | 69.9 | 70 | 0.0% | |
| 20 | 69.4 | 69 | 0.1% |
Rockwell Hardness Number - 30-30N (HR30) ⁽⁵⁾⁽⁶⁾
.png)
Rockwell C vs Rockwell 30-30
The same operational method as for the '15' scale (see above) but uses the '30' scale and a 30kg load.
This scale is used for materials that will result in very small indentations such as very hard materials, the harder the material the greater the load (i.e. 15kg see above or 45kg see below).
The following table is based upon a diamond indenter, a force of 30kg and the 'N' sub-scale
| HRC | HR30 | HR30 {Q} | Error | Formulas |
|---|---|---|---|---|
| 68 | 84.4 | 85 | 0.2% | HR30 = 22.6+HRC0.978 HRC = 0.978√[HR30-22.6] |
| 67 | 83.6 | 84 | 0.1% | |
| 66 | 82.8 | 83 | 0.0% | |
| 65 | 81.9 | 82 | 0.0% | |
| 64 | 81.1 | 81 | 0.1% | |
| 63 | 80.1 | 80 | 0.0% | |
| 62 | 79.3 | 79 | 0.1% | |
| 61 | 78.4 | 78 | 0.1% | |
| 60 | 77.5 | 77 | 0.1% | |
| 59 | 76.6 | 77 | 0.1% | |
| 58 | 75.7 | 76 | 0.1% | |
| 57 | 74.8 | 75 | 0.1% | |
| 56 | 73.9 | 74 | 0.1% | |
| 55 | 73 | 73 | 0.1% | |
| 54 | 72 | 72 | 0.1% | |
| 53 | 71.2 | 71 | 0.0% | |
| 52 | 70.2 | 70 | 0.1% | |
| 51 | 69.4 | 69 | 0.0% | |
| 50 | 68.5 | 68 | 0.0% | |
| 49 | 67.6 | 68 | 0.0% | |
| 48 | 66.7 | 67 | 0.0% | |
| 47 | 65.8 | 66 | 0.0% | |
| 46 | 64.8 | 65 | 0.1% | |
| 45 | 64 | 64 | 0.0% | |
| 44 | 63.1 | 63 | 0.0% | |
| 43 | 62.2 | 62 | 0.0% | |
| 42 | 61.3 | 61 | 0.0% | |
| 41 | 60.4 | 60 | 0.0% | |
| 40 | 59.5 | 59 | 0.0% | |
| 39 | 58.6 | 59 | 0.0% | |
| 38 | 57.7 | 58 | 0.0% | |
| 37 | 56.8 | 57 | 0.0% | |
| 36 | 55.9 | 56 | 0.1% | |
| 35 | 55 | 55 | 0.1% | |
| 34 | 54.2 | 54 | 0.3% | |
| 33 | 53.3 | 53 | 0.3% | |
| 32 | 52.1 | 52 | 0.3% | |
| 31 | 51.3 | 51 | 0.1% | |
| 30 | 50.4 | 50 | 0.1% | |
| 29 | 49.5 | 50 | 0.1% | |
| 28 | 48.6 | 49 | 0.0% | |
| 27 | 47.7 | 48 | 0.0% | |
| 26 | 46.8 | 47 | 0.0% | |
| 25 | 45.9 | 46 | 0.0% | |
| 24 | 45 | 45 | 0.0% | |
| 23 | 44 | 44 | 0.2% | |
| 22 | 43.2 | 43 | 0.1% | |
| 21 | 42.3 | 42 | 0.1% | |
| 20 | 41.5 | 41 | 0.4% |
Rockwell Hardness Number - 45-45N (HR45) ⁽⁵⁾⁽⁶⁾
.png)
Rockwell C vs Rockwell 45-45
The same operational method as for the '15' scale (see above) but uses the '45' scale and a 45kg load.
This scale is used for materials that will result in very small indentations such as very hard materials, the harder the material the greater the load (i.e. 30kg or 45kg see above).
The following table is based upon a diamond indenter, a force of 45kg and the 'N' sub-scale
| HRC | HR45 | HR45 {Q} | Error | Formulas |
|---|---|---|---|---|
| 68 | 75.4 | 75 | 0.1% | HR45 = 0.86+HRC1.022 HRC = 1.022√[HR45-0.86] |
| 67 | 74.2 | 74 | 0.2% | |
| 66 | 73.3 | 73 | 0.1% | |
| 65 | 72 | 72 | 0.2% | |
| 64 | 71 | 71 | 0.0% | |
| 63 | 69.9 | 70 | 0.0% | |
| 62 | 68.8 | 69 | 0.1% | |
| 61 | 67.7 | 68 | 0.1% | |
| 60 | 66.6 | 67 | 0.1% | |
| 59 | 65.5 | 65 | 0.2% | |
| 58 | 64.3 | 64 | 0.0% | |
| 57 | 63.2 | 63 | 0.1% | |
| 56 | 62 | 62 | 0.1% | |
| 55 | 60.9 | 61 | 0.0% | |
| 54 | 59.8 | 60 | 0.3% | HR45 = HRC1.038-2.85 HRC = 1.038√[HR45+2.85] |
| 53 | 58.6 | 59 | 0.3% | |
| 52 | 57.4 | 58 | 0.3% | |
| 51 | 56.1 | 56 | 0.5% | |
| 50 | 55 | 55 | 0.3% | |
| 49 | 53.8 | 54 | 0.3% | |
| 48 | 52.5 | 53 | 0.5% | |
| 47 | 51.4 | 52 | 0.3% | |
| 46 | 50.3 | 50 | 0.1% | |
| 45 | 49 | 49 | 0.3% | |
| 44 | 47.8 | 48 | 0.3% | |
| 43 | 46.7 | 47 | 0.1% | |
| 42 | 45.5 | 46 | 0.1% | |
| 41 | 44.3 | 44 | 0.1% | |
| 40 | 43.1 | 43 | 0.2% | |
| 39 | 41.9 | 42 | 0.2% | |
| 38 | 40.8 | 41 | 0.0% | |
| 37 | 39.6 | 40 | 0.0% | |
| 36 | 38.4 | 38 | 0.0% | |
| 35 | 37.2 | 37 | 0.0% | |
| 34 | 36.1 | 36 | 0.2% | |
| 33 | 34.9 | 35 | 0.2% | |
| 32 | 33.7 | 34 | 0.1% | |
| 31 | 32.5 | 32 | 0.1% | |
| 30 | 31.3 | 31 | 0.0% | |
| 29 | 30.1 | 30 | 0.0% | |
| 28 | 28.9 | 29 | 0.1% | |
| 27 | 27.8 | 28 | 0.2% | |
| 26 | 26.7 | 27 | 0.5% | |
| 25 | 25.5 | 25 | 0.4% | |
| 24 | 24.3 | 24 | 0.3% | |
| 23 | 23.1 | 23 | 0.2% | |
| 22 | 22 | 22 | 0.5% | |
| 21 | 20.7 | 21 | 0.1% | |
| 20 | 19.6 | 20 | 0.2% |
Shore Hardness Number (SHN)
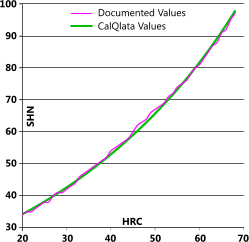
Rockwell C vs Shore
The Shore Scleroscope (or durometer) was developed by Albert F. Shore (USA) and uses a small diamond tipped hammer weighing 1/12th of an ounce (2.36246g) in a graduated glass tube to measure the hardness of a material. The hammer is dropped from a predefined height and the measured rebound height defines the hardness of the impacted material.
This is a simple system that requires no calculation and no complicated equipment. Whilst it is not considered as accurate as the other hardness testing methods, this is only because its operation is prone to misuse. However, if correctly used and read, this method should be at least as accurate as any other.
This equipment has the added advantage of being practical to transport and use in any environment, but works best on hard materials, i.e. the results for materials such as lead will be unreliable as the rebound height will be virtually non-existent.
The greater than expected errors in the calculated results are due to the erratic nature of the documented values (see image) which, if measured accurately should follow a much smoother curve. The curve generated by the formulas (SHN {Q}) is considered (by CalQlata) to be more representative of the actual Shore values than the documented values (SHN).
| HRC | SHN | SHN {Q} | Error | Formulas |
|---|---|---|---|---|
| 68 | 97 | 97 | 0.5% | SHN = 201.5 - 1½.√[ 125² - (36+HRC)² ] HRC = √[ 125² - ((201.5-SHN) / 1½)²] - 36 |
| 67 | 95 | 95 | 0.3% | |
| 66 | 92 | 93 | 1.2% | |
| 65 | 91 | 91 | 0.0% | |
| 64 | 88 | 89 | 1.1% | |
| 63 | 87 | 87 | 0.0% | |
| 62 | 85 | 85 | 0.1% | |
| 61 | 83 | 83 | 0.3% | |
| 60 | 81 | 81 | 0.5% | |
| 59 | 80 | 80 | 0.5% | |
| 58 | 78 | 78 | 0.1% | |
| 57 | 76 | 76 | 0.3% | |
| 56 | 75 | 75 | 0.6% | |
| 55 | 74 | 73 | 1.4% | |
| 54 | 72 | 71 | 0.9% | |
| 53 | 71 | 70 | 1.6% | |
| 52 | 69 | 68 | 1.0% | |
| 51 | 68 | 67 | 1.7% | |
| 50 | 67 | 65 | 2.3% | |
| 49 | 66 | 64 | 3.0% | |
| 48 | 64 | 63 | 2.1% | |
| 47 | 63 | 61 | 2.7% | |
| 46 | 62 | 60 | 3.3% | |
| 45 | 60 | 59 | 2.2% | |
| 44 | 58 | 57 | 1.0% | |
| 43 | 57 | 56 | 1.4% | |
| 42 | 56 | 55 | 1.8% | |
| 41 | 55 | 54 | 2.2% | |
| 40 | 54 | 53 | 2.5% | |
| 39 | 52 | 52 | 1.0% | |
| 38 | 51 | 50 | 1.2% | |
| 37 | 50 | 49 | 1.4% | |
| 36 | 49 | 48 | 1.6% | |
| 35 | 48 | 47 | 1.7% | |
| 34 | 47 | 46 | 1.8% | |
| 33 | 46 | 45 | 1.8% | |
| 32 | 44 | 44 | 0.4% | |
| 31 | 43 | 43 | 0.5% | |
| 30 | 42 | 42 | 0.6% | |
| 29 | 41 | 41 | 0.8% | |
| 28 | 41 | 40 | 1.4% | |
| 27 | 40 | 40 | 1.1% | |
| 26 | 38 | 39 | 1.8% | |
| 25 | 38 | 38 | 0.4% | |
| 24 | 37 | 37 | 0.0% | |
| 23 | 36 | 36 | 0.6% | |
| 22 | 35 | 35 | 1.2% | |
| 21 | 35 | 35 | 1.1% | |
| 20 | 34 | 34 | 0.4% |
Comparison Charts
HRC: The common comparison hardness range of values (Rockwell C). Values below 20 are ignored as their reliability varies too much between test methods.
e.g. SHN: The comparable hardness range from a documented source⁽²⁾; Brinell, Vickers, Shore, etc.
e.g. SHN {Q}: The comparable range of values calculated using the formulas in the right-hand column. The graph immediately above each Table is a plot of the documented values compared with the calculated values.
Error: The percentage difference between documented and calculated values using the formulas in the right-hand column.
Formulas: The formulas used to calculate the Q values⁽³⁾.
Notes
- Except for the 'Vickers' formula which can be found in numerous sources; e.g. https://link.springer.com/article/10.1007%2FBF02833189#page-2
- Reference publication 2 (see Further Reading below)
- These formulas have been devised by CalQlata
- The same operating conditions and calculation methods are used for this test as for the Brinell standard test (see above).
- Two sub-scales are provided: N & T
N is for very hard materials that will result in a small indentation
T is for softer materials to minimise the indentation - The hardness values are comparable with both the above sub-scales in that any given material would show the same hardness value irrespective of the sub-scale used. Each scale, however, is better suited, and therefore more accurate and reliable if used with the appropriate materials.
Further Reading
You will find further reading on this subject in reference publications(2, 3 & 44)